斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

• 0 <= n <= 30

题解:

这个题是简单的计算斐波那契数列，斐波那契数列就是， 1， 1， 2， 3， 5， 8。。。。这样的数列，从第二个开始，每个数都是它前面两个数的和。本文介绍这题的三种不同时间复杂度的解法，分别是递归实现O(n^2)，迭代实现O(n)，矩阵乘法实现O(logn)。

递归实现

这个就比较简单了，直接上代码，算法的复杂度是O(n^2)

public static int fib(int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}return fib(n - 1) + fib(n - 2);
}

迭代实现

算法时间复杂度是O(n)，和递归实现的区别是，总是记录了前两个值，相当于记忆性递归的效果。

代码如下：

public static int fib(int n) {if (n == 0) {return 0;}if (n == 1) {return 1;}// f(n - 1)int fn1 = 1;// f(n - 2)int fn2 = 0;int res = fn2 + fn1;for (int i = 3; i <= n; i++) {fn2 = fn1;fn1 = res;res = fn1 + fn2;}return res;
}

矩阵乘法实现

算法的时间复杂度是O(logn)。

首先引入矩阵相乘$$(\begin{array}{cc}{F}_n& F_{n-1}\\ F_{n-1}& F_{n-2}\end{array})\ast (\begin{array}{cc}1& 1\\ 1& 0\end{array})=(\begin{array}{cc}{F}_n+Fn-1& F_n\\ F_{n-1}+F_{n-2}& F_{n-1}\end{array})$$

根据斐波那契迭代的公式可以推得

• $$F_n+F_{n-1}=F_{n+1}$$
• $$F_n=F_n$$
• $$F_{n-1}+F_{n-2}=F_n$$
• $$F_{n-1}=F_{n-1}$$

由此可以得出结论。

$$A_n\ast (\begin{array}{cc}1& 1\\ 1& 0\end{array})=(A_{n+1})$$

只需要记录第n-1项，第n-2项，第n项，就可以使用乘法的方法来计算出第n+1项。

根据上式得到最终递推式如下：

$$A_n={(\begin{array}{cc}1& 1\\ 1& 0\end{array})}^{n-1}$$

到了这一步，直接使用矩阵乘法来计算的话，最终的时间复杂度为O(n)。但是乘法的话存在快速幂运算的计算方法，使用快速幂运算，可以将运算的时间复杂度进一步降低。

快速幂运算逻辑如下：

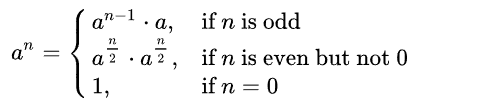
计算a的n次方，如果a是偶数，那就直接计算$$a^{n/2}\ast a^{n/2}$$，如果是奇数就计算a乘上$$a^{n-1}$$。

代码如下：

public static int fib(int n) {if (n == 0) {return 0;} else if (n == 1) {return 1;}int[][] matrix = new int[][]{{1, 1},{1, 0}};matrix = powerMatrix(matrix, n - 1);return matrix[0][0];
}public static int[][] powerMatrix(int[][] matrix, int n) {if (n <= 1) {return matrix;} else if (n % 2 == 0){matrix = powerMatrix(matrix, n / 2);matrix = matrixMul(matrix, matrix);return matrix;} else {return matrixMul(matrix, Objects.requireNonNull(powerMatrix(matrix, n - 1)));}
}public static int[][] matrixMul(int[][] m1, int[][] m2) {int ROWS = m1.length;int COLS = m2[0].length;int[][] res = new int[ROWS][COLS];for (int i = 0; i < ROWS; i++) {for (int j = 0; j < COLS; j++) {int sum = 0;for (int k = 0; k < m1[0].length; k++) {sum += m1[i][k] * m2[k][j];}res[i][j] = sum;}}return res;
}