理性人不选择坏战略

上一节，我们借助囚徒困境博弈阐述了什么是占优均衡。在囚徒困境中，无论别人采取什么行动，每一个参与人都有一个特定的最优选择（占优战略）。也就是说，一个理性的参与人在做决策时，并不需要假定对方也是理性的。对于这样的博弈，我们很容易预测它的结果。但是有些博弈可能是一方有占优战略，另一方没有占优战略，即什么是自己的最优行动依赖于他预测对方会选择什么行动，对方的选择不同，自己的最优行动就不同。此时博弈结果又会怎样呢？下面我们就用“智猪博弈”（boxed pigs game）来分析这个问题。

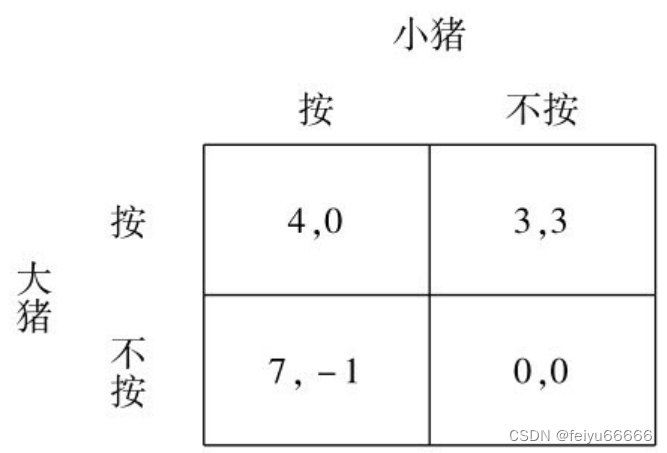
设想猪圈里有两头猪，一头大猪和一头小猪。在猪圈的一头装有一个按钮，另一头装有食槽。在这头按一下按钮，那头的食槽会有8单位的食物出现。但不管是大猪还是小猪，按动按钮都需要花2个单位食物的成本。如果两头猪一起按，各付2单位食物成本，然后大猪吃到6份食物，小猪可以吃到2份食物，扣除成本后，双方的净收益分别为4和0。如果大猪按、小猪不按，则小猪不付出任何代价就可以吃到3份，大猪按完之后跑回来可以吃到5份，扣除其按按钮的2个单位的成本，大猪的净收益也是3。反过来，如果大猪不按、小猪按的话，大猪可以不付出任何代价就可以吃到7份，小猪则只可以吃到1份，扣除其2单位的成本，则小猪的净收益为-1。如果两头猪都不按，则不付出成本，但也不会有食物吃，净收益都为0。如下图所示。

现在的问题是，谁来按这个按钮？

先考虑大猪的情况：如果小猪按的话，大猪的最优选择是“等待”（7＞4）；但如果小猪等待的话，大猪的最优选择是“按”（3＞0）。这就和前面所讲的囚徒困境博弈不一样了。在囚徒困境博弈中，每一个参与人都有一个占优战略——不论对方是否坦白，你最好是坦白。但在智猪博弈中，大猪没有占优战略，大猪的最优选择依赖于小猪的选择。所以大猪在做出选择前必须猜测小猪的选择。

那么，小猪会如何选择呢？对于小猪来说，如果大猪按，自己的最优选择是“不按”（3＞0）；如果大猪不按，自己的最优选择仍然“不按”（0＞-1）。这表明小猪选择“不按”是一个占优战略。

那大猪应该怎么办呢？我们前边假定的每一个博弈参与人（大猪或小猪）都是理性的，但并没有假定一方知道另一方也是理性的。显然，小猪在做决策时并不需要假定大猪是理性的，因为无论大猪是否理性，小猪的最优决策都是不按；但大猪的情况不同，即使小猪是理性的，如果大猪不知道小猪是否理性，大猪就没有办法做出选择。

为了预测这个博弈的结果，我们必须对大猪的理性程度做出进一步的假设。假定大猪不仅自己是理性的，也知道小猪是理性的。作为理性的参与人，小猪不会按。由于大猪知道小猪是理性的，就会知道小猪不会按，因此，大猪的最优选择只能是按。博弈的结局就是：大猪按，小猪不按，各得3单位的净报酬。

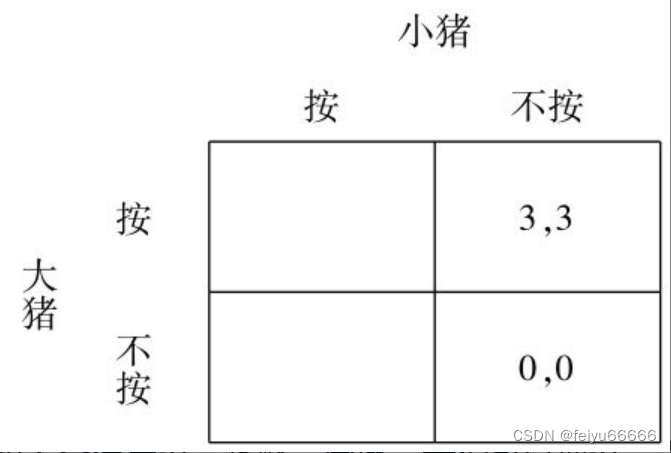
从这个例子里面，我们可以进一步提出一个概念——劣战略（dominated strategy）。所谓劣战略是指不论对手选择什么，自己都不会选择的战略。在智猪博弈中，对于参与人小猪来说，“按”就是它的一个劣战略。因为，无论大猪按还是不按，对于小猪，按都不是它的最好选择。因此，如果大猪知道小猪是理性的，就可以把“按”这一战略从小猪的战略集合中去掉。大猪现在面对的博弈如下图所示：

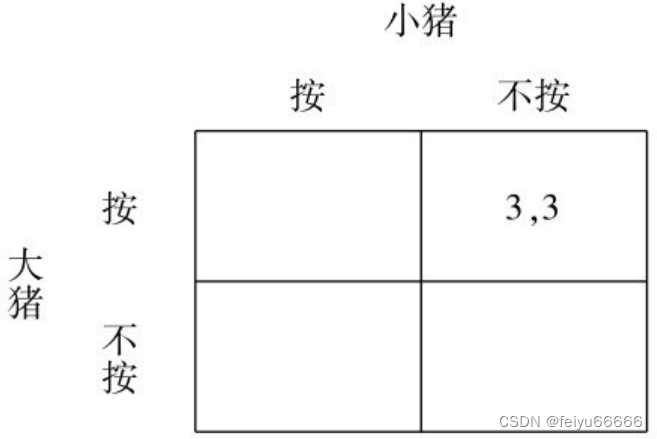
这时，对于大猪来说，“不按”也变成劣战略了，他也不会使用这一战略。因此，我们可以把这一劣战略再从大猪的战略集合中去掉，得到下图所示的结果：

这样一来，我们得到了唯一的最优战略组合是：大猪按，小猪不按。这就是大小猪博弈的战略均衡。寻找这个博弈的均衡的进程，是相继剔除劣战略的过程。所以，这个均衡被称为“重复剔除占优战略均衡”（iterated dominance equilibrium）。

批注：和“纳什均衡”的区别在哪里呀？

智猪博弈的均衡解在现实中有许多应用。比如说，股份公司中，股东承担着监督经理的职能，但股东中有大股东和小股东之分，他们从监督中得到的收益并不一样。监督经理需要搜集信息，花费时间。在监督成本相同的情况下，大股东从监督中得到的好处显然多于小股东。这里，大股东类似“大猪”，小股东类似“小猪”。均衡结果是，大股东担当起搜集信息、监督经理的责任，小股东则搭大股东的便车。股票市场上炒股票也是如此。股市上有庄家和散户。庄家类似“大猪”，散户类似“小猪”。这时候，“跟庄”是散户的最优选择，而庄家则必须自己搜集信息，进行分析。

市场中大企业与小企业之间的关系也存在类似的问题。进行研究开发，为新产品做广告，对大企业来说是值得的，对小企业来说则可能得不偿失。所以，大企业往往负责创新，而小企业把精力花在模仿上。

国际范围的反恐怖主义的活动也类似一个智猪博弈。在全球化时代，恐怖主义已成为一种国际现象，伤害所有的国家。但反恐的成本是很高的，小国尽管也不喜欢恐怖分子，但他们也没有积极性反恐。所以，国际反恐中，一定是大国承担更大的责任（人力、物力），小国搭便车。即大国扮演大猪的角色，小国扮演小猪的角色。随着中国的崛起，国际社会要求中国承担更大的责任，也是这个道理。国际反恐可以理解为国际范围的公共产品。前面讲公共产品的生产是一个囚徒困境博弈，事实上有些公共产品的生产类似智猪博弈，因为受益者是不对称的，有人受益大，有人受益小。在这种情况下，受益大的人可能有积极性私人生产公共产品，如过去农村一些大户人家就负责本村道路的维修。这也就是说，并不是所有的公共产品都需要政府提供。

社会改革中也有类似的情况。同样的改革给一部分人带来的好处可能比另一部分大得多。这时候，前一部分人比后一部分人更有积极性改革，改革往往就是由这些“大猪”推动的。如改革能创造出更多的“大猪”来，改革的速度就会加快。

理性作为共同知识

分析智猪博弈是一个重复剔除劣战略的过程。具体来说，首先在整个博弈当中，找出某一个参与人的劣战略，把它剔除掉；然后再在剩下的博弈中再找出劣战略并将其剔除；不断进行下去，如果剔除到最后只留下一个战略组合，那么这个战略组合就是我们说的重复剔除占优均衡。这种情况下，我们说这个博弈是重复剔除占优可解博弈。

我们已经看到，预测这样的博弈中每个人会选择什么，我们需要对参与人的理性程度做出更高的要求，仅仅假定每个参与人都是理性的并不能告诉我们均衡结果是怎样的。比如，在智猪博弈中，除了假定大猪和小猪都是理性的外，我们至少还得假定大猪知道小猪是理性的。小猪是理性的，意味着小猪不会选择按。但如果大猪不知道小猪是理性的，大猪仍然不知道如何选择。

但这个博弈对理性程度的要求仍然是很低的，我们甚至不需要假定小猪知道大猪是理性的，因为不论大猪是否理性，小猪都知道自己的最优选择是不按。在许多博弈中，即使假定每个参与人知道其他参与人是理性的，仍然不能告诉我们参与人会如何选择。

为此，我们需要引入理性共识（common knowledge of rationality）的概念，并定义零阶（zero-order）、一阶（first-order）、二阶（second-order），直至无限阶次的理性共识。零阶理性共识：每个人都是理性的，但不知道其他人是否理性；一阶理性共识：除了要求每个人都是理性的，还要求每个人都知道其他人是理性的；二阶理性共识则需要在满足一阶的基础上更进一步：首先每个人是理性的，同时每个人知道其他人是理性的，并且每个人知道其他人知道自己是理性的；依次类推，N阶理性共识，直至无穷阶次的理性共识。

一般讲的理性共识是无穷阶次的理性共识。打个比方，类似一个人前后各有一面镜子，镜子里有无穷个映像。这是博弈论中的一个基本假设，但现实很少达到，这是博弈分析的结果与现实有偏离的一个重要原因。生活中之所以有计谋，就是由于参与人不满足理性共识的要求，否则，博弈的结果是任何人都可以预测的，任何计谋都不可能得逞。比方说，乙很聪明，甲也知道乙很聪明，但是乙不知道甲知道乙很聪明，这种情况下，乙出个计谋骗甲，甲“将计就计”，最后获胜的反倒是甲。如果乙知道甲知道乙很聪明，乙就知道任何计谋都会被甲识破，乙就不可能有机会被“将计就计”。田忌赛马的故事中，齐王的上中下三匹马均好过田忌的上中下三匹马，但田忌用下马对齐王的上马，上马对齐王的中马，中马对齐王的下马，结果田忌以2∶1获胜。容易看出，田忌之所以能获胜，就是因为齐王不知道田忌聪明，或者说齐王太傻。如果齐王足够聪明的话，只要要求田忌先出马（齐王应该有这个权力），齐王一定可以3∶0获胜。

尽管很少有人能达到无穷阶理性共识，但像齐王这么“傻”的人也不多。为了说明理性共识在重复剔除中的重要性，考虑如下所示的博弈。在该博弈中，每个参与人都有四个选择，仍假定理性是共同知识。

首先看R的选择：如果C选择C1, R应该选择R1；如果C选C2，则R应该选择R2；类似地，C3、C4对应的最优反应分别是R3、R4。显然，R的任何一种选择都是理性的，具体依赖于他如何判断C的选择。

再来看C的选择：如果R选择R1, C会选择C3；如果R选择R2, C会选择C2。R3、R4对应的最优反应分别是C2、C1。

在这个博弈里，无论R选择什么，C都不会选择C4，即C4是C的劣战略。如果R知道C是理性的，R就不再会选择R4，因为R选择R4的唯一理由是C会选择C4，现在R知道理性的C不会选择C4，故也不会选择R4。

进一步，我们知道，C选择C1的唯一理由是R选择R4。如果现在C知道R不会选择R4, C就不会选择C1。所以可以进一步剔除C1。同样的道理，接下来，R会剔除R1。同理可以再依次剔除C3和R3。最后只剩下（C2, R2），双方的收益均为1，这就是前述讲到的重复剔除占优均衡。可以看到，重复剔除占优均衡的求解是根据理性共识一步一步地剔除劣战略，最后得到唯一的均衡结果。一般来说，博弈中参与人的选择越多，对理性共识的要求就越高。

实际上，求解这个均衡要求五阶理性共识：

零阶理性共识：C是理性的，这意味着他不会选择C4；

一阶理性共识：R知道C是理性的，这意味着他知道C不会选C4，故自己也不会选择R4；

二阶理性共识：C知道R知道C是理性的，这意味着C知道R将不会选R4，故自己不应该选择C1；

三阶理性共识：R知道C知道R知道C是理性的，这意味着R知道C不会选C1了，故自己不应该选择R1；

四阶理性共识：C知道R知道C知道R知道C是理性的，这意味着C现在知道R不会选R1了，故自己不应该选C3；

五阶理性共识：R知道C知道R知道C知道R知道C是理性的，这意味着R知道C不会选C3了，故自己不应该选R3。

经过上述推理，最后的结果将是R选择R2, C选择C2。

这样的一个推理过程可能让读者已经都晕倒了。这说明理性共识对于求解和预测一个博弈要求非常高，现实中参加博弈的参与人很难达到这一要求。这也是我们前面提到的很多时候博弈论的理论预测结果和现实中实际结果会有差异的一个主要原因。