【人工智能】八数码问题的A*搜索算法实现

一、实验要求

熟悉和掌握启发式搜索的定义、估价函数和算法过程，并利用A*算法求解八数码问题，理解求解流程和搜索顺序

二、实验原理

定义h*(n)为状态n到目的状态的最优路径的代价，则当A搜索算法的启发函数h(n)小于等于h* (n)，即满足

h(n)≤h*(n)

对所有结点n时，A搜索算法被称为A*搜索算法。

A* 搜索算法是由著名的人工智能学者Nilsson 提出的，它是目前最有影响的启发式图搜索算法，也称为最佳图搜索算法。

如果某一问题有解,那么利用A*搜索算法对该问题进行搜索则一定能搜索到解，并且一定能搜索到最优解。

A*算法有以下特性：可采纳性、单调性、信息性。

三、实验过程记录

八数码问题就是在一个3*3的方格盘上，放有1-8的数码，余下一格为空。空格四周上下左右的数码可移到空格。需要找到一个数码移动序列使初始的无序数码转变为一些特殊的排列。

我们下面的求解均以该题为例

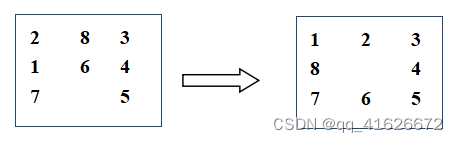
利用A*算法，首先需要给出估价函数f(n)。

已知f(n)=g(n)+h(n)，g(n)代表从初始节点到n节点的实际代价，h(n)代表从n节点到目的节点的最佳路径的估计代价。根据问题，我们定义g(n)=d(n)，即当前实际代价为状态的深度；h(n)=w(n)，估计最优代价为“不在位”的数码数量，且满足h(n)<=h*(n)。至此，A*算法所需准备完成。

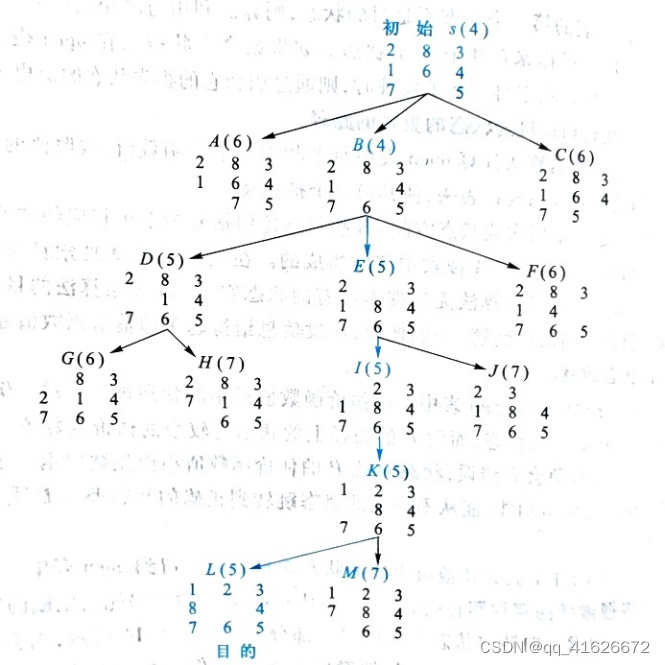
我们可以得到如下的搜索树，此时的s-B-E-I-K-L即为最优解路。

下面我们利用Python实现A*算法求解，程序源代码如下：

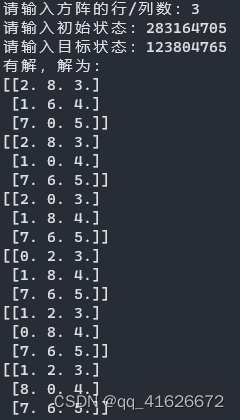
import numpy as npimport operatorO=int(input(("请输入方阵的行/列数：")))A=list(input("请输入初始状态："))B=list(input("请输入目标状态："))z=0M=np.zeros((O,O))N=np.zeros((O,O))for i in range(O):for j in range(O):M[i][j]=A[z]N[i][j]=B[z]z=z+1openlist=[]#open表class State:def __init__(self,m):self.node=m#节点代表的状态self.f=0#f(n)=g(n)+h(n)self.g=0#g(n)self.h=0#h(n)self.father=None#节点的父亲节点init = State(M)#初始状态goal = State(N)#目标状态#启发函数def h(s):a=0for i in range(len(s.node)):for j in range(len(s.node[i])):if s.node[i][j]!=goal.node[i][j]:a=a+1return a#对节点列表按照估价函数的值的规则排序def list_sort(l):cmp=operator.attrgetter('f')l.sort(key=cmp)#A*算法   def A_star(s):global openlist#全局变量可以让open表进行时时更新openlist=[s]while(openlist):#当open表不为空get=openlist[0] #取出open表的首节点 if (get.node==goal.node).all():#判断是否与目标节点一致return getopenlist.remove(get)#将get移出open表#判断此时状态的空格位置for a in range(len(get.node)):for b in range(len(get.node[a])):if get.node[a][b]==0:breakif get.node[a][b]==0:break#开始移动for i in range(len(get.node)):for j in range(len(get.node[i])):c=get.node.copy()if (i+j-a-b)**2==1:c[a][b]=c[i][j]c[i][j]=0new=State(c)new.father=get#此时取出的get节点成为新节点的父亲节点new.g=get.g+1#新节点与父亲节点的距离new.h=h(new)#新节点的启发函数值new.f=new.g+new.h#新节点的估价函数值openlist.append(new)#加入open表中list_sort(openlist)#排序# 递归打印路径def printpath(f):if f is None:return#注意print()语句放在递归调用前和递归调用后的区别。放在后实现了倒叙输出printpath(f.father)print(f.node)final=A_star(init)if final:print("有解，解为：")printpath(final)else:print("无解")