标题：Physics-Based Multi-Bias RF Large-Signal GaNHEMT Modeling and Parameter Extraction Flow (JEDS 17年)

模型描述

该模型的核心是对表面势（ψ）及其随施加的栅极电压（V_g）和漏极电压（V_d）变化的解析建模。在考虑了真实器件效应（如速度饱和、DIBL、迁移率退化、通道长度调制CLM，参见图1）之后，固有栅极电荷（Q_gi）和漏极电荷（Q_di）以及漏极电流（I_d）的表达式以公式$(1)$至$(3)$的形式书写。
$${\mathrm{Q}}_{\mathrm{gi}}=\mathrm{WL}{\mathrm{N}}_{\mathrm{f}}{\mathrm{C}}_{\mathrm{g}}\left\{{\mathrm{V}}_{\mathrm{go}}-\frac{({\psi }_{\mathrm{s}}+{\psi }_{\mathrm{d}})}{2}+\frac{{\psi }_{\mathrm{ds}}^2}{12({\mathrm{V}}_{\mathrm{go}}-\frac{({\psi }_{\mathrm{s}}+{\psi }_{\mathrm{d}})}{2}+\frac{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}{\mathrm{q}})}\right\}(1)$$
$${\mathrm{Q}}_{\mathrm{di}}=-\frac{\mathrm{WL}{\mathrm{N}}_{\mathrm{f}}{\mathrm{C}}_{\mathrm{g}}}{2}\left\{{\mathrm{V}}_{\mathrm{go}}-\frac{({\psi }_{\mathrm{s}}+2{\psi }_{\mathrm{d}})}{3}+\frac{{\psi }_{\mathrm{ds}}^2}{12\left({\mathrm{V}}_{\mathrm{go}}+\frac{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}{\mathrm{q}}-\frac{({\psi }_s+{\psi }_d)}{2}\right)}+\frac{{\psi }_{\mathrm{ds}}^3}{12}{\left({\mathrm{V}}_{\mathrm{go}}+\frac{{\mathrm{K}}_{\mathrm{B}}\mathrm{T}}{\mathrm{q}}-\frac{({\psi }_s+{\psi }_{\mathrm{d}})}{2}\right)}^{-2}\right\}(2)$$
$$I_{\mathrm{ds}}=\frac{{\mu }_{\mathrm{eff}}{C}_g}{\sqrt{1+{\theta }_{\mathrm{sat}}^2{\psi }_{\mathrm{ds}}^2}}\frac{W}{L}\left(V_{\mathrm{go}}-{\psi }_m+V_{\mathrm{th}}\right)\left({\psi }_{\mathrm{ds}}\right)\left(1+\lambda V_{\mathrm{ds}}\right)(3)$$
$${\psi }_m=({\psi }_d+{\psi }_s)/2$$

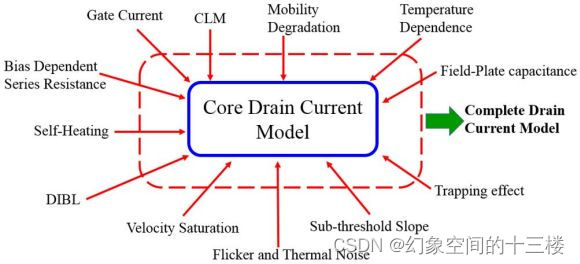
图 1. 为实现更接近实际器件行为的模型，在基于核心表面势垒的漏极电流模型中加入了多种非理想性因素。

为了捕捉GaN器件由于大面积接入区（AR）导致的开启电阻显著调制，特别是在漏极支持高击穿电压时，在核心模型基础上附加接入区电阻模型。接入区中的电流表示形式如（4）所示，其中L_acc为接入区长度，N_S0ACCS、V_SATACCS和U_0ACCS分别代表接入区二维电子气（2DEG）面载流子密度、载流子饱和速度和迁移率。
$${\mathrm{R}}_{\mathrm{ds},\mathrm{acc}}=\frac{{\mathrm{R}}_{\mathrm{c}}}{\mathrm{W}\cdot {\mathrm{N}}_{\mathrm{f}}}+\frac{{\mathrm{L}}_{\mathrm{acc}}}{\mathrm{W}\cdot {\mathrm{N}}_{\mathrm{f}}\cdot \mathrm{q}\cdot {\mathrm{N}}_{S0ACCS}\cdot {\mathrm{U}}_{0ACCS}}\times {\left(1-{\left(\frac{{\mathrm{I}}_{\mathrm{ds}}}{\mathrm{W}\cdot {\mathrm{N}}_{\mathrm{f}}\cdot {\mathrm{N}}_{S0ACCS}\cdot {\mathrm{V}}_{\mathrm{SATACCS}}}\right)}^2\right)}^{-1/2}(4)$$

直流参数提取

参数	描述
VOFF	截止电压
NFACTOR	子阈值斜率因子
CDSCD	SS退化因子
η0	DIBL参数
VDSCALE	DIBL参数
U0	低场迁移率
NS0ACCS	AR 2DEG密度
VSATACCS	AR饱和速度
RTH0	热阻

图 2.使用多偏压Id − Vg和Id − Vd曲线进行逐级直流参数提取流程。

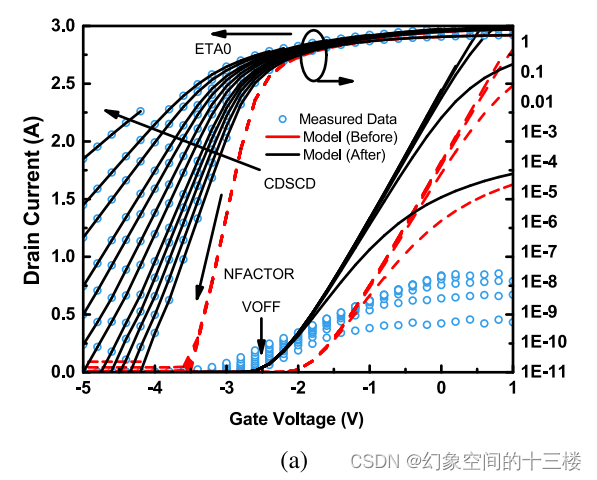
从Id − Vg线性数据中识别VOFF。在提取VOFF之后，从对数坐标Id − Vg曲线中优化NFACTOR、η0和CDSCD参数。

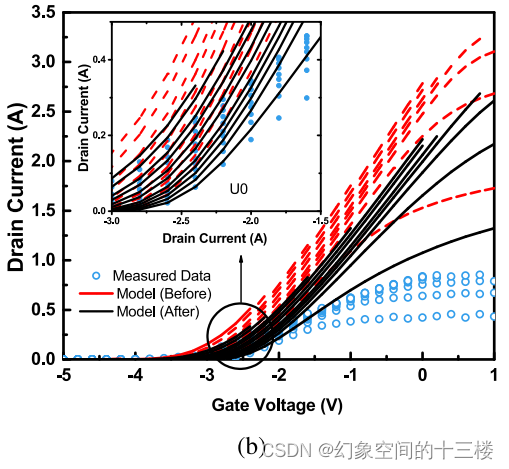
U0参数被优化以适应低栅极电压条件。

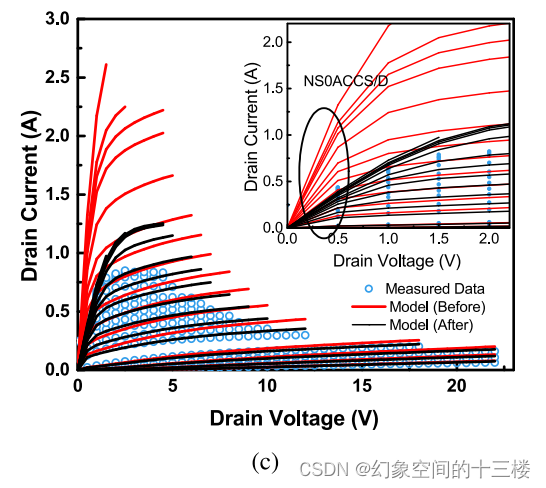
在Id与Vd曲线的线性区段中，通过调整NS0ACCS来拟合导通电阻。

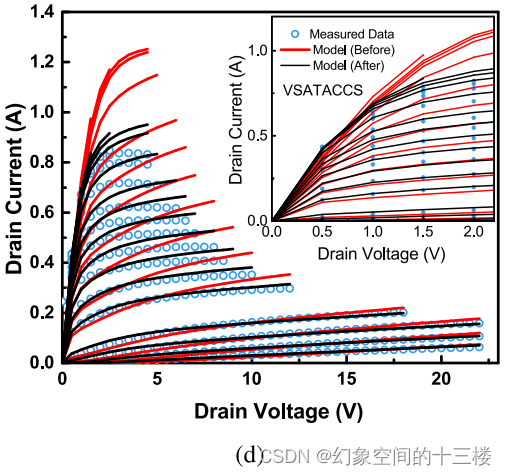
VSATACCS是通过拟合Id与Vd曲线中的饱和电流来提取的。

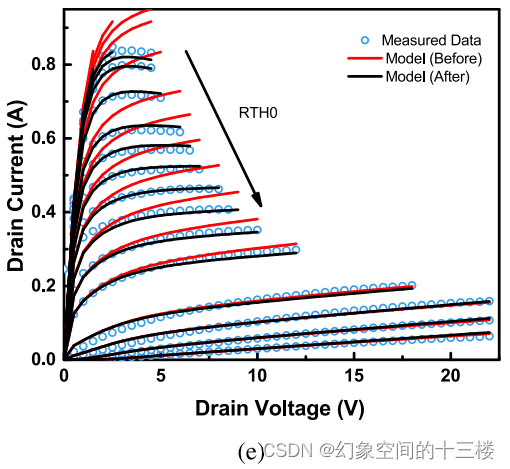
RTH0参数被调整以适应自热效应的拟合。模型在参数提取前后的结果分别用红色和黑色显示。

首先，图2(a)展示了在多个V_d条件下的I_d与V_g关系曲线，分别采用线性刻度和对数刻度。V_OFF可以从数据中识别出来，即当I_d开始上升时的V_g值，标志着亚阈值区间的结束。也可以通过广为人知的g_m-导数法或恒定电流法对其进行量化。所提取的VOFF值应与I_d − V_g对数坐标图相吻合，从而提供一个良好的初始V_OFF值，并可通过微调以实现更好的拟合。在同一幅图中，在亚阈值区域的对数坐标曲线上可以提取出N_FACTOR、C_DSCD、η₀和V_DSCALE等参数。其中，N_FACTOR是亚阈值斜率参数，可以通过优化来适应低V_d值下的亚阈值斜率。一旦确定了N_FACTOR，参数η₀就可以进行优化调整，以便随着V_d增加补偿DIBL（栅极电压引起的漏电流崩落）效应或V_OFF的退化。另外，η₀也可以通过对数据直接观察得到。对于相同的电流，在线性饱和V_d值之间的亚阈值曲线位移可大致估计η₀的大小；而V_DSCALE决定了V_OFF随V_d增加的变化速率。随着V_d增大，亚阈值斜率的恶化程度由C_DSCD决定。

低场迁移率参数U₀通过拟合I_d与V_g线性图中的低V_d和低V_g数据条件进行调整，这样可以合理地假设垂直电场以及沿沟道方向的电场导致的迁移率退化结果为U₀。图2(b)及其放大插图突出了优化U₀后得到的拟合结果。

AR参数N_S0ACCS和V_SATACCS分别从I_d与V_d的线性区和饱和区中提取，如图2©和2(d)所示。其中，N_S0ACCS对于决定导通电阻至关重要，而V_SATACCS则用于确定饱和电流水平。自热效应（SHE）采用标准的R-C网络方法建模，该方法包括一个热阻（R_TH0）和一个热容（C_TH0）。在热节点处电压的变化反映出温度的上升（ΔT），并将此温升值叠加到器件运行时的名义温度（T_NOM）上。DC-IV特性曲线中的高电流I_d与V_d区域呈现出负斜率，如图2(e)所示，这表明模型预测到了SHE效应，并且可以借此提取参数RTH0。上述描述的过程总结于图3中。

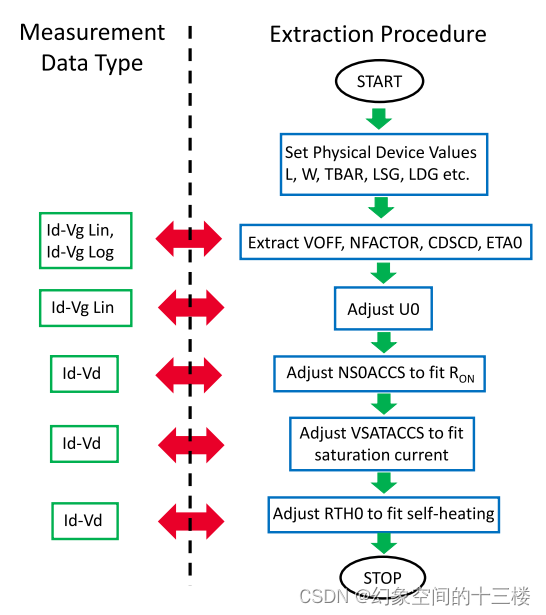
图3. 所述的直流参数提取流程，不仅用于拟合漏极电流，还用于获取器件的固有电容。AR模型如图2所示被整合进固有模型中。

陷阱效应的建模

为了准确估计GaN HEMT的大信号射频行为，建立精确的陷阱模型至关重要。与预期理论输出功率（V_ppI_pp/8）相比，射频功率放大器的实际输出功率下降现象可归因于各种陷阱效应的表现形式，例如电流崩塌、拐点漂移、漏极滞后、栅极滞后等。在图4所示的双脉冲模式下，采用1000 Hz脉冲频率和0.02%占空比进行脉冲IV特性表征，该测试在多种静态漏极和栅极偏压条件下进行，确保栅极电压和漏极电压同时从静态偏压点进行脉冲变化。脉冲宽度为200 ns，测量窗口在200 ns内的40 ns时段内足够短，以确保脉冲-IV特性的等温及动态同条件测量。

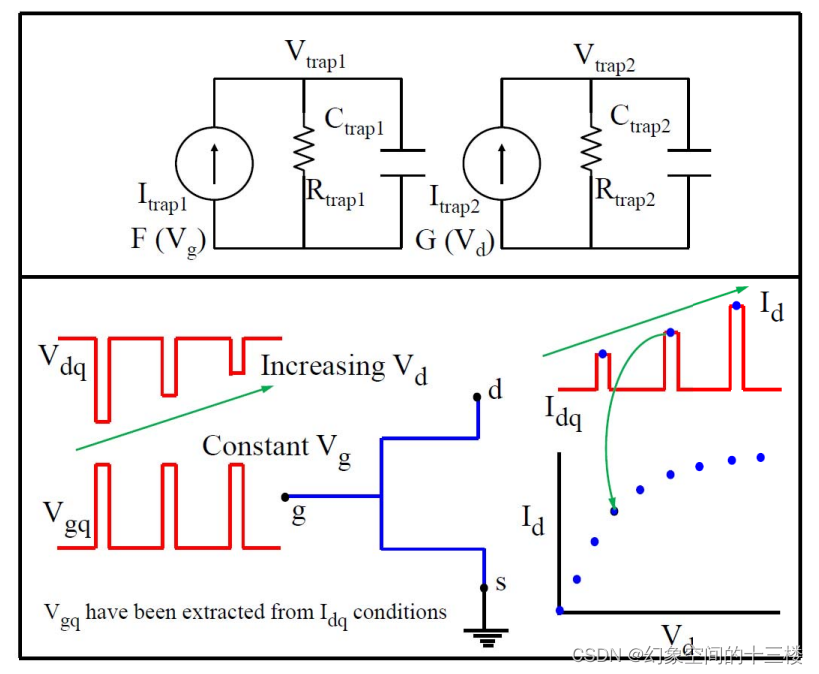
图4. (I) 用于模拟陷阱效应的两个R-C子电路，其中一个用于栅极滞后，另一个用于漏极滞后。电压V_trap1和V_trap2被反馈至紧凑模型中，以更新其关键参数，如(5)所示。 (II) 双脉冲方案进行脉冲-IV仿真。
$${\mathrm{V}}_{\mathrm{OFF}}(\mathrm{Trap})={\mathrm{V}}_{\mathrm{OFF}}+\left({\mathrm{V}}_{\mathrm{OFFTR}}\cdot {\mathrm{V}}_{trap2}\right)$$
$${\eta }_0(\text{Trap})={\eta }_0+\left({\eta }_{0\text{TR}}\cdot {\mathrm{V}}_{\text{trap}2}\right)$$
$${\mathrm{C}}_{\mathrm{DSCD}}(\mathrm{Trap})={\mathrm{C}}_{\mathrm{DSCD}}+\left({\mathrm{C}}_{\mathrm{DSCDTR}}\cdot {\mathrm{V}}_{\mathrm{trap}2}\right)$$
$${\mathrm{R}}_{\mathrm{ds}}(\mathrm{Trap})={\mathrm{R}}_{\mathrm{ds}}-\left({\mathrm{R}}_{TR1}\cdot {\mathrm{V}}_{trap1}\right)+\left({\mathrm{R}}_{TR2}\cdot {\mathrm{V}}_{trap2}\right)\text{\hspace{1em}(5)}$$
从图5中观察到，由于陷阱导致色散需要建模的四个最重要的参数分别是V_OFF、η₀、C_DSCD以及漏源极电荷储存电容电阻（R_ds）。采用如图4所示的两个R-C子电路对此进行建模。节点电压V_trap1和V_trap2分别代表栅极滞后和漏极滞后的影响，并将这两个电压反馈回模型中，用于更新V_OFF、η₀、C_DSCD和R_ds的值。其中，V_OFFTR、η_0TR、C_DSCDTR、R_TR1和R_TR2作为参数使用。如图5所示，在多种静态偏压条件下对脉冲I_d与V_g及I_d与V_d的精确模型拟合结果，验证了所提出的陷阱模型的有效性。


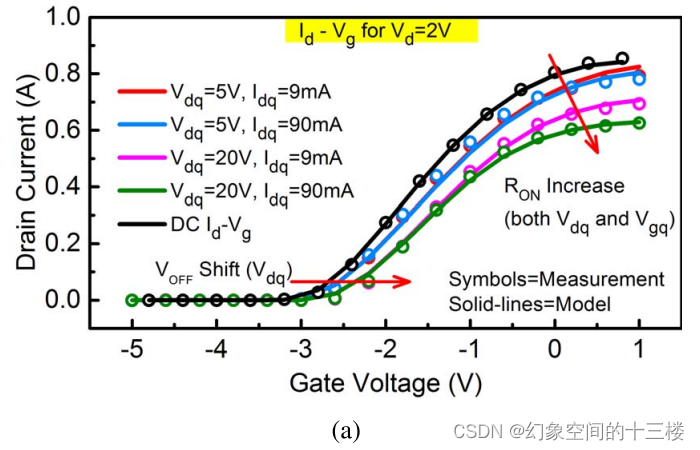
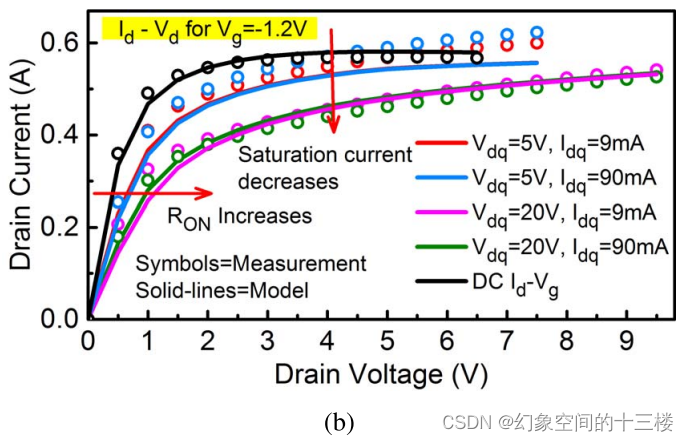
图5. 利用陷阱模型得到的测量值与模拟值之间关于(a)脉冲I_d-V_g特性和(b)脉冲I_d-V_d特性的相关性。在多种静态偏压条件（V_dq=5,20 V和I_dq=10,100 mA/mm）下观察到精确拟合结果，这对于模型非线性射频行为至关重要。

射频参数提取

图 6 中展示了射频小信号等效电路 (SS-EC)。整个 SS-EC 具有栅极 (GMF) 和漏极 (DMF) 区域或焊盘，分别将信号传递到栅极和漏极端口。它还有源极区域 (SMF) 或通孔，通过这些通孔，源极焊盘连接到背板金属化层。在这些区域之外，总线电感 L_xg、L_xd 和 L_xs 表示焊盘与实际 DUT 之间的连接，DUT 本身由工艺设计套件 (PDK) 控制。放大插图显示了 DUT 内部特征寄生电容 C_GS,p、C_GD,p 和 C_DS,p 以及访问电阻 R_g、R_d 和 R_s 的等效电路表示。

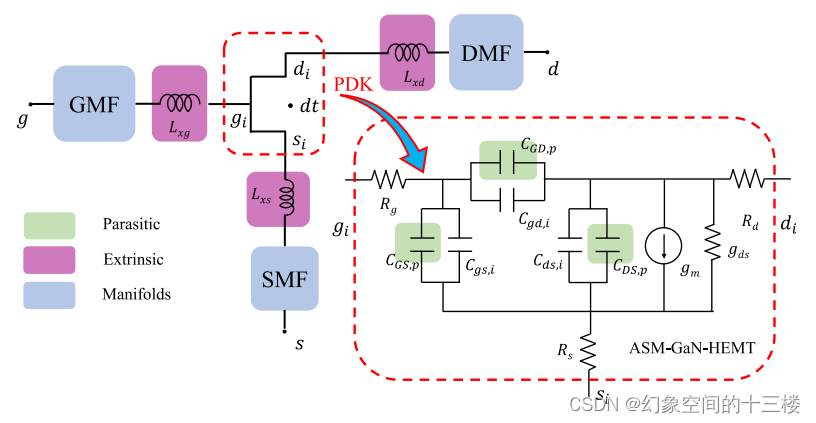
图 6. 包括由ASM-HEMT模型PDK描述的内在器件在内的整个设备的小信号等效电路模型。接入电阻Rg、Rd和Rs包含在内在核心模型中，而仅总线电感构成了外在级别的寄生参数。汇流条采用标准传输线模型进行模拟。

在完成直流-电压（DC-IV）参数提取的主要工作后，由于它们依赖于单一物理量ψ，因此同时确定了跨导（g_m）、输出电导（g_ds）、内在电容（C_gs,i、C_gd,i和C_ds,i）以及内在栅极电阻（R_g,i）。此外，在进行直流参数提取时，同时也对AR电阻（R_d和R_s）进行了拟合。所以，现在只剩下提取寄生电容以及栅极指状电阻（R_g,f）以及电感的任务。

Keysight的ADS模拟器进行所有模型仿真。在多种偏压条件下测量得到的宽频S-参数（0.5至50 GHz）被用于射频参数提取。通过采用晶圆上通反射载（Through Reflect Load, TRL）去嵌方法，对汇流条进行了去嵌，并得到了每个汇流条形式上的两端口S-参数文件。去嵌后的外在层测量结果自此被用于参数提取。

首先遵循标准低频Y参数法进行内在元件提取。需要注意的是，正如第三节中所述，在核心模型中包含了AR模型，因此我们可以利用这一优势，将R_s和R_d从内在的小信号等效电路(SS-EC)中省略掉，因为它们对跨导g_m和输出电导g_ds的影响已经通过AR模型得以体现。这样显著简化了在不牺牲准确度的情况下进行射频参数手工分析的过程，尽管省略了AR电阻，不会因遗漏这些电阻而影响准确性。

本征SS-EC元件测量值与模拟值的重叠图在频率轴上的对比结果如图7所示。通过调整寄生电容的数值以使电容曲线达到相应的水平，同时陷阱模型负责处理g_ds的色散现象。在模型中，g_m在低频段唯一表现出的色散是由自热效应引起的，并由自热参数R_TH0和C_TH0决定。不过，这些元素对偏压的依赖性已经由基于表面势核心模型妥善处理了。

在近10 GHz的频率范围内，这些元件对频率的准独立性表现良好，这是一个验证所提出射频模型有效性的标准基准。这意味着在出现感抗效应之前，我们拥有一个显著的提取范围。

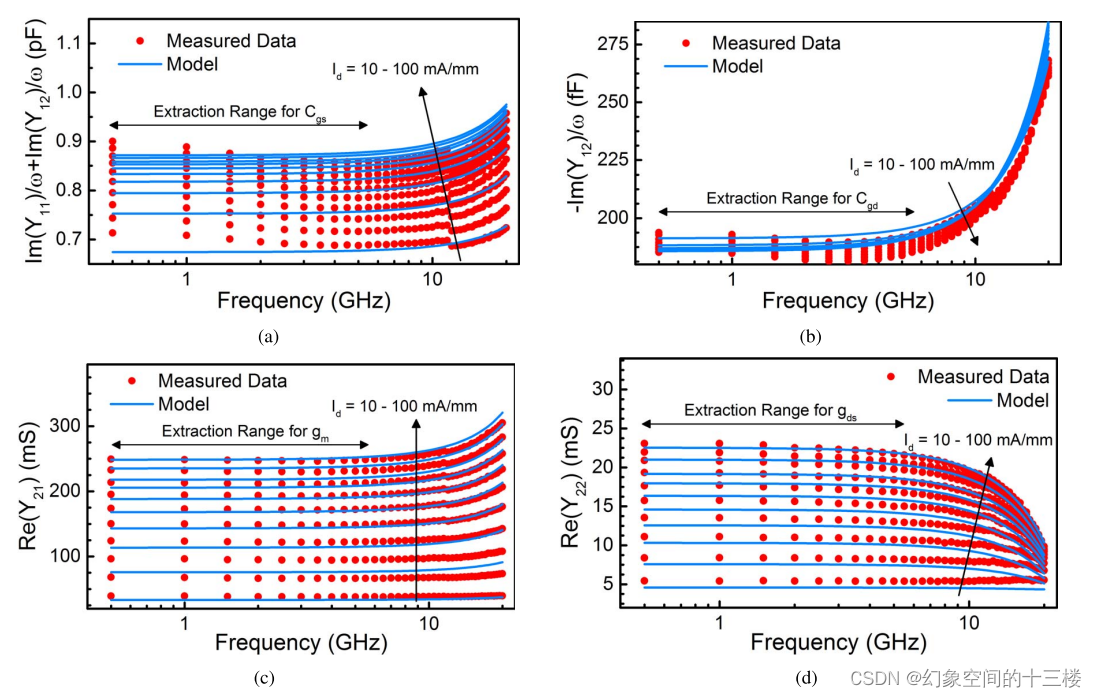
图7. 对于V_d = 5 V和10个栅极偏压条件提取得到的小信号等效电路(SS-EC)的 (a) C_gs、(b) C_gd、© g_m和(d) g_ds。为了使模型与测量数据拟合，已将寄生电容调整为表2中给出的数值以适应(a-b)部分的情况。观察到一个足够宽的频率范围（约10 GHz），在这个范围内SS-EC元件表现出频率无关的行为，在此之后感抗效应开始占主导地位。

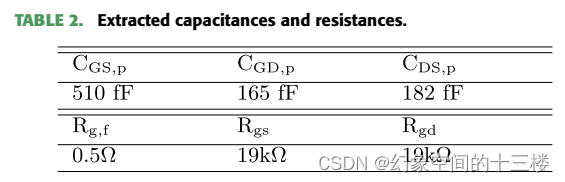
值得注意的是，当移动到更低的频率时，栅极电阻R_g会急剧增加（见图8(a)），这可归因于GaN器件中由于电流流过栅源和栅漏二极管而导致的栅极-通道微分电阻。通过在栅源和栅漏端子之间加入大电阻R_gs和R_gd来模拟这一现象，如图8(b)所示。尽管如此，仍能发现一个可观的频率范围用于提取栅指电阻R_g,f = R_g − R_g,i，这一点在图8(a)中得以展示。

表2中展示了提取出的寄生电容和电阻值。采用标准RC串联网络跨越漏极和源极节点来捕获基板损耗，如图8(b)所示。该衬底网络影响了在低频段观察到的g_ds色散现象，进而影响设备的S₂₂参数。理想情况下，对应RC衬底网络的时间常数应由低频Y参数确定。但由于设备宽带S参数测量数据从500 MHz开始，因此无法精确提取R_sub和C_sub的确切值。为此，选择了一个方便的时间常数，使其既能很好地解释500 MHz以下的g_ds色散现象，同时又能提供最佳拟合效果。在本研究中，将这个时间常数设置为50 μs或20 kHz。

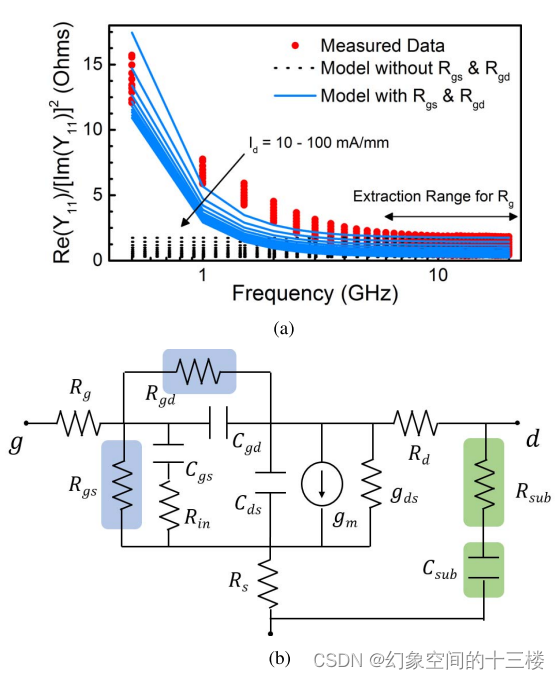
图 8. 为了捕获分别由栅源和栅漏肖特基二极管中电流导致的微分栅电阻，本征的小信号等效电路(SS-EC)中包含了大电阻R_gs和R_gd。它们的加入在低频时显著影响了整体栅电阻(R_g)，如图8(a)所示。R_sub和C_sub被包含进来以捕捉输出端口处的衬底损耗。需要注意的是，由于AR电阻R_s和R_d的影响已嵌入到g_m和g_ds中，因此在此省略不计。

值得注意的是，外在电感和偏压相关的本征电容会在更高频率产生共振现象，其具体表现为在外在层Y参数中出现的凹陷和峰值。如图9所示，这是一个示例说明。这些特征可以用于提取表3中列出的总线电感，以便匹配测量值与模型预测值对应的峰值。可以看出，由于电容随偏压变化而变化，该模型在捕获多种偏压条件下的共振行为方面具有高度准确性，从而作为验证模型提取过程的另一种方法。L_xs的负值可能归因于对衬底寄生效应的不适当校准或去嵌入处理。

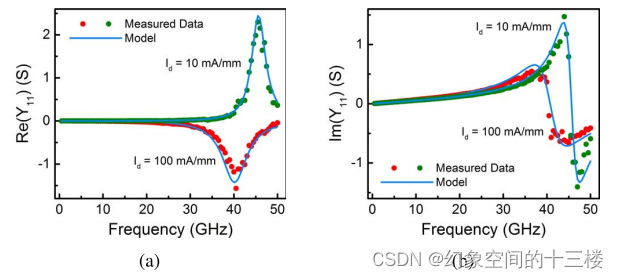
图 9. 展示了模型预测与测量得到的宽带外在层Y参数之间的比较。此处以Y₁₁为例进行说明。模型精确地捕捉到了峰值和谷值及其对偏压的依赖性，这反映了内在电容与外在电感之间相互作用的表现。可以通过微调总线电感的数值来匹配测量值与模型预测值在外在层Y参数中的峰值和谷值。

为总结射频参数提取过程，图10展示了频率范围在0.5至50 GHz之间的宽带S-参数重叠情况。结果显示了20种不同的偏压条件：漏极电压分别为5 V和20 V，并且栅极电压有10种不同的值，使得静态电流跨越了一个数量级（从10 mA/mm到100 mA/mm）。在各种不同偏压条件下，测量数据与模型之间呈现出高度相关性，这对于设计在不同漏极供电电压下的各类功率放大器(PA)来说是一项重要的模型能力。同时，该模型精确预测了S₂₂中拐点效应对偏压的依赖关系，这对于PA输出匹配网络的设计具有重要意义。整个参数提取流程直接明了，无需采用任何优化算法，如图11所示进行了总结概述。

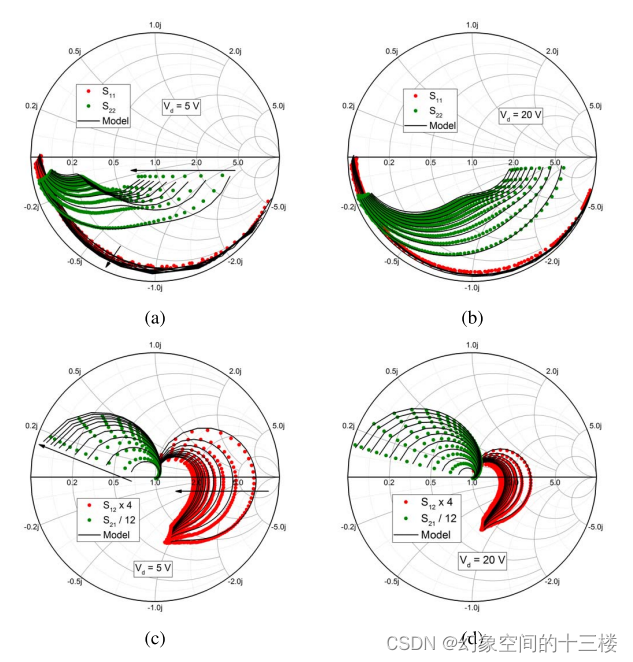
图 10. 对比了频率在0.5至50 GHz范围内的模型预测与实验测量得到的宽带外在层S-参数数据。Smith图展示了两种不同漏极偏压条件下的S₁₁和S₂₂（a-b）、S₁₂和S₂₁（c-d），每种漏极条件下有10种不同的栅极偏压（Id = 10至100 mA/mm）。该模型精确地捕捉到了S-参数对偏压的依赖性，这验证了核心内在模型以及射频参数提取过程的准确性。模型出色地再现了S₂₂中的拐点效应，突显了器件内在特性的卓越建模能力。箭头指示了电流I_d增加的方向。

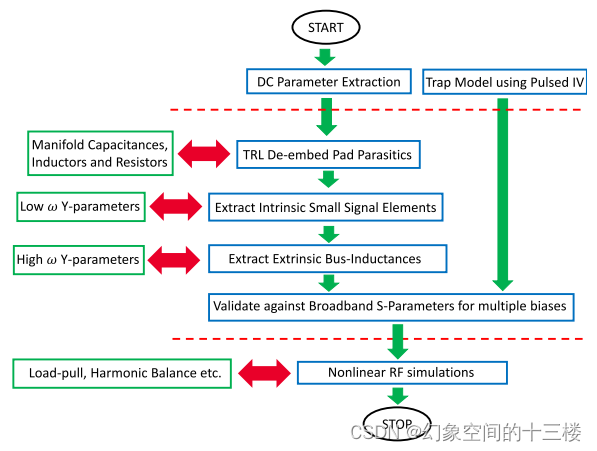
图11. 射频参数提取流程，用于提取GaN器件的射频小信号模型。该流程直接明了，无需进行任何优化，并通过如图10所示测量值与模拟宽带S-参数之间准确的相关性得到了验证。

大信号模型行为

为了检验所提出的模型的大信号性能表现，将测量数据与模型生成的输出功率（P_OUT）和功率附加效率（PAE）负载牵引曲线进行了对比分析。如图12(a)所示的是使用模型PDK和设备外在组件构建的ADS负载牵引原理图。通过Focus Microwaves提供的负载调谐器，在10 GHz基波频率下以输入功率（P_IN）为22 dBm获取了测量负载牵引数据。

为了更深入地理解负载阻抗对P_OUT和PAE的影响，在图12(b)至12(i)中将测量得到的负载牵引数据重新解释为离散负载扫描，并与模型估算结果进行了比较。结果显示，随着负载实部和虚部的变化，POUT和PAE及其相互之间的权衡关系均被模型精确捕捉到了。


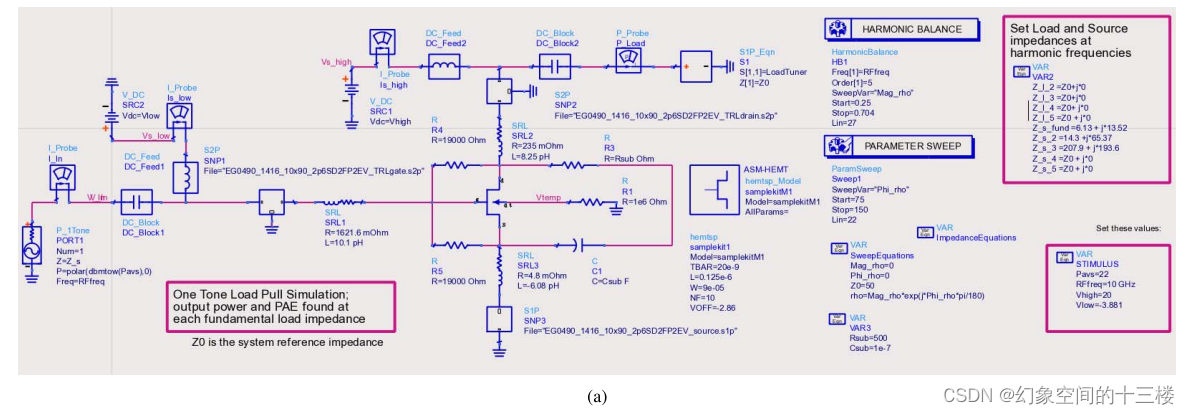
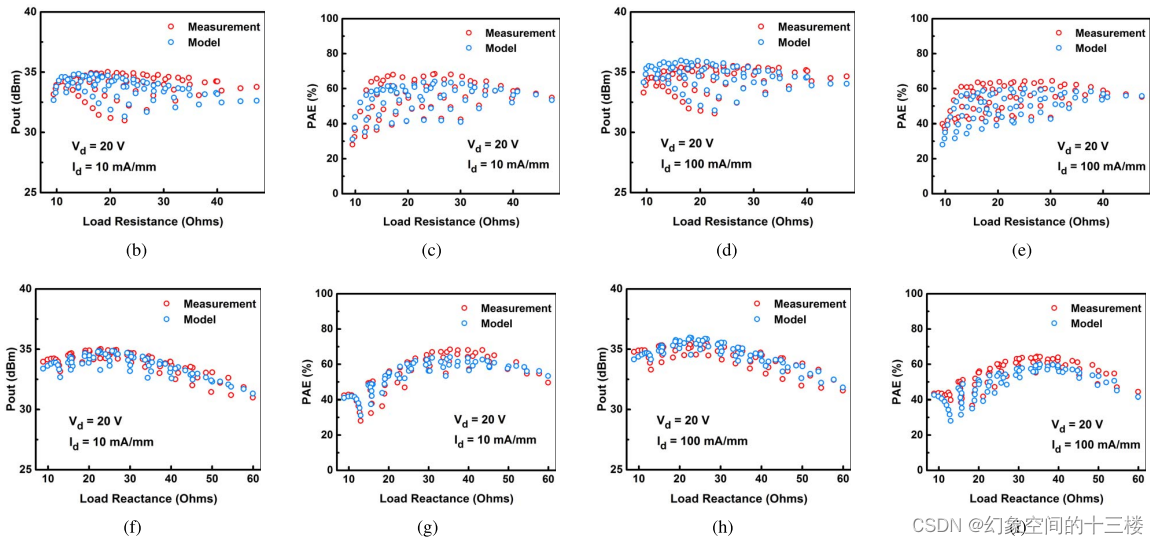
图 12. (a) 使用嵌入模型模拟负载牵引曲线的ADS原理图。以2端口S参数组件形式添加了焊盘级寄生效应。中央位置是受ASM-GaN-HEMT PDK控制的DUT（Device Under Test，待测器件）。
(b-i) 在10 GHz信号频率下，针对多种偏置条件，分别展示了P_OUT和PAE随着实部负载电阻和虚部负载电抗变化的离散负载扫描结果。该模型准确预测了P_OUT和PAE的最大值及其在改变负载阻抗时相互之间的权衡关系。

表4中给出了在不同栅极偏压条件下，通过负载牵引曲线获得的实现最大P_OUT和PAE的最佳负载阻抗值。在图13(a)至13(d)中，测量数据与模拟轮廓的重叠显示了高度相似性，这突显了所提出模型能够准确捕捉GaN HEMT非线性特性的能力，从而有效地预测POUT和PAE。由于负载牵引数据是在焊盘级进行测量的，因此在ADS模拟器中构建模型时，需要将提取的汇流条结构添加到外在层模型中，如图12(a)所示。

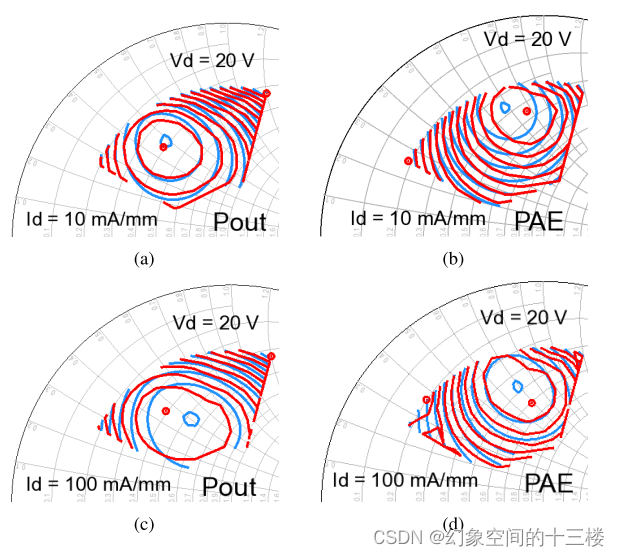
图13. 对比了在V_d = 20 V时，两种电流密度I_d分别为10 mA/mm和100 mA/mm条件下测量的和模拟得到的P_OUT（a, c）与PAE（b, d）负载牵引曲线。在标准50欧姆阻抗下，史密斯圆图区域对幅度范围0.26 < Magnitude($\Gamma$) < 0.71和相位范围70° < Phase($\Gamma$) < 160°进行了采样。该模型准确预测了随着负载阻抗变化时，POUT和PAE的最大值及其相互权衡关系。红色轮廓：实测数据；蓝色轮廓：模拟数据。

最后，进行了功率扫描仿真研究，以考察当器件进入压缩区域时模型的性能表现，如图14所示。负载阻抗设置为最大PAE状态。该模型在预测器件非线性行为方面表现出色，特别是在器件达到非线性区域后增益压缩现象以及随后在功率回退时PAE峰值的表现。通过精确模拟大信号工作条件下陷阱效应和自热现象，该模型能够在多种偏置条件下实现这样的准确性。这些结果表明，该模型已经准备好作为基于GaN HEMT技术的先进射频电路设计行业标准使用。

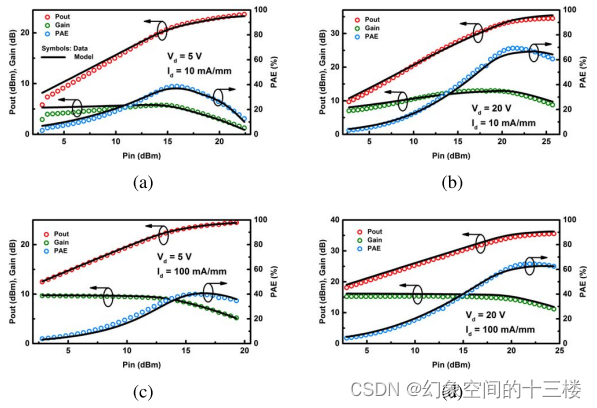
图14. 比较了模型模拟与实测的P_OUT（输出功率）、增益和PAE（功率附加效率）作为可用输入功率（PIN）函数的变化情况，其中V_d分别设置为5 V和20 V，并考虑两种栅极偏压条件I_d = 10 mA/mm和100 mA/mm。22 dBm射频输入信号的工作频率为10 GHz，负载阻抗值设定为实现最大PAE。模型精确地再现了增益压缩现象，这表明该模型准确地捕捉到了非线性特性。

结论

本研究展示并成功验证了一种基于表面势的GaN HEMT射频大信号模型，该模型针对商业GaN器件的测量数据进行了验证。研究发现，通过拟合模型以匹配直流-电压（DC-IV）特性曲线，由于器件本征电荷与电流之间的自洽性，将自动生成用于射频模拟的小信号等效电路，除了寄生电容和栅极电阻需要采用标准程序进行提取之外。此外，还利用RC电路对陷阱效应进行了建模，并使用宽带S参数对射频模型进行了验证。进一步地，该模型展示了其预测不同负载阻抗下负载牵引曲线及其对应最大值的能力，这对于精确进行功率放大器的一次性设计十分有用。