目录
一. 介绍
二. 完美安全的密钥与消息空间
三. 完美安全的密钥长度
四. 最优的完美安全方案
五. 香农定理
(1)理论分析
(2)严格的正向证明
(3)严格的反向证明
六. 小结
一. 介绍
一次一密方案,英语写做one time pad encryption scheme
一次一密方案可以实现完美安全(perfectly secret),但是这些方案是有局限性的,比如所有完美安全的方案密钥空间都要大于等于消息空间,这个定理待会我们会利用密码学专业术语进行证明。
如果假定密钥的长度固定,消息空间(message space)里的明文长度也固定的话,那么完美安全就要求密钥的长度大于等于消息的长度。当然,如果密钥和消息长度一样的话,就像一次一密那样,则是最优的情况。
除了这一个限制外,完美安全还要求密钥只能使用一次,具体证明则留给读者了。
二. 完美安全的密钥与消息空间
一个密码方案可以抽象成如下三个算法:
Gen,Enc,Dec
如果说该密码方案是完美安全的,他的消息空间为M,密钥空间为K,那么一定可得:
证明:
此处我们利用反证法。也就是证明,如果|K|<|M|,那么该方案一定不是完美安全的。
首先假定|K|<|M|。
不妨假设明文在M上是均匀分布的。从密文空间C中选择一个密文c,并且该密文的概率不为0,也就是:
对于该密文c来讲,使用不同的密钥k可能会得到不同的明文。我们将所有的可能性形成一个集合称之为M(c),如下:
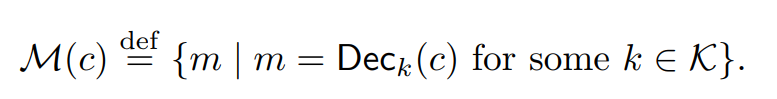
并不是每个密钥解密都有效,所以很容易可得该集合的空间小于等于密钥的空间,注意包含等于号就是恰好每个密钥都有效,那么可得:
大家可以把该过程的解密算法看成是确定性算法(deterministic)。
根据我们的条件假设,密钥空间小于明文空间,也就是|K|<|M|,那么必然存在一部分的明文不在该集合中,也就是:
所以可得:
![]()
该概率代表已知密文c,不可能会解密得到m',因为你已经尝试了所有的密钥。
但是m'在明文空间中是有概率的,也就可以得到:
![]()
从敌手的角度来讲,这就是泄露的信息。在已知密文情况下,明文的信息被泄露了一部分。所以很明显该方案不是完美安全的。
三. 完美安全的密钥长度
以上讨论告诉我们,完美安全不能无限降低密钥的长度,也可以将其看成完美安全的局限性。当然,现如今总是会出现一些非密码学的文章解释说设计出了一个新的加密方案,方案是无法攻破的,并且实现了类似一次一密的安全性,而且密钥的长度还小于明文的长度。很明显这类说法要么就是非严格密码学的局外人,要么就是方案本身是错的。
四. 最优的完美安全方案
在香农(Shannon)对完美安全的解释工作中,他指出密钥生成算法Gen要从所有可能的密钥中均匀输出密钥,就像一次一密方案。对于任意的明文m和密文c,都会存在唯一的密钥来匹配m和c,这个和一次一密方案也很类似。
这些有用的特征都可以用来证明方案的完美安全。换句话说,明文,密文和密钥的尺寸都是相等的,也就是:
|M|=|K|=|C|
在之前的证明中,我们已经严格证明完美安全要求:
借助映射定理,要想解密算法不出错,则要保证密文空间要大于等于明文空间,也就是:
通过以上的这些讨论我们不难得出,最优的完美安全方案需要保证:
|M|=|K|=|C|
五. 香农定理
将加密方案表示成:
(Gen,Enc,Dec)
其中消息空间为M,且满足:
|M|=|K|=|C|
那么如果方案满足如下两个条件,则可以说明他是完美安全的:
(1)Gen从密钥空间中输出密钥k,如下:
其对应的概率均相等,都为1/|K|
(2)任意选择明文m和密文c,也就是:
都能从密钥空间K中找到对应的密钥k,也就是:
使其满足:
需要将此处的Enc看成加密算法。
完整形式化的定理如下:

证明该定理:
遵循充分必要条件,该定理需要正向证明和反向证明。
(1)理论分析
首先需要根据给定的两个条件,来证明完美安全。首先观察条件2,因为总存在密钥k将对应的明文m和密文c对应,所以密文c和明文m可能存在任意的对应关系。又因为密钥是唯一存在的,且每个密钥的概率均相等,正如一次一密方案,完美安全则很容易被证明。
接着需要根据完美安全,来解释这两个条件成立。完美安全意味着,对任意的明文m和c都至少存在一个密钥使得他们互相对应,再根据:
|M|=|K|=|C|
可以证明对应的密钥只有唯一性存在,那么就很容易说明每个密钥被选取的概率都是相等的,否则完美安全则不成立。
(2)严格的正向证明
不失一般性,可假设加密算法Enc是确定性的。我们首先需要根据条件1和条件2来证明该密码方案是完美安全的。这个证明过程在此专栏的前面有介绍过。
从密文空间C中选取一个密文c,从明文空间M中选取一个明文m,也就是:
令k代表某唯一的密钥,且满足:
![]()
进一步可计算得到:

第一个等号:对应成功的关键在于密钥选择正确
第二个等号:条件1表明
此等式对任意的m和c都是成立的,那么可以直接得出该方案是完美安全的。
(3)严格的反向证明
现在我们已知是完美安全,需要证明条件1和2成立。
选取任意密文:
一定会存在对应的明文m*满足:
![]()
这也就意味着对任意的明文:
其概率均不为0,也就是:
![]()
那么进一步我们将明文写成集合的形式:
![]()
进一步可得:
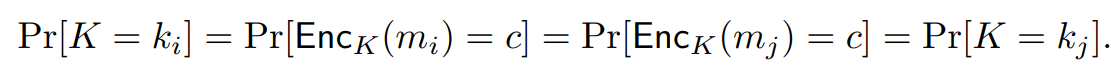
接着很容易证明可得。
六. 小结
在网络安全领域,香农定理可用于证明给定的方案是否为完美安全。






java#Springboot#mysql旅游景点订票系统68524-计算机毕业设计项目选题推荐)




VFS 与编辑器)


——条件生成对抗网络(Conditional Generative Adversarial Network, CGAN))
)
:多代理协作(Multi-Agent Collaboration))
挂载?)

