基本思想：

利用多层次蒙特卡洛方法（Multi-Level Monte Carlo，MLMC）和Actor-Critic算法，解决平均奖励强化学习中的快速混合问题。

快速混合？

在强化学习中，当我们说一个策略"混合得快"，是指该策略在探索和利用之间达到一个良好的平衡，从而使学习过程更快、更有效。

提出的背景：

现有的强化学习方法在后端使用的是stochastic gradient descent（随机梯度下降），基于数据生成过程与步长选择中出现的速率参数以指数速度混合的假设，但对于较大状态空间或具有稀疏奖励的情况，这个假设并不成立。因此提出MAC这一个方法，是将蒙特卡洛利用于critic网络，actor网络和AC算法中的平均奖励，既不依赖于参数选择中混合时间的预测知识，也不假定其指数衰减。

随机梯度下降 (Stochastic Gradient Descent，SGD) 是一种选代优化算法，用于最小化代价函数J(theta)。该算法在每次迭代时随机选择一个训练样本，并利用该样本对模型参数theta进行更新然后重复这个过程多次。

混合速率？

如果环境是高度随机性的或存在很多障碍，这时智能体可能会长期停留在固定的一个状态下，到达稳态的总变化的变化距离是在缓慢减小的，也就是mixing rate，混合速率较慢。

许多强化学习的环境由于高纬度、内在波动性、稀疏奖励或包含不同的子任务导致它们表现出比指数级环境更慢的混合速率。

论文中关于mixing time的定义是：

主要思路：

将多层次蒙特卡洛方法与Actor-Critic算法相结合，通过同时更新策略和状态-行为值函数来寻找最优策略。在多层次蒙特卡洛方法中，Actor部分使用低层次的蒙特卡洛模拟来快速更新策略，而Critic部分使用高层次的蒙特卡洛模拟来精确计算状态-行为值函数的更新。

MAC算法的伪代码：

与传统AC算法不同的是，中间利用了MLMC算法，即多层次蒙特卡洛方法，对参数进行更新。

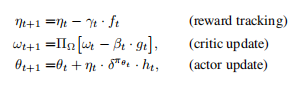
论文作者是在Dorman&Levy所研究出的MLMC和AdaGrad步长选择器基础上开发出一个MLMC梯度估计器。

Adagrad优化算法被称为自适应学习率优化算法，之前我们讲的随机梯度下降对所有的参数都使用的固定的学习率进行参数更新，但是不同的参数梯度可能不一样，所以需要不同的学习率才能比较好的进行训练，但Adagrad 的核心想法就是，如果一个参数的梯度一直都非常大，那么其对应的学习率就变小一点，防止震荡，而一个参数的梯度一直都非常小，那么这个参数的学习率就变大一点，使得其能够更快地更新。

论文实验：

算法环境是一个NxN网格，起始位置在左上角，目标位置在右下角。智能体有五个动作：停留、上、下、左和右，到达目标位置给予+1奖励，其余位置为0奖励。