AcWing 2. 01背包问题（DP思想）

[题目概述]

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 $v_i$ ，价值是 $w_i$ 。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。
接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

$0 < N, V \leq 1000$
$0<v_i,w_i≤1000$

输入样例

输出样例：

分析问题
题目让我们从n件物品中选若干件物品，且总体积不超过v，并从所有方案中找出总价值最大的。
题目设计求最大最小值和数量就可能是用动态规划的思想来求解了。
- 思路解读
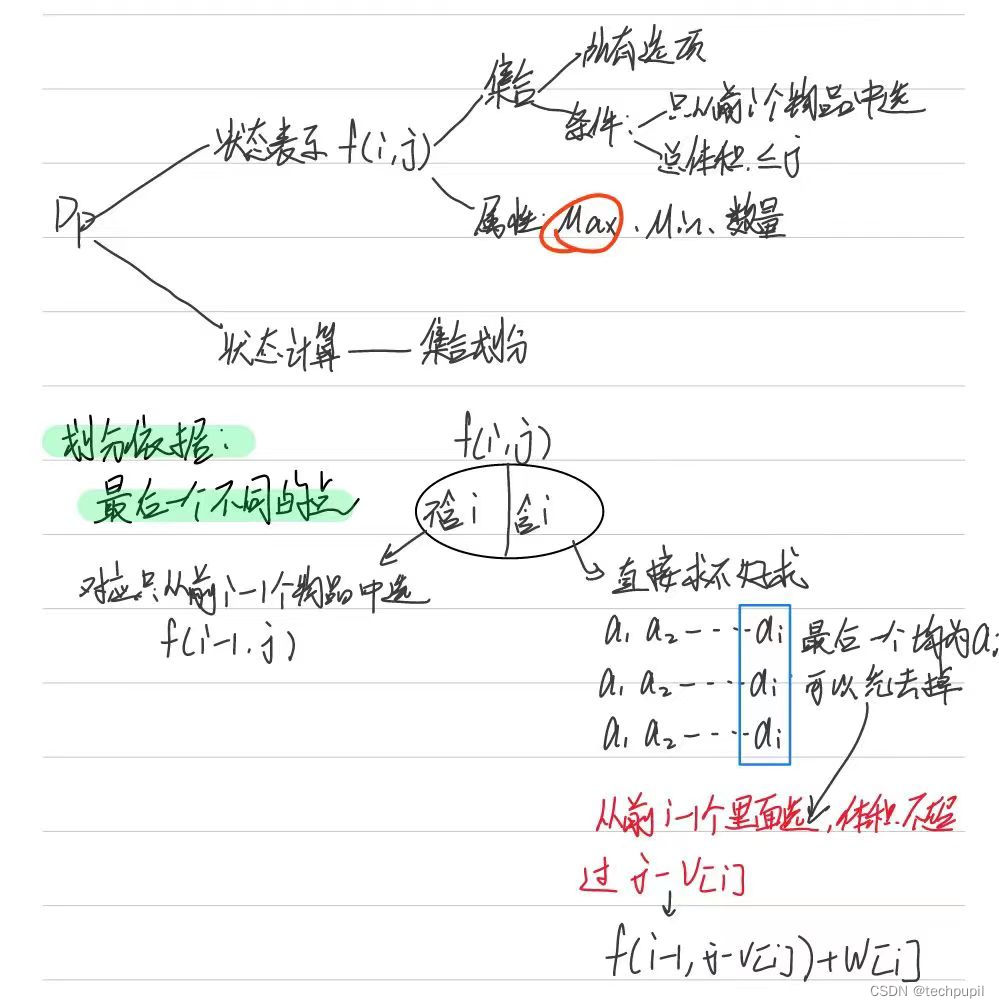
首先动态规划问题可以分为状态表示和状态计算来思考。其中状态表示有可分为集合和属性，本题中 f(i, j) 表示的是从前 i 个物品中选择体积不超过 j 的方案，属性就是最大值，那么状态表示用一句话就是从前 i 个物品中选择体积不超过 j 的物品总价值的最大值。
其次，状态计算就是集合划分，将 f(i, j) 划分为几个我们能求出的块，本题可以分成两个部分，选的物品中是否包含 i , 那么左边不含 i 就可以看做是从前 i - 1个物品中选择总体积不超过 j 的方案，所以左边就是 f(i , j) 。
右边可能为空，加入第 v[i] > j 那么右边一定是不成立的。v[i] <= j 的话，如果直接求的话，很难求，此时我们可以曲线救国一下，既然右边的所有方案中都含第 i 个数，我们可以把他单独提出来，那右边是不是就可以等价于 f(i - 1, j - v[i]) + w[i] ,这样我们就可以很轻松的求出来。
完整代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;const int N = 1005;
int n, m;
int v[N], w[N];
int f[N][N];
int main () {cin >> n >> m;for (int i = 1; i <= n; i ++)cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++) {for (int j = 1; j <= m; j ++) {f[i][j] = f[i - 1][j];if (v[i] <= j)f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);}}cout << f[n][m];return 0;
}

优化版本
DP的优化就是针对代码的优化，而不针对题，就是看在代码改变后是否和原来求的是一个意思。
就是将二维变一维，直接将第一层删掉

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;const int N = 1005;
int n, m;
int v[N], w[N];
int f[N];
int main () {cin >> n >> m;for (int i = 1; i <= n; i ++)cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++) {for (int j = 1; j <= m; j ++) {// 变成了恒等式，可以删除f[j] = f[j];if (v[i] <= j)// 现在关键就是看这行和原来是不是一个东西，答案是否// 它现在等价于 f[i][j] = max(f[i - 1][j], f[i][j - v[i] + w[i])// 因为我们 j 现在是从下到大进行枚举，而j - v[i]是比 j 小的，而i是固定的，// 所以他在 i - 1层的时候就已经求出来了,所以我们只要将 j 从大到小进行枚举即可f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[n][m];return 0;
}

优化后的最终代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;const int N = 1005;
int n, m;
int v[N], w[N];
int f[N];
int main () {cin >> n >> m;for (int i = 1; i <= n; i ++)cin >> v[i] >> w[i];for (int i = 1; i <= n; i ++) {// j 大于v[i] 才有此情况for (int j = m; j >= v[i]; j --) {f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m];return 0;
}