排序（插入排序）

现在，我们学习了之前数据结构的部分内容，即将进入一个重要的领域：排序，这是一个看起来简单，但是想要理清其中逻辑并不简单的内容，让我们一起加油把！

排序的概念及其运用

排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

排序运用

商品排序
院校排名
除了这些还有其他的一些地方也会用到排序，总之，我们的生活中处处都存在着排序，所以，学习好排序的使用，对于我们后续学习是十分重要的

常见排序算法

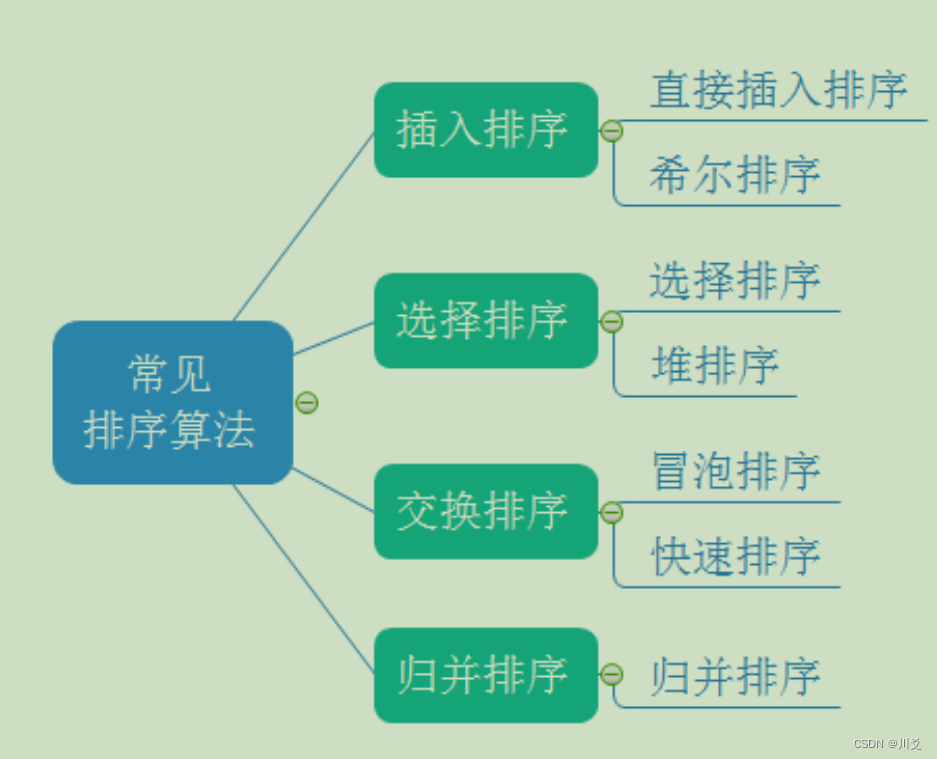
在这里插入图片描述
而我们今天讲的重点就是插入排序：其中包含着的就是直接插入排序和希尔排序，而希尔排序事实上就是直接插入排序的升级版

插入排序

基本思想：
直接插入排序是一种简单的插入排序法，其基本思想是：
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。

直接插入排序

当插入第i(i>=1)个元素时，前面的array[0],array[1],…,array[i-1]已经排好序，此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较，找到插入位置即将array[i]插入，原来位置上的元素顺序后移
直接插入排序的特性总结：

元素集合越接近有序，直接插入排序算法的时间效率越高
时间复杂度：O(N^2)
空间复杂度：O(1)，它是一种稳定的排序算法
稳定性：稳定

我们首先给一个例子为大家讲解一下其中的原理：

int a[ ]={6 9 1 2 5};
假设此时我们要排序的是1，那么我们用end+1作为插入排序元素的下标，end则是前面已经排好顺序的一段，范围为[0,end]。此时我们用一个变量记录住1的值，然后往前比对。我们发现，1比9小，所以end+1下标的位置变为9，然后end–；1比6小，6又被赋值到了原本9的位置上；最后再把1赋值到下标0的位置上，一次排序就成功了。
写成代码是这个样子的：

int end;
int tmp=a[end+1];
while(end>=0){if(tmp<a[end]){a[end+1]=a[end];end--;}else{break;}
}a[end+1]=tmp;

为什么while循环的结束条件是end>=0呢，拿上面的举例，一开始end+1的下标为2，也就是end为1，end- -之后变成了0，而第二次end- -之后直接变成了-1，退出循环。此时end+1=0，也就是数组的第一个元素，最小的元素，刚好就是1

但很明显，这样的话这个函数只能比较一次，怎么样才可以实现多次比较呢，这个时候就需要在外面嵌套一个for循环，然后从0开始一个一个比对，直到n-2（如果是n-1，end+1就是n，就超过数组的下标了，会越界）
所以最终的直接插入排序是这样写的：

//插入排序：前一段有序，在后方插入一个并再次排序
//[0,end] end+1大概就这个意思
//时间复杂度：O(N^2)
//最好的情况：O(N)，就算有序也得遍历一遍
void InsertSort(int* a,int n) {for (int i = 0; i < n - 1; i++) {int end = i;int tmp = a[end + 1];while (end >= 0) {if (tmp < a[end]) {a[end + 1] = a[end];end--;}else {break;//终止循环}}a[end + 1] = tmp;}
}

希尔排序（缩小增量排序）

希尔排序（Shell’s Sort）是插入排序的一种更高效的改进版本，也称为缩小增量排序。它的基本思想是：先将整个待排序的记录序列分割成为若干子序列（由相隔某个“增量”的记录组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

希尔排序的增量序列的选择是一个数学难题，通常选取这个常用的增量序列：t1=n/2，ti=ti-1/2，直到ti=1为止。其中，n为待排序序列的长度。按照增量序列的个数k，对序列进行k趟排序。每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。

只看概念会觉得晦涩难懂，还是先给大家举一个例子看看：
在这里插入图片描述
假设有这么一个数组，我们要对其进行希尔排序，通常会分成两个步骤：
1.预排序：首先将其分为几个组，然后针对每个分组进行插入排序
2.预排序之后，此时数据已经趋于有序，我们再对其整体进行直接插入排序

在这里的话，我们假设间隔3个为一组，那么9，6，3，0就是一组，8，5，2是一组，7，4，1是一组，而我们对每个组进行插入排序之后，顺序就分别变成：0，3，6，9；2，5，8；1，4，7；而放在整体中的话，就是0 2 1 3 5 4 6 8 7 9，可以看出，次序比起一开始的逆序已经好了很多，如果将这一次排序写成代码，就是这个样子的：

	int gap=3;//j<n-gap是因为防止越界//内层的for循环只可以提供一组的排序，而外部for循环使每一个组都排序//i=0,i=1,i=2，三个组都可以排序for(int i=0;i<gap;i++){for(int j=i;j<n-gap;j+=gap){int end=j;int tmp=a[end+gap];while(end>=0){if(tmp<a[end]){a[end+gap]=a[end];end-=gap;}else{break;}} a[end+gap]=tmp;}}

但是很明显，这样子的话，只比较排序了一次，但我们需要的是在保证最后一次比较是gap==1的情况下，前面的预排序也要到位。但首先我们先把预排序的函数再修改一下，让它不用分组排序，而是多组并排。

int gap=3;
for(int i=0;i<n-gap;i++){int end=i;int tmp=a[end+gap];while(end>=0){if(tmp<a[end]){a[end+gap]=a[end];end-=gap;}else{break;}}a[end+gap]=tmp;
}

这样子的话，就不是一个一个组的排，而是从第一个元素开始，按照其组别来排顺序，相对于分组比较，多组并排明显更简洁

完成这些之后，我们就可以着手开始实现真正的希尔排序了！

void ShellSort(int* a,int n){int gap=n;//gap>1时是预排序，目的：接近有序//gap==1时就是直接插入排序，目的：有序while(gap>1){gap=gap/2;//让其预排序之后最终gap==1，进行最终的直接插入排序//gap越大，大的值更快调到后面，小的值可以更快的调到前面，越不接近有序；gap越小，跳得越慢，但是越接近有序。//gap=gap/3+1;也可以，效率更高，时间复杂度更低，一个是log2N，一个是log3Nfor(int i=0;i<n-gap;i++){int end=i;int tmp=a[end+gap];while(end>=0){if(tmp<a[end]){a[end+tmp]=a[end];end-=gap;}else{break;}}a[end+gap]=tmp;}}

那么大家一定很好奇，这么复杂的希尔排序，它的时间复杂度相较直接插入排序相比是否有进步，它的使用效率是否高于直接插入排序，接下来我就为大家来展示一下它们的差别。

int main() {int size = 10000;int arr[10000];// 使用时间种子初始化伪随机数生成器srand(time(0));// 填充数组for (int i = 0; i < size; i++) {arr[i] = rand() % 1000;  // 生成0到999之间的随机数}clock_t start, end;double cpu_time_used;// 测试插入排序的执行时间start = clock();InsertSort(arr, size);end = clock();cpu_time_used = ((double)(end - start)) / CLOCKS_PER_SEC;printf("InsertSort took %f seconds to execute \n", cpu_time_used);// 测试希尔排序的执行时间start = clock();ShellSort(arr, size);end = clock();cpu_time_used = ((double)(end - start)) / CLOCKS_PER_SEC;printf("ShellSort took %f seconds to execute \n", cpu_time_used);return 0;
}

在这里插入图片描述
可以看出，在初始化10000个随机数的数组中，直接插入排序和希尔排序之间的效率差了几十倍，而如果数据更多，可能差的还会更多。

在最坏情况下(完全逆序），希尔排序的时间复杂度是O(n^2)，这与直接插入排序的时间复杂度相同，但是在一般情况下其平均时间复杂度要优于O(n ^2)。希尔排序时间复杂度的优劣程度取决于间隔序列的选取，不同的间隔序列的希尔排序的时间复杂度也会有所不同。

在实际使用中，通常使用增量序列为n/2,k=k/2,…1的希尔排序，在平均情况下，其时间复杂度大约介于O(n^1.3)和O(n ^2)之间，这使得希尔排序在中等规模数据时具有较好的性能。

其实我们自己也可以简单分析一下，以最坏情况来看：
gap很大时，gap==n/3+1，此时我们忽略+1 。这一趟每组3个，移动次数：第二个最多移动1次，第三个最多移动2次，合计为3；而总计有3/n组，累计移动的次数是（1+2) * 3/n=n
而下一轮预排序，gap==n/9，每组9个，移动次数：1+2+3…+8=36；总计n/9组，累计移动次数4n，但这是最坏的情况下做出的判断，在经历过第一次排序之后，已经比刚才更接近有序，不会所有的元素都要排序，所以次数必定是小于4n的，而后面的预排序也是与这个一样的，所以我们并不确定其时间复杂度，只能算出一个大概的区间，具体情况只能跟当前排序的数据元素相关，需要经过大量分析才能得出结论。

以上就是排序的第一讲：插入排序！下一节我们将会讲解选择排序，欢迎大家关注后续文章！