题目

幼儿园里有 N 个小朋友，老师现在想要给这些小朋友们分配糖果，要求每个小朋友都要分到糖果。

但是小朋友们也有嫉妒心，总是会提出一些要求，比如小明不希望小红分到的糖果比他的多，于是在分配糖果的时候， 老师需要满足小朋友们的 K 个要求。

幼儿园的糖果总是有限的，老师想知道他至少需要准备多少个糖果，才能使得每个小朋友都能够分到糖果，并且满足小朋友们所有的要求。

输入格式

输入的第一行是两个整数 N,K。

接下来 K 行，表示分配糖果时需要满足的关系，每行 3 个数字 X,A,B。

• 如果 X=1．表示第 A 个小朋友分到的糖果必须和第 B 个小朋友分到的糖果一样多。
• 如果 X=2，表示第 A 个小朋友分到的糖果必须少于第 B 个小朋友分到的糖果。
• 如果 X=3，表示第 A 个小朋友分到的糖果必须不少于第 B 个小朋友分到的糖果。
• 如果 X=4，表示第 A 个小朋友分到的糖果必须多于第 B 个小朋友分到的糖果。
• 如果 X=5，表示第 A 个小朋友分到的糖果必须不多于第 B 个小朋友分到的糖果。

小朋友编号从 1 到 N。

输出格式

输出一行，表示老师至少需要准备的糖果数，如果不能满足小朋友们的所有要求，就输出 −1−1。

数据范围

1≤N≤1e5
1≤K≤1e5
1≤X≤5
1≤A，B≤N
输入数据完全随机。

输入样例：

5 7
1 1 2
2 3 2
4 4 1
3 4 5
5 4 5
2 3 5
4 5 1

输出样例：

11

思路

一、 求不等式组的可行解
建立超级源点需要满足的条件：从源点出发，一定可以走到所有的边。

步骤：
1. 先将每个不等式 xi≤xj+ck，转化成一条从 xj 走到 xi ，长度为 ck 的边。
2. 找到一个超级源点，使得该源点一定可以遍历到所有边
3. 从源点求一遍单源最短路

结果1：如果存在负环，则原不等式组一定无解。
结果2：如果没有负环，则 dist[i] 就是原不等式组的一个可行解。

二、 如何求最大值或者最小值，这里的最值指的是每个变量的最值
结论：如果求的是最小值，则应该求最长路；如果求的是最大值，则应该求最短路。

问题：如何转化 xi≤c ，其中 c 是一个常数，这类的不等式。

方法：建立一个超级源点0，然后建立 0 -> i 的边，长度是 c 即可。

以求 xi 的最大值为例：

求所有从 xi 出发，构成的多个形如如下的不等式 xi≤xj+c1≤xk+c2+c1≤⋅⋅⋅≤x0+c1+c2+⋅⋅⋅+cm(x0=0)

所计算出的上界，最终 xi 的最大值等于所有上界的最小值。

求 xi 的最小值 时则完全相反，求一个形如如下不等式链所计算出的下界，最终在所有下界里取最大值
xi≥xj+c1≥xk+c2+c1≥⋅⋅⋅≥x0+c1+c2+⋅⋅⋅+cm(x0=0)

转换成图论的问题，就是求 dist[i].

本题样例得到的图为

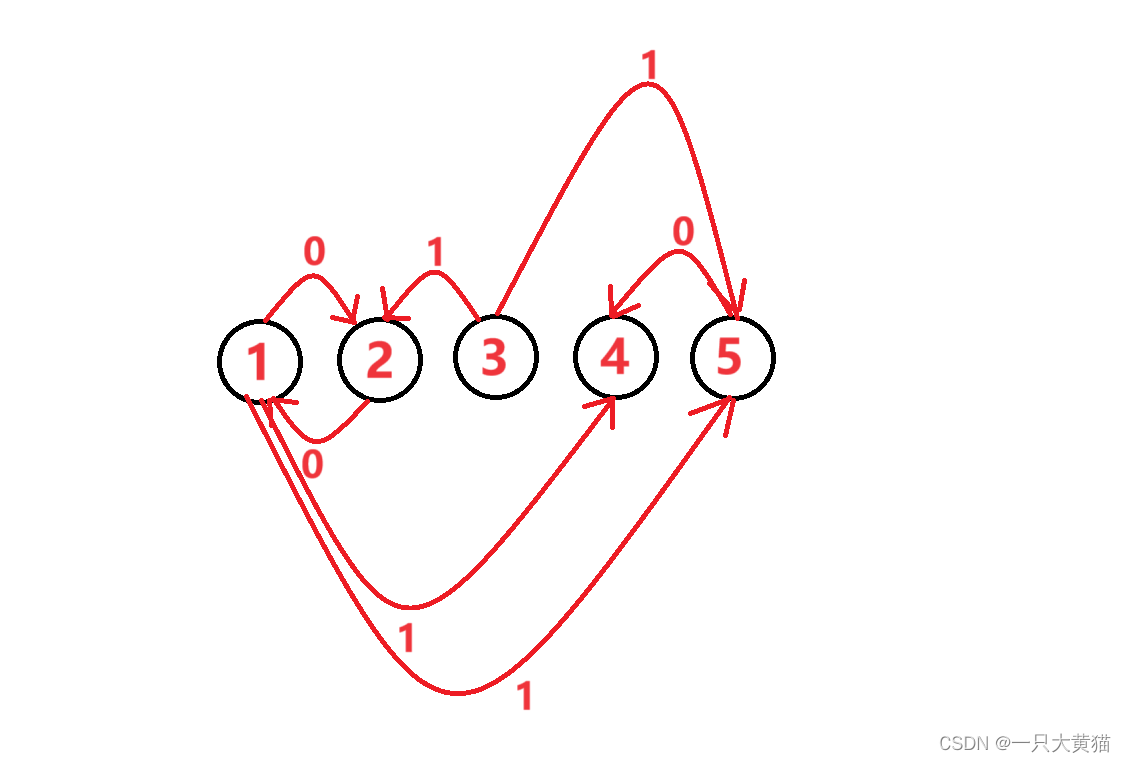
代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10;
int n,k;
int h[N],ne[N * 3],e[N * 3],w[N * 3],idx;
int dist[N];
bool st[N];
int cnt[N];void add(int a,int b,int c)
{ne[idx] = h[a],e[idx] = b,w[idx] = c,h[a] = idx ++;
}bool spfa()
{stack<int> q;for(int i = 1; i <= n; i ++) add(0,i,1);q.push(0);st[0] = true;while(!q.empty()){int t = q.top();q.pop();st[t] = false;for(int i = h[t]; ~i; i = ne[i]){int j = e[i];if(dist[j] < dist[t] + w[i]){dist[j] = dist[t] + w[i];cnt[j] = cnt[t] + 1;if(cnt[j] >= n + 1) return true;if(st[j]) continue;st[j] = true;q.push(j);}}}return false;
}int32_t main()
{cin >> n >> k;memset(h,-1,sizeof h);while(k --){int op,a,b;cin >> op >> a >> b;if(op == 1) add(b,a,0),add(a,b,0);if(op == 2) add(a,b,1);if(op == 3) add(b,a,0);if(op == 4) add(b,a,1);if(op == 5) add(a,b,0);}if(spfa()) cout << -1 << endl;else{int ans = 0;for(int i = 1; i <= n; i ++) ans += dist[i];cout << ans << endl;}return 0;
}

难度：中等

时/空限制：1s / 64MB

总通过数：7228

总尝试数：25419

来源：《信息学奥赛一本通》 , SCOI2011

算法标签 图论Tarjan算法有向图的强连通分量SPFA差分约束

题目来自：AcWing 1169. 糖果 - AcWing