内容包含笔者个人理解,如果错误欢迎评论私信告诉我
线性回归matlab部分参考了up主DR_CAN博士的课程
机器学习与概率论
在回归拟合数据时,根据拟合对象,可以把分类问题视为一种简答的逻辑回归。在逻辑回归中算法不去拟合一段数据而是判断输入的数据是哪一个种类。有很多算法既可以实现线性回归也可以实现逻辑回归。
| 线性回归 | 逻辑回归 | |
|---|---|---|
| 目的 | 预测 | 分类 |
| y ( i ) y^{(i)} y(i) | 未知 | (0,1) |
| 函数 | 拟合函数 | 预测函数 |
| 参数计算方式 | 最小二乘法 | 极大似然估计 |
如何实现概率上的分布?
在概率论中当拥有一组足够大样本数据时,那么这组数据的期望和方差会收敛于这个数据分布的期望和方差。
对基本的切比雪夫不等式, E ( I ∣ X − μ ∣ > α ) = P ( ∣ X − μ ∣ ≥ α ) ≤ D X α 2 E(I_{\left|X-\mu \right|}>\alpha )=P(\left|X-\mu \right|\ge\alpha)\le\frac{DX}{\alpha^2} E(I∣X−μ∣>α)=P(∣X−μ∣≥α)≤α2DX
由此出发可以推导出切比雪夫大数定律、伯努利大数定律,中心极限定理等概率论的基石公式。
那么假如现在我们有一组样本数据,样布数据来自某个未知分布。是否可以找到一个含参函数,可以百分百拟合样本服从的分布?
∃ f ( X ∣ θ ) ? ⇒ lim ε → 0 + P ( ∣ f ( X ) − x ∣ < ε ) = 1 \exists f(X|\theta )?\Rightarrow \lim_{\varepsilon \to 0^+} P(|f(X)-x|<\varepsilon )=1 ∃f(X∣θ)?⇒ε→0+limP(∣f(X)−x∣<ε)=1
从这个问题出发,在统计学上我们已经认识了矩估计、极大似然估计两种方法来计算这个函数中的具体参数。
对计算机来说是否有其他方法?
- 多层判断:如果样本分布在有限空间内,总可以找到一个符合分布的树状判断结构,一层一层递推判断并构建新分支,最后得到完整的符合分布的判断结构。
- 迭代学习:通过循环输入样本参数,计算函数的输出是否符合要求,再根据差距大小,调整函数构成和参数值,最后得到函数结果。
树状判断很好理解,那迭代学习如何实现:
首先是需要知道函数计算得到的分布和实际的分布之间的差距。继续上面的公式我们可以再加入一个函数,用来计算当前函数结果是否准确
l o s s ( f ( x ∣ θ ) − F ( X ) ) loss (f(x|\theta )-F(X)) loss(f(x∣θ)−F(X))
我们把这样的函数称之为代价函数,在深度学习中也可称之为损失函数。当有样本和真确分布的答案时(有监督学习)可以直接计算函数输出到实际的距离。对于没有正确答案的回归时,此时变为求解函数到所有样本点之间的距离:
L ( x , θ ) = 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) L(x, \theta) = \frac{1}{m}\sum_{i=1}^m(f(x^{(i)})-y^{(i)}) L(x,θ)=m1i=1∑m(f(x(i))−y(i))
当存在参数使得函数到所有样本距离最小的时候:
∃ θ ⇒ min L ( x , θ ) = min 1 m ∑ i = 1 m ( f ( x ( i ) ∣ θ ) − y ( i ) ) \exists\theta\Rightarrow\min L(x,\theta)=\min\frac{1}{m}\sum_{i=1}^m(f(x^{(i)}|\theta)-y^{(i)}) ∃θ⇒minL(x,θ)=minm1i=1∑m(f(x(i)∣θ)−y(i))
此时可以称之为找到了一个函数可以再概率上最大程度的拟合样本的分布情况。
机器学习中很多方法的目的就是,找到科学的方法,让计算机根据样本数据找到合适的函数 f 和合适的参数,并最终能够应用到新的场景对新样本做出预测或判断。
现在假设机器学习样本数据时直接使用上述的差值平均值作为代价,那如何求解参数来使差值最小?答案已经呼之欲出————梯度。 ∂ L ∂ θ = L ˙ ( x , θ ) = 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) ′ \frac{\partial L}{\partial \theta}=\dot{L} (x, \theta) = {\frac{1}{m}\sum_{i=1}^m(f(x^{(i)})-y^{(i)})}' ∂θ∂L=L˙(x,θ)=m1i=1∑m(f(x(i))−y(i))′ 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) θ ′ ⇒ 1 m ∑ i = 1 m ( f θ ′ ( x ( i ) ) − y ( i ) ) {\frac{1}{m}\sum_{i=1}^m(f(x^{(i)})-y^{(i)})}'_\theta \Rightarrow {\frac{1}{m}\sum_{i=1}^m(f'_\theta (x^{(i)})-y^{(i)})} m1i=1∑m(f(x(i))−y(i))θ′⇒m1i=1∑m(fθ′(x(i))−y(i))
计算梯度时,输入的样本是已知数据,需要变化的是函数的参数,通过计算代价函数对变量的梯度,就可以知道在输入样本的前提下,函数朝着什么方向变化参数能使输出的差值变小,此时计算机只需根据梯度更新参数。通过不断的循环这个步骤就达到了学习参数的目的。
通过上面的介绍,简单知道了学习的过程。实际上在机器学习中远没有这样简单,从函数结构,代价函数,到参数更新,输入输出等等,每一个环节都有着详细的内容和不同的方法来适应不同的数据场景。
机器学习与线性代数
矩阵的导数运算
在标量方程中偏导数的计算形式为: f ′ ( x ) = ∂ f ∂ x f'(x) = \frac{\partial f}{\partial x} f′(x)=∂x∂f 当二维的标量方程求偏导数时有: f ′ ( x 1 , x 2 ) = { d f ( x 1 , x 2 ) d x 1 d f ( x 1 , x 2 ) d x 2 f'(x_1, x_2)=\left\{\begin{matrix}\frac{\mathrm{d} f(x_1, x_2)}{\mathrm{d} x_1} \\\frac{\mathrm{d} f(x_1, x_2)}{\mathrm{d} x_2} \end{matrix}\right. f′(x1,x2)={dx1df(x1,x2)dx2df(x1,x2) 不妨可以将这样的偏导数写为向量形式,令 x ⃗ n = { x 1 , x 2 . . . . . . x n } \vec{x}_n = \left \{ x_1 , x_2 ......x_n \right\} xn={x1,x2......xn} 可以有n维方程的偏导数矩阵为: ∂ f ( x ⃗ ) ∂ x ⃗ = [ ∂ f ( x ⃗ ) ∂ x 1 ∂ f ( x ⃗ ) ∂ x 2 . . . ∂ f ( x ⃗ ) ∂ x n ] \frac{\partial f(\vec{x})}{\partial \vec{x}} =\begin{bmatrix}\frac{\partial f(\vec{x})}{\partial x_1} \\\frac{\partial f(\vec{x})}{\partial x_2} \\... \\\frac{\partial f(\vec{x})}{\partial x_n} \end{bmatrix} ∂x∂f(x)=⎣⎢⎢⎢⎡∂x1∂f(x)∂x2∂f(x)...∂xn∂f(x)⎦⎥⎥⎥⎤ 当偏导数矩阵的行数与原方程的维度相同时称之为分母布局,列数和原方程的维度相同时称之为分子布局。
很多时候在执行反向传播计算参数更新时就是由于布局模式的不同会导致求得的矩阵维度不同,而不同维度的矩阵往往都不能直接进行计算,导致程序出错。当然除了上面说的n*1维方程,也可以是向量方程组的形式: ∂ f ( x ⃗ ) ∂ x ⃗ = [ f 1 ( x ⃗ ) f 2 ( x ⃗ ) . . . f m ( x ⃗ ) ] x ⃗ = [ x 1 x 2 . . . x n ] \frac{\partial f(\vec{x})}{\partial \vec{x}} =\begin{bmatrix} f_1(\vec{x} ) \\f_2(\vec{x} ) \\... \\f_m(\vec{x} ) \end{bmatrix} \quad \vec{x} = \begin{bmatrix} x_1 \\x_2 \\... \\x_n \end{bmatrix} ∂x∂f(x)=⎣⎢⎢⎡f1(x)f2(x)...fm(x)⎦⎥⎥⎤x=⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤ 当使用分母布局时这样的向量方向方程组可以得到偏导数矩阵: ∂ f ( x ⃗ ) m ∂ x ⃗ n = [ ∂ f ( x ⃗ ) ∂ x 1 ∂ f ( x ⃗ ) ∂ x 2 . . . ∂ f ( x ⃗ ) ∂ x n ] = [ ∂ f 1 ( x ⃗ ) ∂ x 1 ∂ f 2 ( x ⃗ ) ∂ x 1 . . . ∂ f m ( x ⃗ ) ∂ x 1 . . . . . . . . . . . . ∂ f 1 ( x ⃗ ) ∂ x n . . . . . . ∂ f m ( x ⃗ ) ∂ x n ] n × m \frac{\partial f(\vec{x})_m}{\partial \vec{x}_n} =\begin{bmatrix} \frac{\partial f(\vec{x})}{\partial x_1} \\\frac{\partial f(\vec{x})}{\partial x_2} \\... \\\frac{\partial f(\vec{x})}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1(\vec{x})}{\partial x_1} &\frac{\partial f_2(\vec{x})}{\partial x_1} &... &\frac{\partial f_m(\vec{x})}{\partial x_1} \\ ... &... &... &... \\ \frac{\partial f_1(\vec{x})}{\partial x_n} &... &... &\frac{\partial f_m(\vec{x})}{\partial x_n} \end{bmatrix}_{n\times m} ∂xn∂f(x)m=⎣⎢⎢⎢⎡∂x1∂f(x)∂x2∂f(x)...∂xn∂f(x)⎦⎥⎥⎥⎤=⎣⎢⎡∂x1∂f1(x)...∂xn∂f1(x)∂x1∂f2(x)...............∂x1∂fm(x)...∂xn∂fm(x)⎦⎥⎤n×m 但一般来说会用更加简洁的方式表达矩阵导数: x ⃗ = [ x 1 . . . x m ] , A m × n ⇒ ∂ A x ⃗ ∂ x ⃗ = A T \vec{x}=\begin{bmatrix}x_1 \\... \\x_m \end{bmatrix} \quad ,A_{m\times n} \quad \Rightarrow \frac{\partial A\vec{x} }{\partial \vec{x}} =A^T x=⎣⎡x1...xm⎦⎤,Am×n⇒∂x∂Ax=AT
当原函数存在平方形式时转换为二次型计算: ∂ x ⃗ T A x ⃗ ∂ x ⃗ = A x ⃗ + A T x ⃗ \frac{\partial \vec{x}^TA\vec{x} }{\partial \vec{x}} =A\vec{x}+A^T\vec{x} ∂x∂xTAx=Ax+ATx 值得注意,在分析系统建模的过程中A可能会得到一个对角型矩阵,此时转置等于本身。
例:线性回归中的矩阵计算
在线性回归中使用的公式主要有: ∂ A x ⃗ ∂ x ⃗ = A T \frac{\partial A\vec{x} }{\partial \vec{x}} =A^T ∂x∂Ax=AT ∂ x ⃗ T A x ⃗ ∂ x ⃗ = A x ⃗ + A T x ⃗ \frac{\partial \vec{x}^TA\vec{x} }{\partial \vec{x}} =A\vec{x}+A^T\vec{x} ∂x∂xTAx=Ax+ATx
假设有一组二维数据,x与y不相互独立,可以尝试计算得到这组数据的线性回归解。
| x | 75 | 71 | 83 | 74 | 73 | 67 | 79 | 73 | 88 | 79 | 73 | 88 | 81 | 78 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 183 | 175 | 187 | 185 | 176 | 176 | 185 | 191 | 195 | 185 | 190 | 185 | 75 | 71 |
x是体重,y是身高。可以找到一个估计的函数来表示x-y之间的关系 y ^ = a x + b \hat{y} = ax+b y^=ax+b 基于上面概率论的部分,此时我们可以先计算所有样本数据到待估计的函数之间的距离,同时为了保证差值恒为正数便于计算,可以得到: [ y 1 − ( a x 1 + b ) ] 2 [ y 2 − ( a x 2 + b ) ] 2 . . . [ y n − ( a x n + b n ) ] 2 \begin{matrix}\left [ y_1-(ax_1+b) \right ]^2 \\\left [ y_2-(ax_2+b) \right ]^2 \\... \\\left [ y_n-(ax_n+b_n) \right ]^2 \end{matrix} [y1−(ax1+b)]2[y2−(ax2+b)]2...[yn−(axn+bn)]2 把这个差值写成一个函数的形式有: J = ∑ i = 1 n [ y i − ( a x i + b ) ] 2 J=\sum_{i=1}^{n} \left [ y_i-(ax_i+b) \right ]^2 J=i=1∑n[yi−(axi+b)]2这里的J函数就称之为代价函数,平方项的计算就是最小二乘法。通过计算J函数对a和对b的偏导数可以求出J在理论上最小的点,此时得到的a和b就是线性回归的数学最优解。
但是上面的计算过程对于计算机来所不容易编程和求解,所以可以使用线性代数的工具将其转化为矩阵计算: y ⃗ = [ y 1 , y 2 , . . . , y n ] T x ⃗ = [ x 1 x 2 . . . x n 1 1 1 1 ] T \vec{y}= [y_1, y_2, ...,y_n]^T \quad \vec{x}=\begin{bmatrix} x_1 &x_2 &... &x_n \\ 1 & 1 &1 &1 \end{bmatrix} ^T y=[y1,y2,...,yn]Tx=[x11x21...1xn1]T 此时有: y ⃗ ^ = x ⃗ × [ a b ] ⇒ J = [ y ⃗ − y ⃗ ^ ] T × [ y ⃗ − y ⃗ ^ ] \hat{\vec{y}} = \vec{x}\times \begin{bmatrix} a \\b \end{bmatrix} \Rightarrow J=[\vec{y}-\hat{\vec{y}}]^T\times [\vec{y}-\hat{\vec{y}}] y^=x×[ab]⇒J=[y−y^]T×[y−y^] ⇒ = y ⃗ T y ⃗ − 2 y ⃗ T x ⃗ θ ⃗ + θ ⃗ x ⃗ T x ⃗ θ ⃗ θ ⃗ = [ a , b ] T \Rightarrow =\vec{y}^T\vec{y}-2\vec{y}^T\vec{x}\vec{\theta}+\vec{\theta}\vec{x}^T\vec{x}\vec{\theta} \quad \vec{\theta}=[a, b]^T ⇒=yTy−2yTxθ+θxTxθθ=[a,b]T ⇒ ∂ J ∂ θ ⃗ = 0 − 2 ( y ⃗ T x ⃗ ) + 2 x ⃗ T x ⃗ θ ⃗ = 0 \Rightarrow \frac{\partial J}{\partial \vec{\theta }} =0-2(\vec{y}^T\vec{x})+2\vec{x}^T\vec{x}\vec{\theta }=0 ⇒∂θ∂J=0−2(yTx)+2xTxθ=0 ⇒ θ ⃗ = ( x ⃗ T x ⃗ ) − 1 x ⃗ T y ⃗ ⇒ θ ⃗ = [ 127.6 , 0.71 ] T \Rightarrow \vec{\theta } =(\vec{x}^T\vec{x})^{-1}\vec{x}^T\vec{y} \Rightarrow \vec{\theta }=[127.6, 0.71]^T ⇒θ=(xTx)−1xTy⇒θ=[127.6,0.71]T 至此求得了这组数据通过最小二乘法得到的解析解。那么计算如何通过迭代来模拟上面的计算过程呢?这里就十分简单了,先给定一个参数的初始值,然后计算代价函数对参数的梯度,这里上面已经推导过向量函数的导数计算,所以可以直接有梯度为: ∇ x = x ′ ⃗ × ( − y + x ⃗ × θ 0 ⃗ ) θ 0 为 初 值 , x ′ ⃗ = [ x 1 x 2 . . . x n 1 1 1 1 ] T \nabla x = \vec{x'}\times (-y+\vec{x}\times \vec{\theta_0 })\quad \theta_0为初值,\vec{x'}=\begin{bmatrix} x_1 &x_2 &... &x_n \\ 1 & 1 &1 &1 \end{bmatrix} ^T ∇x=x′×(−y+x×θ0)θ0为初值,x′=[x11x21...1xn1]T
使用matlab计算解析解
%% 使用最小二乘法计算数据的线性回归最优解clear all;
clc;x = [75, 71, 83, 74, 73, 67, 79, 73, 88, 80, 81, 78, 73, 68, 71]';
y = [183, 175, 187, 185, 176, 176, 185, 191, 195 ,185, 174, 180, 178, 170, 184]';X =[ones(15, 1), x]; %生成x的转置扩充数据X_T = transpose(X); %转置
a_start = inv(X_T * X)*X_T*y; % inv计算矩阵的拟,得到线性估计的参数a和b,这里是解析解x_draw = 65:0.1:90;
scatter(X(:, 2), y, 80, "r"); % 原始数据的散点图
hold on;
plot(x_draw, a_start(2)*x_draw+a_start(1)); % 解析解的线性回归结果
grid on;
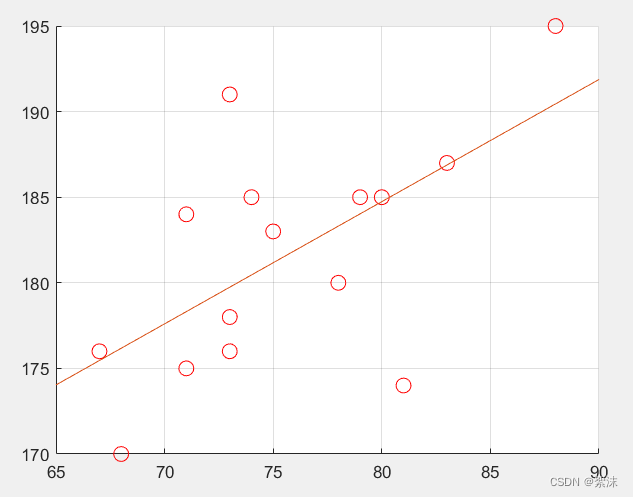
上图是最小二乘法的最优计算结果。
使用matlab通过梯度下降迭代计算解
%% 使用ML的梯度下降法迭代计算参数
clear all;
clc;x = [75, 71, 83, 74, 73, 67, 79, 73, 88, 80, 81, 78, 73, 68, 71]';
y = [183, 175, 187, 185, 176, 176, 185, 191, 195 ,185, 174, 180, 178, 170, 184]';%% 解析解
X =[ones(15, 1), x]; %生成x的转置扩充数据X_T = transpose(X); %转置
a_start = inv(X_T * X)*X_T*y; % inv计算矩阵的拟,得到线性估计的参数a和b,这里是解析解x_draw = 65:0.1:90;
scatter(X(:, 2), y, 80, "r"); % 原始数据的散点图
hold on;
plot(x_draw, a_start(2)*x_draw+a_start(1)); % 解析解的线性回归结果
grid on;%% 梯度下降回归解
% 1、定义参数,初始化矩阵% 2、while 循环 y = y - lr * x'ab_start = [100 ; 2]; % 设置一个初始值% 学习率learning_reate = 0.00002; %learning_reate = [0.001 0; 0 0.00001]; % 使用二阶学习率适应原始数据的倍率% 迭代for i = 1:100000ab_start = ab_start - learning_reate * X_T *( -y +X* ab_start); % 计算代价函数对参数矩阵的梯度,用原参数减学习率乘梯度end

此时可以看出ab_start 作为迭代计算得到的结果已经拟合于解析解算的结果了。

调制和QSSK(正交空间位移键控)调制误码率对比。)





:Git常用命令)

】为什么 Nios® V/g 处理器无法从指令紧耦合内存 (TCM) 启动?)



)


)


