欢迎来到博主的专栏——C语言数据结构
博主id：代码小豪

单链表

顺序表是一个物理结构上连续（即数据在内存中连续存储）的线性表，这种特性让顺序表的访问非常方便，但是顺序表有一个缺点，就是当我们在顺序表插入或删除数据时，需要较为繁杂的指令执行（时间复杂度O（N））。

为什么会这样呢？因为数据的连续的存储结构虽然为顺序表的数据访问带来了便利，但是当顺序表需要插入元素时，联系的存储结构是没有多余的空间留给待插入的元素的，只能将顺序表中的后继数据依次向后移动，才能腾出空间让数据插入。

当顺序表删除一个元素时，不能只是单纯的将这个元素移除，因为移除一个元素之后，连续存储的结构就被破坏掉了，为了保持顺序表的结构，只能将后面元素依次向前移动。

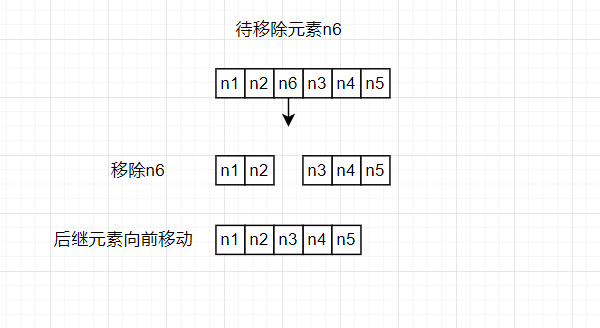
如果我们编写的程序需要频繁的对线性表进行删除、插入的操作时，使用顺序表的数据结构会让程序的运行时间变长。为了解决这个问题，我们需要一个适合插入和删除元素的线性表。

根据上面对顺序表的分析，我们知道导致顺序表插入元素和删除元素的操作如此繁杂的原因就是，顺序表需要时刻保持连续储存的内存结构。

那么解决思路来了，如果我们插入元素时，这些元素不需要连续的存储结构，也能有着线性的逻辑结构，那么不就能实现一个插入和删除操作不繁杂的线性表了吗？那么有一个问题就诞生了，如何将不连续存储的数据彼此之间联系起来呢？

不连续存储的线性表

假如你是一个来到广州的游客。你打算去以下几个地方：广州塔、北京路、长隆。如果这几个地方。如果它们顺序的排列在广州站附近就好了，这样子你一出站就能游玩所有的地方，但是现实当中这绝对不可能。

如何达到我们想去的景点呢？我想我会先打开gps，然后定位我打算去的地方，至于交通工具的选择我想就因人而异了。但是不可否认的事，我得先知道景点在哪，我才能去。

那么，C语言中能够定位数据的gps是什么呢？没错，就是指针。如果线性表中的所有元素，使用指针联系起来，那么，这些数据元素就不需要在内存中连续存储了。

那么这种联系的方式是什么呢？我们再以现实举例，如果我想要从广州站导航到广州塔，gps需要得到什么？是不是需要得到我的当前地址（广州站），再得到广州塔的地址，最后给出路线。跟着导航我们就能达到广州塔。

回到线性表，如果一个数据中，存储着下一个数据的地址。那么当我们得到一个数据时，是不是就能找到这个数据的后继元素？

理论形成，开始实践

单链表

根据前面的判断可以得出，这个线性表中的元素不仅仅要存储元素本身的数据，还要存储指向下一个元素的指针，这样子才能通过指针找到下一个元素。

这个线性表的数据关系应该是这样的

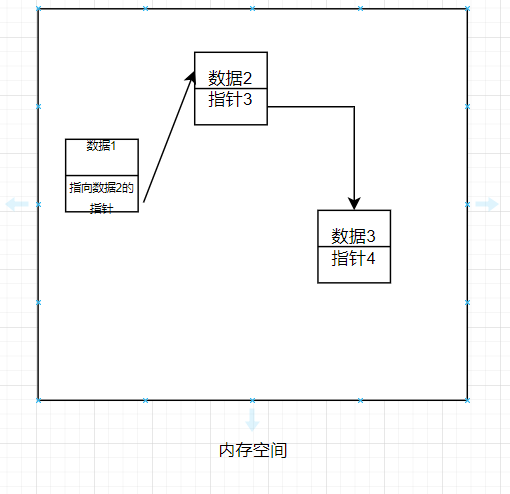
可以发现这种线性表是不需要顺序存储结构的，通过指针完成元素与后继元素的联系，实现线性的逻辑结构。

既然这种线性表的存储结构是无规律的，那么我们就忽视存储结构，直接抽象出这些数据的逻辑结构。

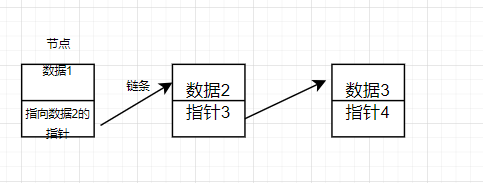
观察上图，我们发现这种关系图有点像那种打草结，将整个顺序表看做是一个藤蔓，如果想要插入一个数据，就好比在藤蔓上打个结，有多少个元素就有多少个结。所以将这种元素称为节点。而草结与草结之间还有一个藤条联系着，就可以看做数据与数据之间有一个链条联系着。

所以这种数据结构被称为，链表（链条作为联系的顺序表）。链表中的数据被叫做节点。

目前先来介绍的是单链表，单链表是由单向链条而得名，比如图中得到一个数据只能访问后继元素，这种是单向链条，而数据不仅能访问后继元素，也能访问前置元素的被称为双向链表。

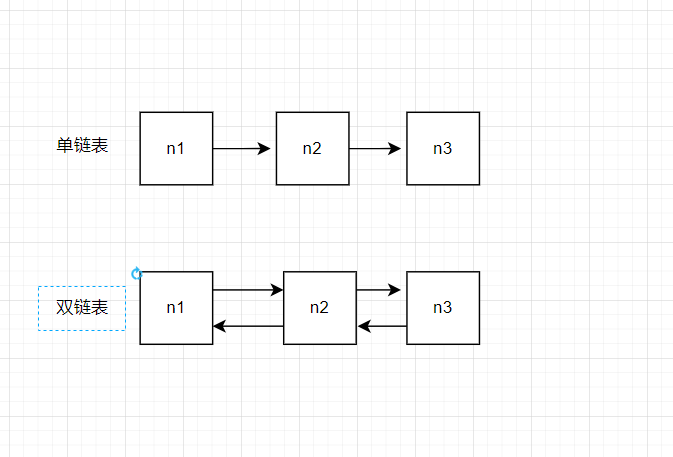
单链表的结构

单链表中的数据要满足两个条件，一是能储存数据本身、二是能存储指向下一个数据的指针。那么C语言中的什么数据类型能够做到这一点呢？首先C语言中的内置类型（int、float、char）肯定是不行的，因为它们只能做到存储元素本身的数据。所以我们要将目光转向结构体类型。

单链表结点的结构体类型如下：

typedef int SLData;
typedef struct SLlistNode
{SLData data;struct SLlistNode* next;
}Node;

data是节点元素存储本身的数据，next是指向下一个结点元素的指针。我们可以手动的写出一个链表。

	Node* node1 = malloc(sizeof(Node));Node* node2 = malloc(sizeof(Node));Node* node3 = malloc(sizeof(Node));Node* node4 = malloc(sizeof(Node));node1->data = 1;node2->data = 2;node3->data = 3;node4->data = 4;node1->next = node2;node2->next = node3;node3->next = node4;node4->next = NULL;

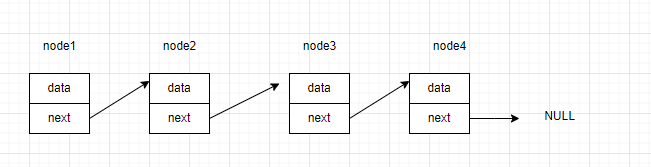
线性表中的元素特征如下：除表头和表尾外每个元素都有一个前驱元素和后继元素，表头元素无前驱、表尾元素无后继。

所以node4作为表尾是没有后继元素的，所以node4->next’不指向内存中的任何位置，置为NULL

打开vs中的调试操作，可以发现链表的数据结构如下：

可以发现、只需要有node1，就可以通过访问next找到其余结点的数据。

头指针

前面的操作一经发现node1的一个重要作用，就是只要能获取node1的位置，就能找到整个链表的数据。

我们将node1称为单链表的第一个结点、指向第一个结点的指针称为头指针、这样子在调用单链表的操作函数时、只需要传入头指针、就能对链表中的所有节点进行访问。

单链表的操作

打印单链表

为了方便调试和查看单链表、我们可以创建一个打印单链表的函数，前面已经提到了通过头指针可以访问整个链表的特性，所以这个函数只需要一个参数，那就是传入单链表中的头指针

void printSList(Node* phead);

那么该如何遍历整个单链表、访问整个单链表的数据呢？

可以创建一个临时指针pcur，让pcur通过next指针循环访问整个链表。

循环的结束标志就是访问完链表的表尾，而链表中的表尾元素的next被置为NULL。所以判断结束的条件便是pcur=NULL

函数实现的代码如下：

void printSList(Node* phead)
{Node* pcur = phead;while (pcur){printf("%d->",pcur->data);pcur = pcur->next;}printf("NULL\n");
}

以上面创建的链表为例，调用打印链表的函数

	printSList(node1);

执行结果如下：

空链表

如果一个链表中没有任何一个节点，就将这个链表称为空链表。

前面提到了头指针是指向链表中第一个节点的指针。但是空链表的头指针应该指向哪儿呢？

头指针是指第一个节点的指针，它的存在是标记一个链表的表头。将头指针传入函数中进行调用，可以对整个链表进行操作。这就说明了一个头指针，是一个单链表的化身。任何一个单链表，都需要有一个头指针作为该单链表的标志。

那么空链表是不是一个单链表，当然是了。这就说明空链表也应该有一个头指针，这个头指针应该指向哪儿呢？空链表是没有第一个节点的，那就只好将头指针置为NULL了。

那么可以得出一个结论，将一个头指针置为NULL，说明该头指针对应的是一个空链表。

单链表的插入

尾插法

在单链表中的表尾该如何插入元素呢？我们知道节点的next指针是指向后继元素的，而尾节点的next指针指向NULL。所以插入元素的方法为：将待插入节点作为当前尾节点的后继元素（即尾节点->next指向待插入元素），并将待插入节点的后继节点位置置为NULL。

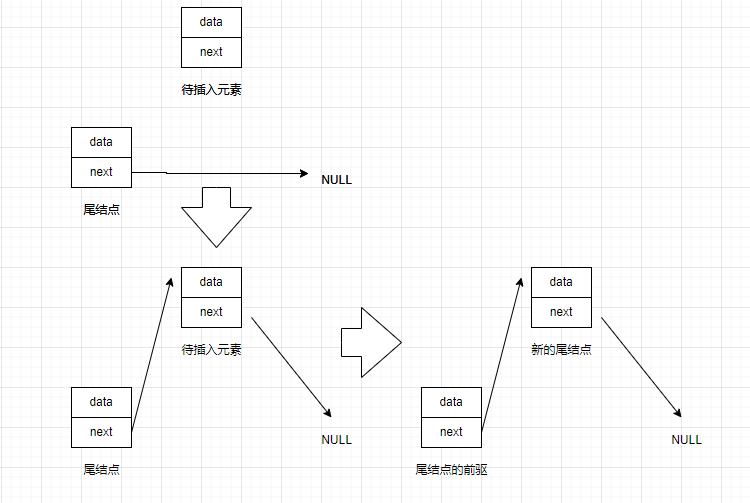
那么我们待解决的问题就是如何遍历珍整个单链表找到尾结点了，尾结点的next指向NULL。我们可以通过这个条件来判断当前节点是否为尾结点。

尾插法的函数原型的参数应该有两个，一是待尾插的单链表是哪个，而是插入的节点数据是什么。找到单链表的方式很简单，只需要传入该链表的头指针就行了。

于是函数原型如下：

void SLlistDataPushBack(Node** pphead, SLData n);

头指针的数据类型是Node*，这里将函数参数作为二级指针的原因如下：

（1）尾插法在特殊情况下是需要对头指针进行修改的，比如当传入的单链表为空链表时，需要将插入的节点设置为第一个节点的，即头指针要从NULL变成指向第一个节点的指针。

（2）既然头指针的数据类型是一个一级指针，那么函数的参数如果也是一个一级指针的话，就不能对头指针进行修改了，因为函数的参数，是实参的一份临时拷贝。也就是说对函数中的头指针进行修改，是不会对传入函数的头指针进行操作的。

（3）那么想要对头指针进行数据修改，就需要将形参升级为二级指针，通过解引用二级指针，才能实现对一级指针的修改。

从这里也能得到一个推论，如果一个单链表的操作函数涉及了头指针的修改的话，就需要将接收这个头指针的形式参数改为一个二级指针。

那么通过上述分析我们已经知道了尾插法在操作时可能会遇到的两种情况。
（1）传入的链表为非空链表时，处理方法如下

（2）传入的链表为空时，解决方法如下：

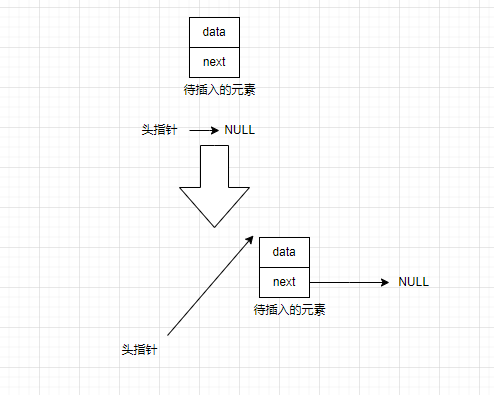
于是尾插法的函数实现如下：

void SLlistDataPushBack(Node** pphead, SLData n)//尾插法
{assert(pphead);Node* pcur = *pphead;Node* pend = malloc(sizeof(Node));//创建待插入元素pend->next = NULL;//尾插法中的待插入元素无后继pend->data = n;if (*pphead==NULL)//判断链表是否为空{(*pphead = pend);//将头指针指向新节点return;}while (pcur->next)//判断是否为尾节点{pcur = pcur->next;}pcur->next = pend;//将待插入的元素作为当前尾结点的后继，完成尾插return;
}

可以用前面写的代码进行测试一下。比如

	Node* plist = NULL;SLlistDataPushBack(&plist, 1);SLlistDataPushBack(&plist, 2);SLlistDataPushBack(&plist, 3);SLlistDataPushBack(&plist, 4);printSList(plist);

运行结果如下：

头插法

将节点插入至链表的表头称为头插法，节点被插入表头的方法如下
(1)将头指针指向新插入的节点
(2)将原先的第一个节点变成新插入的节点的后继元素

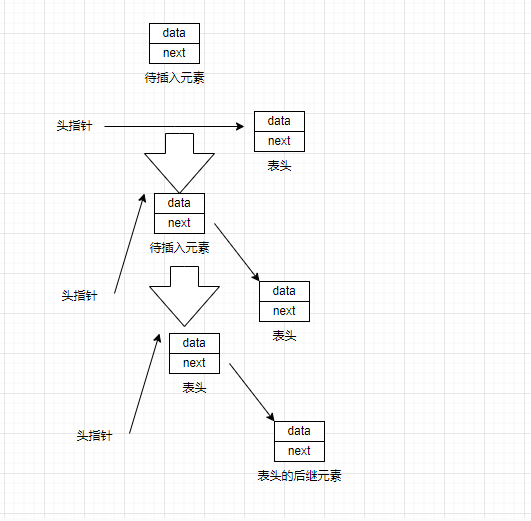
这个函数中会将头指针进行修改，前面提到了如果函数中出现了修改头指针的情况，那么函数中的形式参数应该设置为头指针的二级指针，这样才能通过解引用操作对头指针进行修改

还要注意一个特殊情况，那就是传入的链表为空链表的情况。如果传入的链表为空链表，那么新插入的节点没有后继，那么这个节点的next应该置为NULL。

于是函数的原型如下：

void SLlistDataPushFront(Node** pphead, SLData n);

根据上述的原理，函数的实现如下：

void SLlistDataPushFront(Node** pphead, SLData n)
{assert(pphead);//检测头指针的二级指针的合法性Node* pstart = malloc(sizeof(Node));//待插入的节点pstart->data = n;if (*pphead==NULL)//检测链表是否为空表{pstart->next = NULL;*pphead = pstart;return;}pstart->next = (*pphead);//注意这两行代码顺序不能互换*pphead = pstart;
}

注意这两行代码：

pstart->next = (*pphead);
*pphead = pstart;

不能让*pphead先等于pstart，再将pstaet的后继元素设置为（*pphead）,原因交给大家思考。

将函数进行测试，方法如下：

	SLlistDataPushFront(&plist, 5);SLlistDataPushFront(&plist, 6);SLlistDataPushFront(&plist, 7);SLlistDataPushFront(&plist, 8);printSList(plist);

单链表的查找

单链表的查找就很简单了，根据要查找数据项，将整个链表的元素遍历一遍，如果找到就返回一个指向该节点的指针、如果没有找到就返回NULL

函数原型如下：

Node* SLlistFind(Node* phead, SLData n)

具体实现如下：

Node* SLlistFind(Node* phead, SLData n)
{Node* pcur = phead;while (pcur){if ((pcur->data) == n)return pcur;pcur = pcur->next;}return NULL;
}

任意位置处的节点插入

在链表中插入的位置可分为三种
（1）插入表头
（2）插入表尾
（3）插入其他位置

其中前面两种方法都已经说过了，现在来了解一下其他位置的数据插入。

我们要在两个数据之间插入元素，假设要插入的位置为第i+1项，那么原本在第i+1项的节点就要成为新插入节点的后继节点，而第i项节点要成为新插入元素的前驱节点。

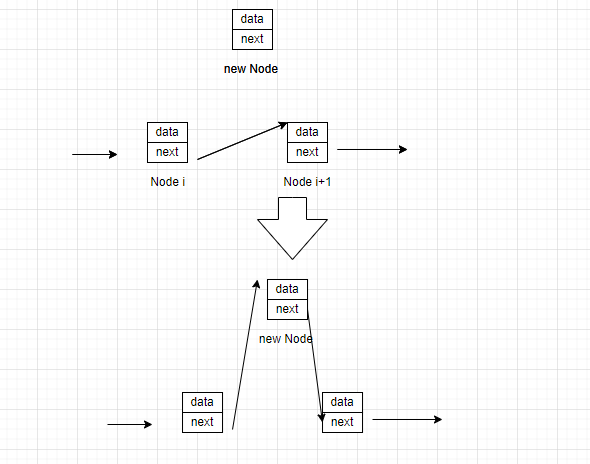
写成代码应该是这样的

newnode->next=nodei->next;
nodei->next=new->node;

要注意这两行的顺序。 如果数据要插入表头，表尾、或者传入空表时，可以用头插法\尾插法的方式实现。

那么现在就剩第二个问题了，就是如何确定待插入元素的位置，我们前面定义了一个查找节点的函数，通过查找数据项确定元素位置。还有一种情况是指定位置插入节点，即不管第3个节点的数据是什么，我这个数据都要插入第三个节点（当然，没有第三个节点位置的另算）。

总之根据实现的要求，寻找位置的方式都是各种各样的，但是插入节点的原理是不变的，这里先来讲解通过指针的方式寻找插入位置的方法（即通过寻找数据项确定位置，因为前面定义了函数嘛）、

void SLlistInsert(Node** Pphead, Node* pos, SLData n);

（1）pphead是链表的头指针的二级指针
（2）pos是待插入节点的地址位置（地址位置可以通过前面编写的查找节点的函数来确定。）
（3）n是待插入节点的数据

void SLlistInsert(Node** pphead, Node* pos, SLData n)
{assert(pphead);if (pos == (*pphead))//第一节点就是要插入的位置{SLlistDataPushFront(pphead, n);return;}Node* pcur = *pphead;Node* newnode = malloc(sizeof(Node));newnode->data = n;while (pcur->next != pos)//找到对应位置才会退出循环{pcur = pcur->next;}newnode->next = pcur->next;pcur->next = newnode;
}

通过测试，发现该函数插入表尾不需要使用尾插法。

实际上根据不同的实现要求，所有写链表的程序都是不唯一的，但是插入节点的原理都是类似。这里需要大家对链表有一个比较深的理解。博主只是列举其一、但是并非唯一的实现方法。

比如有些程序要求对指定位置之前插入节点，有的要求对指定位置之后插入节点，那么此时就要具体问题具体分析了。但是插入的原理不变。只是如何定位的差异。

单链表节点的删除

链表中的节点被删除，节点中的前驱元素和后继元素的关系就被改变了，被删除的节点的前驱节点应该直接指向被删除的后继节点，这样子链表就不会在访问该节点了。

又由于该节点是由动态内存函数开辟的空间，因此该节点被删除时，应该被释放掉。

我们还是使用SLlistFind函数确定删除的节点位置pos。

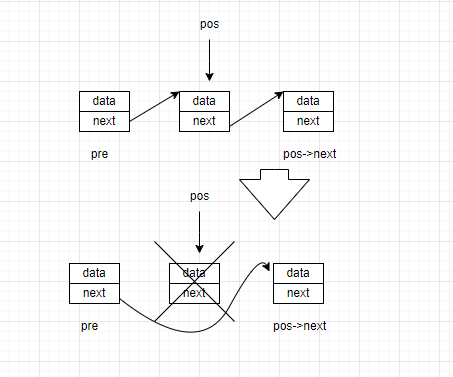
从图中可以发现，为了定位到pos的前驱节点，还需要创建多一个pre的临时指针。

函数原型如下：

void SLlistDelete(Node** pphead, Node* pos);

前面将述的方法都是建立在被删除的节点有前驱节点和后继节点的情况下，如果被删除的节点没有前驱节点（第一个节点），就不能用上述方法。

我们针对这个条件在设计一道程序，如过头指针与被删除节点的地址一致，我们就将头指针指向删除节点的后继节点，再释放掉第一个节点的空间。

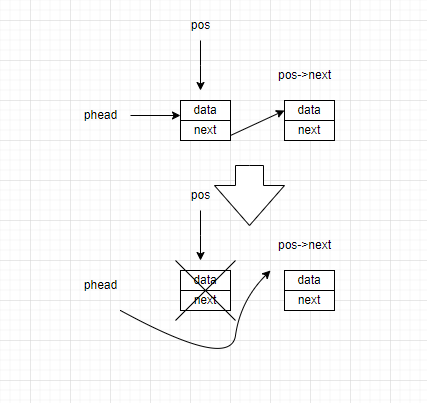
函数的实现如下：

void SLlistDelete(Node** pphead, Node* pos)
{assert(pphead);assert(*pphead);if (*pphead == pos)//删除第一个节点{*pphead = (*pphead)->next;free(pos);return;}Node* prev = *pphead;//删除其他位置的节点while (prev->next != pos){prev = prev->next;}prev->next = pos->next;free(pos);
}

销毁链表

如果某个链表在程序当中已经不再使用了，由于链表是由动态内存开辟的，要将这个链表的内存空间释放。

释放的方法如下：将链表从第一个节点开始，通过循环将整个链表的节点进行删除。

函数原型：

void SLlistDestory(Node** pphead);

销毁链表的原理也很简单，通过节点之间的联系将整个链表循遍历一遍，每经过一个节点，就将该节点释放。循环结束后将头指针置为NULL

函数的实现如下：

void SLlistDestory(Node** pphead)
{assert(pphead);Node* pcur = *pphead;Node* pnext ;while (pcur){pnext = pcur->next;free(pcur);pcur = pnext;}*pphead = NULL;
}