前言
最短路问题真的很重要很重要希望大家都能够完全掌握所有最短路算法!!
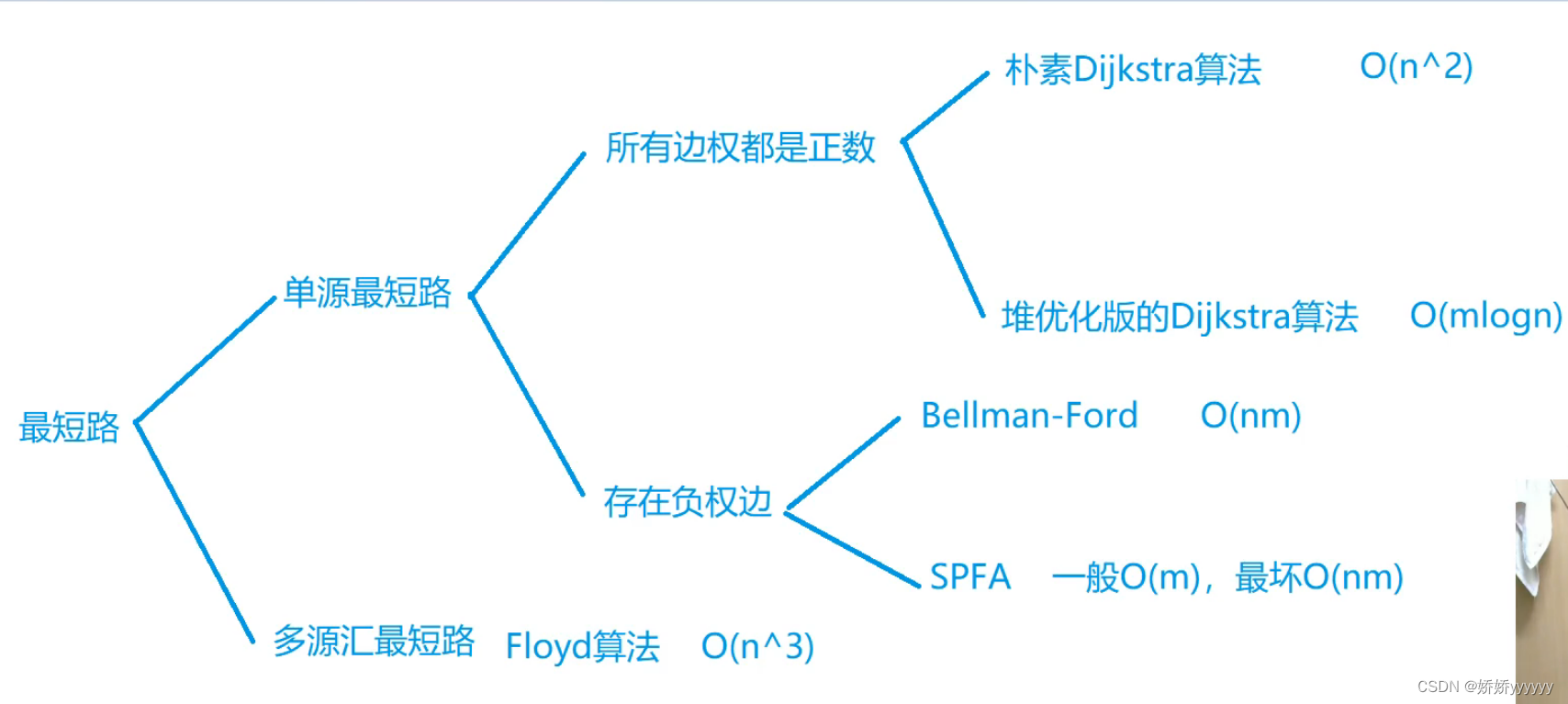
一、最短路问题的分类
Dijkstra:
Dijkstra算法是一种著名的图算法,主要用于求解有权图中的单源最短路径问题。它由荷兰计算机科学家艾兹赫尔·戴克斯特拉(Edsger Wybe Dijkstra)在1956年首次提出。Dijkstra算法的核心思想是通过以下步骤逐步构建最短路径树:
初始化:创建一个空白的最短路径字典,其中每个节点的距离设置为无穷大,起始节点的距离设置为0。
标记已访问节点:创建一个已访问节点集合,并将所有节点都加入这个集合。
更新距离:对于未被访问的节点,从其未被访问的邻居中选择距离当前节点最近的邻居,将其标记为已访问,并且更新该邻居节点的距离。
重复上述步骤:直到所有节点都被访问,此时已经得到了从起始节点到所有其他节点的最短路径。
Dijkstra算法的特点在于它能够处理图中的负权边,但通常会忽略这些边,因为它们不会影响最终的路径长度计算。如果图中存在负权边,可能需要使用其他的图算法,如Bellman-Ford算法。此外,Dijkstra算法的时间复杂度通常是O(V^2),其中V是节点数量,但如果使用优先队列来优化,时间复杂度可以减少到O(Elog(V)),其中E是边数。1
在实际编程实现时,可以使用不同的数据结构和算法来实现Dijkstra算法,以提高效率。例如,可以使用优先队列或堆来加速松弛操作,从而减少总体时间复杂度。2
总结一下,Dijkstra算法的主要优点是可以有效地解决单源最短路径问题,并且在大多数情况下不需要考虑负权边的影响。它在多个领域有着广泛的应用,包括路线规划、网络路由、资源分配等。
Bellman-Ford算法:
贝尔曼-福特算法(Bellman-Ford Algorithm)是一种用于求解单源最短路径问题的算法,由理查德·贝尔曼(Richard Bellman)和莱斯特·福特(Lester Ford)共同创立。该算法能够处理图中的负权边,并具有简单的实现方式和较高的时间复杂度。贝尔曼-福特算法的核心思想是通过多次松弛操作来确定所有可能的最短路径。每次迭代中,算法会更新所有节点的距离,确保它们符合“三角不等式”,即任意两点间的距离加上第三者的重量小于或等于这两点间距离之和。
尽管贝尔曼-福特算法在处理带负权边的最短路径问题上表现良好,但在某些情况下可能会遇到困难,如当图中存在负权环路时,可能会导致无法找到任何有效的最短路径。此外,虽然它可以处理负权边,但其时间复杂度为 \( O(VE) \),其中 \( V \) 是顶点的数量,\( E \) 是边的数量,这使得它在实践中可能不是最佳选择。
总结来说,贝尔曼-福特算法的主要优点包括支持负权边和简单性,而其主要缺点在于高的时间复杂度。为了提高效率,算法可以进行一些优化措施。需要注意的是,贝尔曼-福特算法有时也被称作 Moore-Bellman-Ford 算法,因为它还涉及到了另一位科学家 Edward F. Moore 的贡献。
SPFA算法:
SPFA算法
SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环
Floyd算法:
floyd算法
Floyd算法,也被称为弗洛伊德算法或插点法,是一种解决加权图中顶点间最短路径问题的算法。它可以处理有向图或负权图(但不能存在负权回路),并同时用于计算有向图的传递闭包。Floyd算法的名称来源于其创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德。
Floyd算法的核心思想是利用动态规划技术来构建一个路径矩阵,这个矩阵包含了图中所有顶点对之间的最短路径长度。算法的基本步骤包括初始化路径矩阵、进行多次更新操作以及最终获取任意两点之间的最短路径。
具体来说,算法会创建两个矩阵:一个存储了顶点对之间的距离,另一个存储了这些距离的逆。在每一次迭代中,都会根据已有的信息更新这两个矩阵。这个过程涉及到多个嵌套的for循环,直到所有的路径都被计算出来为止。
Floyd算法的时间复杂度和空间复杂度分别为O(n^3)和O(n^2),这意味着它在处理大规模网络图时会比较耗时。此外,虽然算法本身不需要回溯路径的具体信息,但它确实可以用来构造出最短路径的详细列表。
总结一下,Floyd算法的主要特点和应用场景如下:
适用范围:适用于有向图或负权图,不能有负权回路。
时间复杂度:O(n^3),即n³次操作。
空间复杂度:O(n^2),即n²个变量。
主要用途:求解任意两点间的最短路径,也可以用于计算传递闭包。
其他应用:在某些情况下,可以用于查找关系的传递闭包。
二、例题
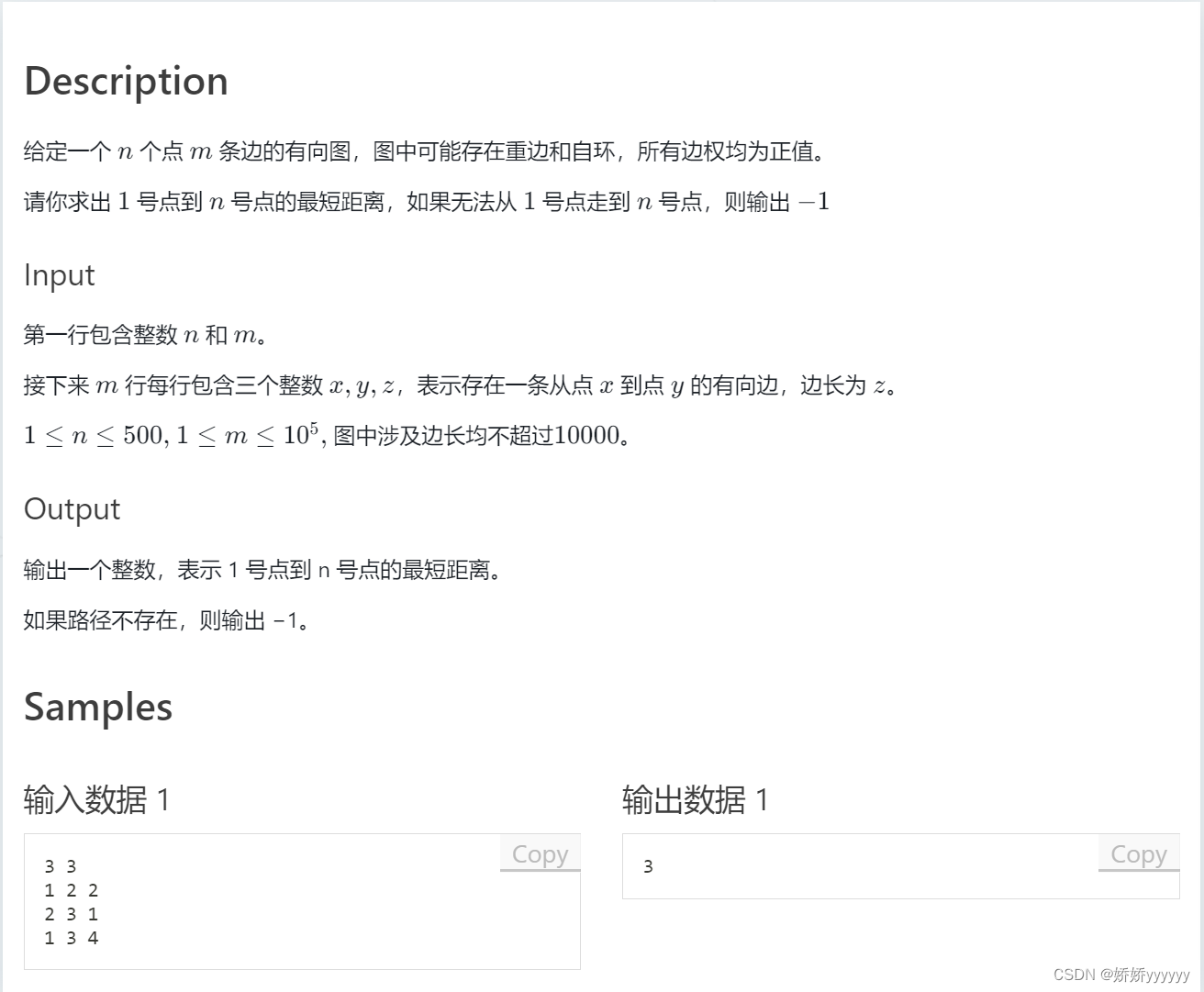
1.朴素Dijkstra:
AC代码:
#include<bits/stdc++.h>using namespace std;const int N = 510;
int g[N][N];
int dis[N];
bool st[N];
int n,m;
int dij()
{memset(dis,0x3f,sizeof dis);dis[1] = 0;for(int i=0;i<n;i++){int t = -1;for(int j=1;j<=n;j++){if(!st[j] && (t==-1 || dis[t]>dis[j]))t=j;}st[t] = true;for(int j=1;j <= n;j++){dis[j] = min(dis[t]+g[t][j],dis[j]);}}if(dis[n] == 0x3f3f3f3f) return -1;return dis[n];
}
int main()
{cin>>n>>m;memset(g,0x3f,sizeof g);while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);g[a][b] = min(g[a][b],c);}int t = dij();cout<<t<<endl;return 0;
}2、堆优化Dijkstra:
AC代码:
#include<bits/stdc++.h>using namespace std;const int N = 15e4+10;
typedef pair<int ,int>PII;
int h[N],e[N],ne[N],idx,w[N];
int n,m;
int dis[N],st[N];
void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}int dij()
{memset(dis,0x3f,sizeof dis);dis[1] = 0;priority_queue<PII,vector<PII>,greater<PII>>heap;heap.push({0,1});//距离加顶点;while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second,distance = t.first;if(st[ver]) continue;st[ver] = true;for(int i=h[ver];i!=-1;i= ne[i]){int j = e[i];//为了更新其他的边if(dis[j] > w[i] + dis[ver] && !st[j]){dis[j] =w[i]+ dis[ver];heap.push({dis[j],j});}}}if(dis[n] == 0x3f3f3f3f ) return -1;return dis[n];
}
int main()
{cin>>n>>m;memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}cout<<dij()<<endl;return 0;
}3、 有边数限制的最短路:
AC代码:
#include<bits/stdc++.h>using namespace std;const int N = 520,M = 10010;
int n,m,k;
int dis[N],backup[M];struct Edge
{int a,b,w;
}edges[M];int bellman_ford()
{memset(dis,0x3f,sizeof dis);dis[1] = 0;for(int i = 0; i < k; i ++){memcpy(backup,dis,sizeof dis);for(int j=0;j< m;j ++){int a = edges[j].a,b=edges[j].b,w=edges[j].w;dis[b] = min(dis[b],backup[a] + w);}}if(dis[n] > 0x3f3f3f3f/2 ) return -1;return dis[n];
}
int main()
{cin>>n>>m>>k;for(int i=0;i<m;i++){int a,b,w;scanf("%d%d%d",&a,&b,&w);edges[i] = {a,b,w};}int t = bellman_ford();if(t == -1) puts("impossible");else printf("%d\n",t);return 0;
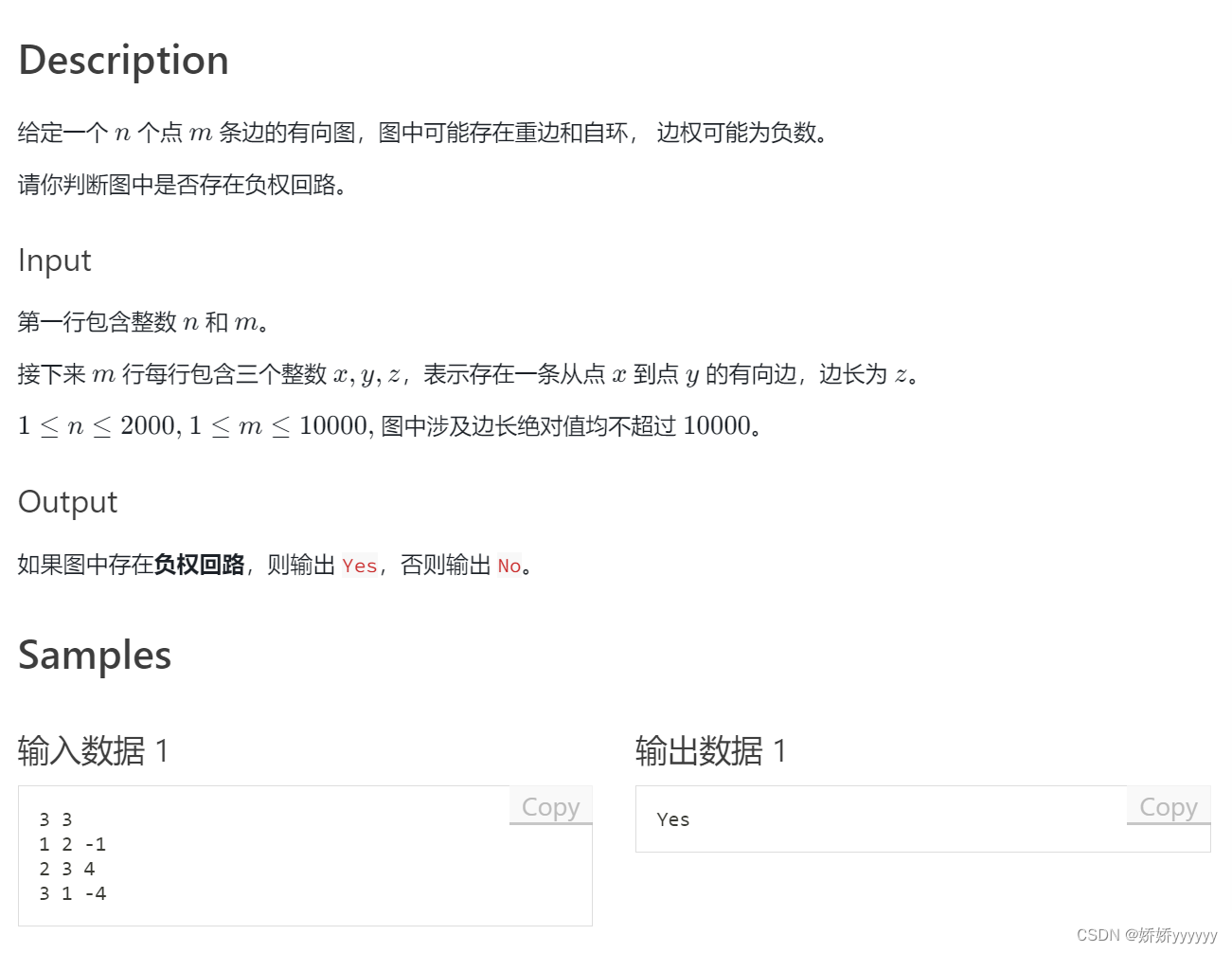
}4、spfa判断负环:
AC代码:
#include<bits/stdc++.h>using namespace std;const int N = 15e4+10;
typedef pair<int ,int>PII;
int h[N],e[N],ne[N],idx,w[N];
int n,m;
int dis[N],st[N],cnt[N];
void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}int spfa()
{dis[1] = 0;queue<int>q;for(int i=1;i<=n;i++){st[i]= true;q.push(i);}while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i=h[t];i!=-1;i = ne[i]){int j= e[i];if(dis[j] > dis[t] + w[i]){dis[j] = dis[t]+w[i];cnt[j] = cnt[t] + 1;if(cnt[j]>=n) return true; q.push(j);st[j] = true;}}}return false;
}
int main()
{cin>>n>>m;memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}if(spfa()) puts("Yes");else puts("No");return 0;
}5、spfa求最短路:
AC代码:
#include<bits/stdc++.h>using namespace std;const int N = 15e4+10;
typedef pair<int ,int>PII;
int h[N],e[N],ne[N],idx,w[N];
int n,m;
int dis[N],st[N];
void add(int a,int b,int c)
{e[idx] = b,w[idx] = c,ne[idx] = h[a],h[a] = idx ++;
}int dij()
{memset(dis,0x3f,sizeof dis);dis[1] = 0;queue<int>q;q.push(1);st[1] = true;while(q.size()){int t = q.front();q.pop();st[t] = false;for(int i=h[t];i!=-1;i = ne[i]){int j= e[i];if(dis[j] > dis[t] + w[i]){dis[j] = dis[t]+w[i];q.push(j);st[j] = true;}}}if(dis[n] == 0x3f3f3f3f) return -1;return dis[n];
}
int main()
{cin>>n>>m;memset(h,-1,sizeof h);while(m--){int a,b,c;cin>>a>>b>>c;add(a,b,c);}int t = dij();if(t == -1) puts("impossible");else cout<<t<<endl;return 0;
}6、Floyd求最短路:
AC代码:
#include<bits/stdc++.h>using namespace std;const int N = 210,INF= 1e9;int n,m,q;
int d[N][N];
int main()
{cin>>n>>m>>q;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i == j) d[i][j] == 0;else d[i][j] = INF;}}while(m--){int a,b,w;scanf("%d%d%d",&a,&b,&w);d[a][b] = min(d[a][b],w);}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j] = min(d[i][j],d[i][k]+d[k][j]);}}}while(q--){int a,b;scanf("%d%d",&a,&b);if(d[a][b]>INF/2) puts("impossible");else printf("%d\n",d[a][b]);}return 0;
}






 (LALA-PG))






)

 —— 任务挂起和恢复)







)