java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：https://blog.csdn.net/grd_java/article/details/123063846

法一：桶排序思想

解题思路

1. 题目说，每个集合的值都是1 ~ n，一般我们会想到将数组中元素，挨个作为key放入map中，然后遍历1~n从map中获取value，看看谁是0，谁是2.
2. 但是我们可以直接再创建一个数组，长度为n+1，用下标来代表数字，将1~n的个数，放入桶中。比如遍历nums数组是，当前元素是1，就放入下标为1的桶中，此时这个桶有1个元素，当我们有遍历到1时，再次放入下标为1的桶，此时这个桶有2个元素。
   

代码:时间复杂度O(n) 空间复杂度O(n)

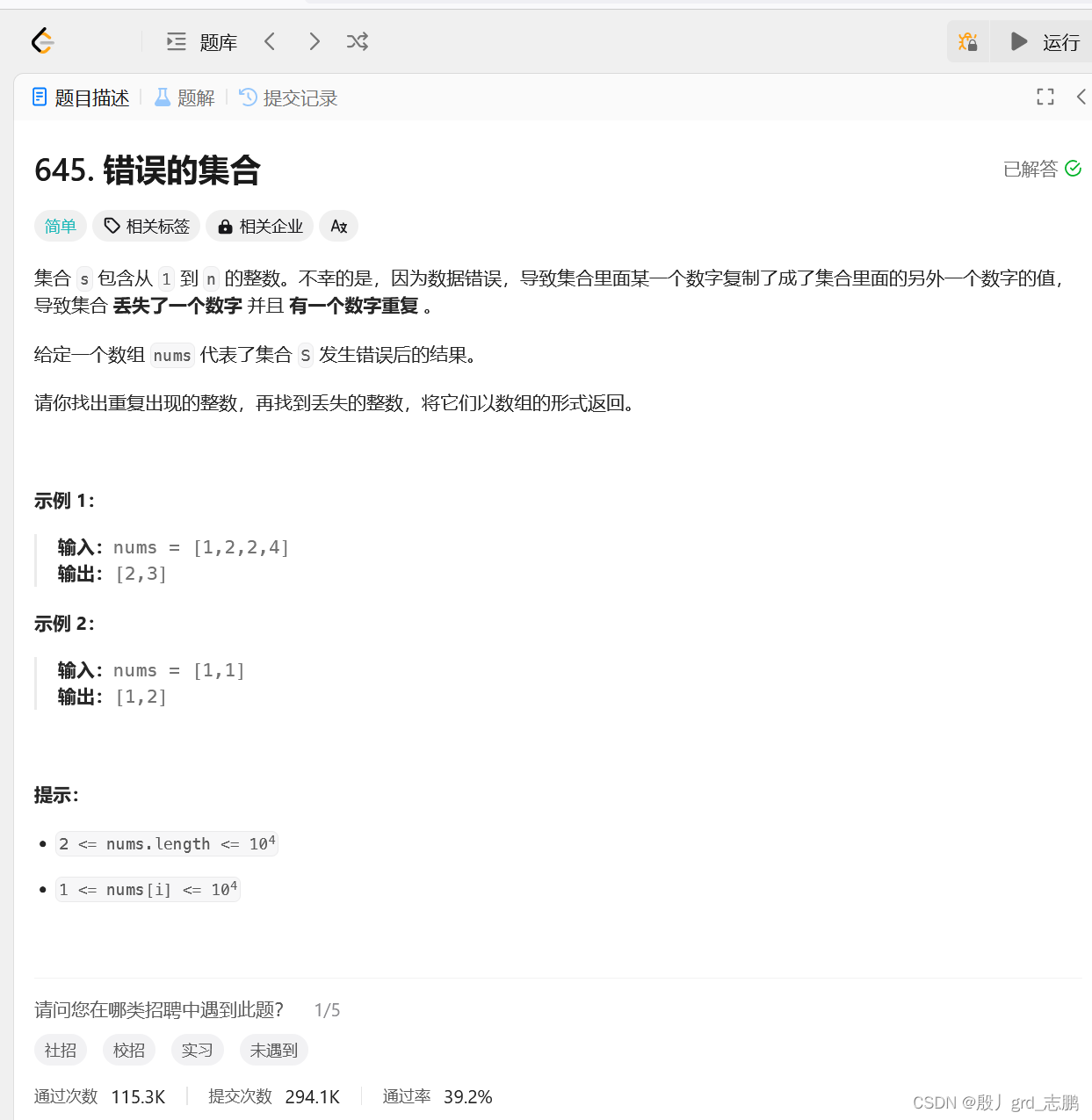
class Solution {public int[] findErrorNums(int[] nums) {int[] ans = new int[2];//答案要求返回形式int[] bucket = new int[nums.length + 1];//桶排序的思想，因为nums中的值固定为1~nfor (int num : nums) bucket[num]++;//将数组中的值，放入对应的桶for (int i = 1; i <= nums.length; i++) {//依次遍历1~nif (bucket[i] == 0) ans[1] = i;//如果当前桶中元素个数为0，说明集合缺少这个元素else if (bucket[i] == 2) ans[0] = i;//如果当前桶有2个元素，说明集合中这个值有重复if (ans[0] != 0 && ans[1] != 0) break;//如果已经找到答案，就无需继续遍历了}return ans;//返回答案}
}

法二：位运算

题目细节

1. 每个集合包含的元素必然为1 ~ n。例如n = 4，那么集合可以是[1,2,3,4],[1,2,4,3],[4,3,2,1]等等，但是必然包含1,2,3,4,也就是1~n这n个数。
2. 但是题目说了，每个集合都发生了错误，有一个数字重复，而另一个数字消失了，比如[1,2,2,4], 正确的应该是包含1,2,3,4这4个数，但是现在少了一个3.

位运算

1. 异或

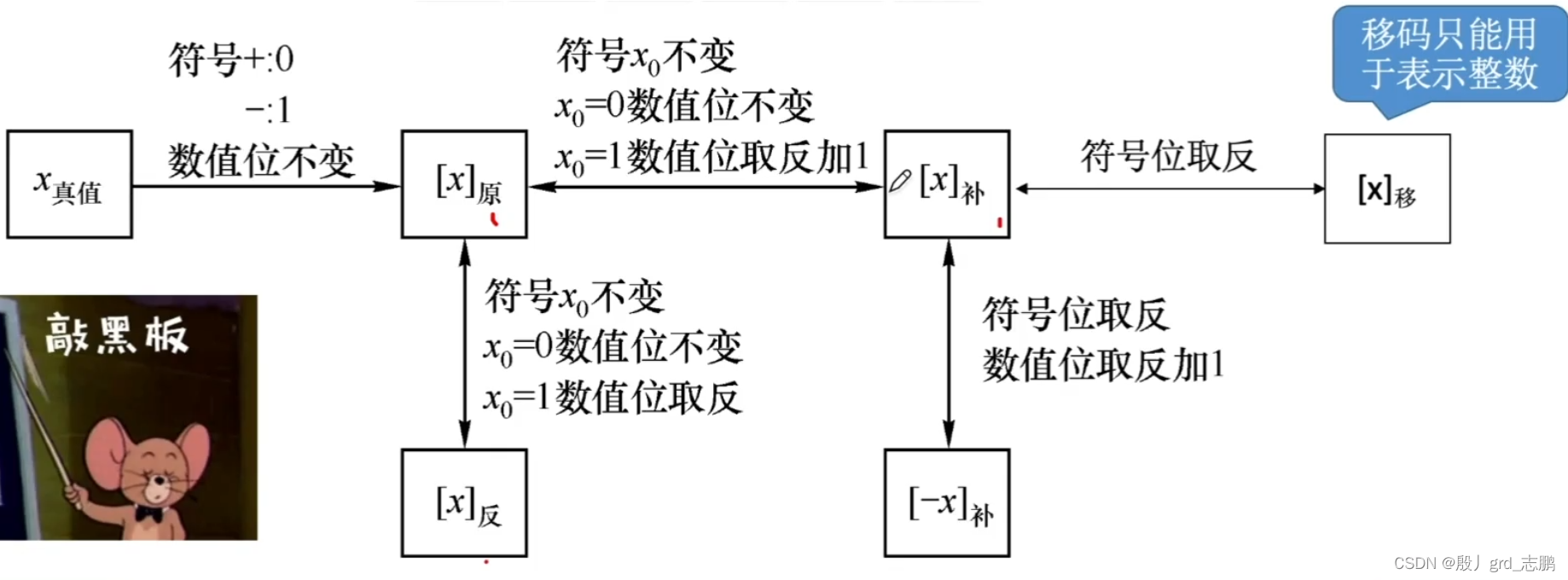
1. 两数相同异或为0，两数不相同异或为1
2. 任何数a异或0，都等于a本身。0 ⊕ a = a
3. 两个相同的数异或必然为0。a ⊕ a = 0;
4. 异或具有结合律和交换律。

1. 结合律0⊕1⊕2⊕2 = (0⊕1)⊕(2⊕2) = 1 ⊕ 0 = 1;
2. 交换律0⊕1⊕2⊕2 = 2⊕1⊕2⊕0

2. 与

1. 两个数都是1，相与为1. 1&1=1
2. 两个数有一个是0，相与为0,1&0=0

3. 补码

1. C，C++，java等编程语言中，为了更好的和硬件交互，数字以补码形式存储。
2. 各种码的转换关系如下，了解即可，我们只需要统一用补码进行计算即可。（看不懂没关系，继续看下面）
   
   

补码（了解即可）

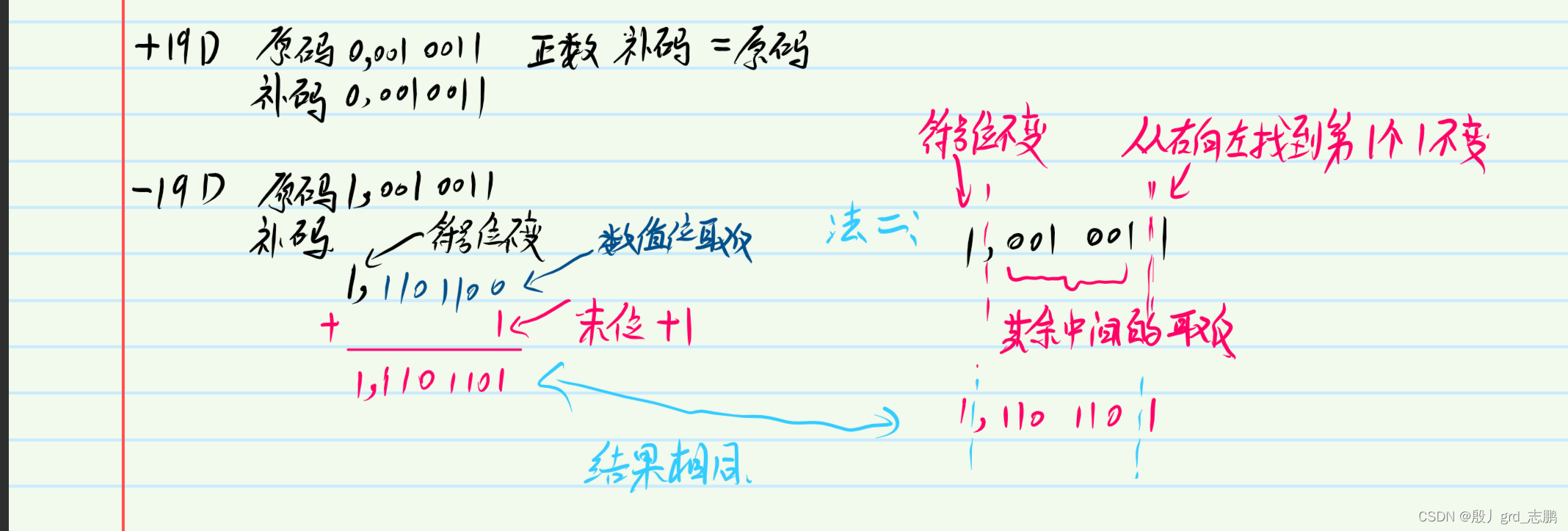
1. 真值：我们通过除基取余法得到的二进制代码，统一称为真值。例如十进制数8的二进制位1000，这个1000就是一个真值。
2. 原码：那么如何区分真值是正数还是负数呢？我们只需要用掉开头的一个二进制位，0表示正数，1表示负数。例如8的原码就是0000 … 1000 标红的那位就是符号为，剩下的都是数值位. -8的原码就是1000 … 1000负数的符号位为1.
3. 补码，方便计算机运算的一种码，它不方便人类理解，但是方便计算机。它可以通过原码来推导

1. 正数的补码 = 原码
2. 负数的补码 = 符号位不变，其余位取反，然后末位+1。当然我们有一个口诀，就是从右向左找到第一个1，然后将符号位和这个1之间所有元素按位取反即可（图解如下）
   

这道题，需要你知道关于补码的什么呢？

1. 集合中保存的都是1~n的正数，计算机保存也都是补码，也就是符号位为0表示正数
2. 正数的补码和源码是一样的，例如1 = 0,000 0000 0000 0000 0000 0000 0000 0001 （以32位进行保存）
3. 负数的补码和源码的区别是，符号位和最右边的1不变，这两个不变的二进制位中间的其余数值位全部取反

1. 原码：例如-1= 1,000 0000 0000 0000 0000 0000 0000 0001
2. 补码：例如-1= 1,111 1111 1111 1111 1111 1111 1111 1111

4. 我们现在有了1和-1的补码。

1. 1 = 0,000 0000 0000 0000 0000 0000 0000 0001
2. -1= 1,111 1111 1111 1111 1111 1111 1111 1111
3. 我们发现，除了最右边的1以外，这个1左边所有的数，都是不同的。

5. 如果此时我执行1与-1 也就是 1 & （-1）

我会得到0,000 0000 0000 0000 0000 0000 0000 0001，也就是除了最右边的1以外，其余全是0. 这样我就得到了这个数的最低位的那个1.也就是我得到了这个数，最右边的一个二进制1的位置。并且其余二进制位全是0

6. 得到它有什么用呢？作用就是简化判断条件，让我们只需要用if考虑两种情况，而不是无数种。

1. 0 & 任何数都是0，只有1 & 1 才能唯一的 = 1. 这就是它的作用。对于最终得到的只有最右1，其余全为0的二进制串lowbit = 0,000 0000 0000 0000 0000 0000 0000 0001来说，只有遇到一个同样1在最右边的数才会不为0，否则它必然为0.
2. 它让任何数与其相与只有两种结果，要么为1，要么为0.而不是各种值。

1. 例如 8 = 0,000 0000 0000 0000 0000 0000 0000 1000
2. 和lowbit相与0,000 0000 0000 0000 0000 0000 0000 0001
3. 结果为==0,000 0000 0000 0000 0000 0000 0000 0000

3. 如果不进行只取最右边1的操作，直接随便两个数呢？

8的二进制补码为：0000 … 1000
9的二进制补码为：0000 … 1001
异或结果为：==== 0000 … 1000 这个值=8，不同的数，还有无穷多种结果
请你告诉我，我该如何写if语句，描述这大量的结果呢？我们当然希望只有0或者1两种状态，以方便我们写if语句。所以这就是只保留最右边的1，其余全部为0的作用。

解题思路

1. 案例的补码

1. 1的补码:0,000 0000 0000 0000 0000 0000 0000 0001
2. 2的补码:0,000 0000 0000 0000 0000 0000 0000 0010
3. 3的补码:0,000 0000 0000 0000 0000 0000 0000 0011
4. 4的补码:0,000 0000 0000 0000 0000 0000 0000 0100

2. 找到，缺少的数和重复的数的异或结果，记为xor。

1. 整体异或消除重复的元素：1⊕2⊕2⊕4 = 1⊕0⊕4 = 1⊕4. 这里利用了异或的结合律和异或规律（相同的数异或 = 0）
2. 和1~n异或获得重复的数和缺少的数的异或。1⊕4⊕1⊕2⊕3⊕4 = (1⊕1)⊕(4⊕4)⊕(2⊕3) = 2⊕3此时就是重复的数2，和缺少的数3的异或结果。记为xor

3. 找到xor这个异或结果的最低位1. 上面说过，这个操作就是将if判断简化为只需要判断是0还是1，而不是无穷多种.

xor & (-xor) = 只保留最低位的1，其余全为0. 记为lowbit = 0,000 0000 0000 0000 0000 0000 0000 0001。这里很巧，这个例子的lowbit正好是1的补码。

4. 这道题需要两个结果，一个是缺少的数,另一个是重复的数

我们这里常用的套路就是分成两组计算。因为我们上面分析过，任何数和lowbit相与，只有0和1两种结果。我们将与lowbit相与为0分为一组，让它和num1进行异或。与lowbit相与为1的分为另一组，让它和num2进行异或。

5. nums数组中的值[1,2,2,4]，依次和lowbit进行分组异或. 可以获得两个没有任何问题的数。也就是既不是丢失的，也不是重复的。

1. 1&lowbit = 1, num2 ^=1 = 0⊕1=1. 首先是1这个数，与lowbit相与，发现值为1，将其分为1组，和num2进行异或
2. 2&lowbit = 0, num1 ^=2 = 0⊕2=2. 然后2这个数，与lowbit相与，发现值为0，分到0组，和num1异或
3. 2&lowbit = 0, num1 ^=2 = 2⊕2 = 0. 然后又是2这个数，与lowbit相与，发现值为0，0组异或
4. 4&lowbit = 0, num1 ^=4 = 0⊕4 = 4. 最后是4这个数，与lowbit相与，发现值为0，0组异或
5. 最终，num1 = 4，num2 = 1

6. 然后和1~n，也就是1,2,3,4进行再次分组异或，找到两个有问题的数。也就是重复的，和丢失的

1. 1&lowbit = 1, num2 ^=1 = 1⊕1 = 0.
2. 2&lowbit = 0, num1 ^=2 = 4⊕2 = 6. 这个6是二进制转换过来的，大家可以自己用代码算
3. 3&lowbit = 1, num2 ^=3 = 0⊕3 = 3.
4. 4&lowbit = 0, num1 ^=4 = 6⊕4 = 2.
5. 最终，num1 = 2，num2 = 3。但是到底谁是丢失的，谁是重复的，我们也不知道

7. 再次进行nums数组[1,2,2,4]的遍历比对，看看num1是否保存的是重复的值，如果是，num1作为重复值，num2作为缺失值返回。否则num1作为缺失值，num2作为重复值返回

代码:时间复杂度O(n) 空间复杂度O(1)

class Solution {public int[] findErrorNums(int[] nums) {//异或 两个数相同异或为0，两个数不同异或为1//任何数a异或0，都等于a本身。0 ⊕ a = a //两个相同的数异或必然为0。a ⊕ a = 0;//最关键的是，异或具有结合律。0⊕1⊕2⊕2 = (0⊕1)⊕(2⊕2) = 1 ⊕ 0 = 1; int n = nums.length;int xor = 0;//整体异或消除重复的元素：1⊕2⊕2⊕4 = 1⊕0⊕4 = 1⊕4. 这里利用了异或的结合律和异或规律（相同的数异或 = 0）for(int num:nums) xor ^= num;//和1~n异或获得重复的数和缺少的数的异或。1⊕4⊕1⊕2⊕3⊕4 = (1⊕1)⊕(4⊕4)⊕(2⊕3) = 2⊕3此时就是重复的数2，和缺少的数3的异或结果。记为xorfor(int i = 1;i<=n;i++) xor^=i;//xor & (-xor) = 只保留最低位的1，其余全为0. 记为lowbit = `0`,000 0000 0000 0000 0000 0000 0000 0001。这里很巧，这个例子的lowbit正好是1的补码。int lowbit = xor & (-xor);//用两个变量，分别记录这道题答案需要的两个值int num1 = 0, num2 = 0;//初始为0//我们这里常用的套路就是分成两组计算。因为我们上面分析过，任何数和lowbit相与，只有0和1两种结果for(int num:nums){//nums数组中的值[1,2,2,4]，依次和lowbit进行分组异或. 可以获得两个没有任何问题的数。也就是既不是丢失的，也不是重复的。if((num & lowbit)==0) num1^=num;else num2 ^= num;}//然后和1~n，也就是1,2,3,4进行再次分组异或，找到两个有问题的数。也就是重复的，和丢失的for(int i = 1;i<=n;i++){if((i & lowbit)==0) num1^=i;else num2^=i;}//再次进行nums数组[1,2,2,4]的遍历比对，看看num1是否保存的是重复的值，如果是，num1作为重复值，num2作为缺失值返回。for(int num:nums){if(num==num1) return new int[]{num1,num2};}//否则num1作为缺失值，num2作为重复值返回return new int[]{num2,num1};}
}