多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
方法一:哈希表
class Solution {public int majorityElement(int[] nums) {HashMap<Integer, Integer> map = new HashMap<>();for (int num : nums) {if (map.containsKey(num)) {map.put(num, map.get(num) + 1);} else {map.put(num, 1);}}int max = 0;int res = 0;for (Map.Entry<Integer, Integer> integerIntegerEntry : map.entrySet()) {if (integerIntegerEntry.getValue() > max) {max = integerIntegerEntry.getValue();res = integerIntegerEntry.getKey();}}return res;}
}
方法二:排序
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 n/2 的元素(下标从 0 开始)一定是众数。
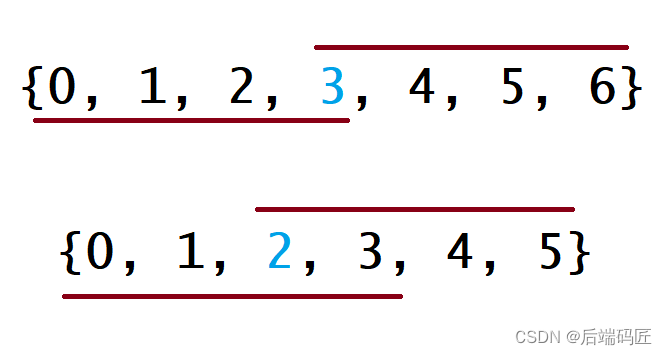
class Solution {public int majorityElement(int[] nums) {Arrays.sort(nums);return nums[nums.length / 2];}
}
方法三:随机化
这个思路很独特,感觉看脸。
因为超过 n/2 的数组下标被众数占据了,这样我们随机挑选一个下标对应的元素并验证,有很大的概率能找到众数。
class Solution {private int randRange(Random rand, int min, int max) {return rand.nextInt(max - min) + min;}private int countOccurences(int[] nums, int num) {int count = 0;for (int i = 0; i < nums.length; i++) {if (nums[i] == num) {count++;}}return count;}public int majorityElement(int[] nums) {Random rand = new Random();int majorityCount = nums.length / 2;while (true) {int candidate = nums[randRange(rand, 0, nums.length)];if (countOccurences(nums, candidate) > majorityCount) {return candidate;}}}
}


-《udp发送信息》)



:670. 最大交换)




)
详解)
)




)
