一、说明

   极点和极线（Pole and polar）对于几何学，是普遍的概念。可能高中就学过，问题是在双曲几何又用到这个概念。前面已经有写过一文，经过再次学习，逐渐感觉前文描述不很理想，这一文专门纠正前文的不足点。
前文地址是：【双曲几何学 02】什么是极点和极线？
参考文：【射影几何09】交比定律和迪萨格定律

二、基本概念

   【 在几何学中，极点和极线分别是相对于给定圆锥截面具有唯一倒数关系的点和线】。这话听起来很吃力，那么，我们从圆开始一点点理解吧。

2.1 圆的极点和极线

2.2.1 圆外极点

   给定圆O，和圆外一个点P，从P做圆O的切线，此种切线能做出两条，它们分别分别与圆O相切于M、N两个点，此时，P是相对于圆O的极点（pole）而MN是伴随极点P的极线。
  显然，$OP\perp MN$,因此，$P$和$MN$是一个对偶。记为$P^{\perp }=MN$或反之$M{N}^{\perp }=P$

2.1.2 特殊位置极点

   下面尝试两个特殊位置的极点和极线。
   1）极点P恰好落在圆上：
   2）极点P落在圆内部：

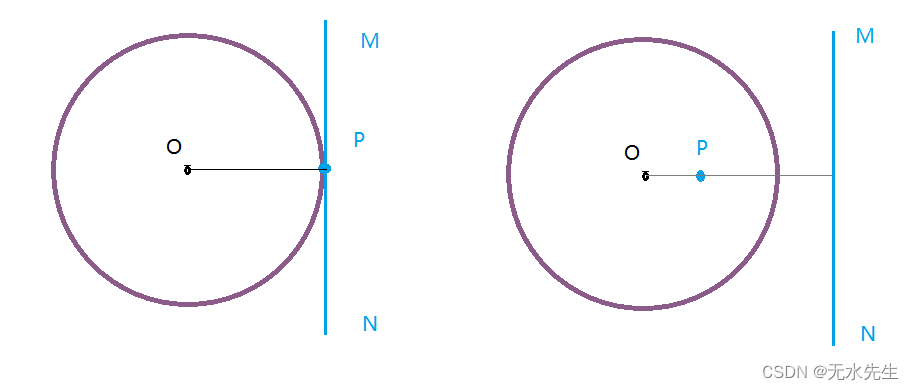
   以上两种情况如何确定极线？我们下一章将继续探讨。

2.2 圆锥曲线的极点

   在其它的圆锥曲线上，极点和极线定义完全雷同，事实上，因为椭圆、双曲都是圆在另一个平面的投影，因此，不必关注其它圆锥线，只要在圆上讨论其中性质，然后做一个投影，就能将原理和结论翻转到对应圆锥曲线中。

   然而，上图显出，在圆上的属性，有些无法和椭圆上一致，比如，在圆上MN和OP垂直，在椭圆上未必；在圆和椭圆上，有什么极点和极线的属性使得在圆和椭圆上均能成立呢？让我们继续下文的讨论。

三、极点的属性

3.1 调和点列

   不在圆上的一点P，作直线l交圆于M、N两点，则在L上有且只有一点Q，使得交比(MN，QP)=-1（即M、N、Q、P 构成一调和点列）。当改变L的倾角，绕着P旋转发出直线和RS相交Q时，Q点与其它三点构成调和序列，RS即P的极线。或者表述成：Q点要想构成调和，其轨迹必须在RS上。

3.2 调和点列和交比点列的关系

   首先说，调和点列就是一个交比点列。为了清除表达和便以记忆，我们这里专门给出一段陈述。
1）交比点列
一般地，将交比点列（A，B；C，D）中，AB定义成基点，CD定义成分点，那么交比是：
$$\lambda 1=\frac{AC}{CB}$$
$$\lambda 2=\frac{AD}{DB}$$
$$（A，B；C，D）=\frac{\lambda 1}{\lambda 2}$$
对应图为：

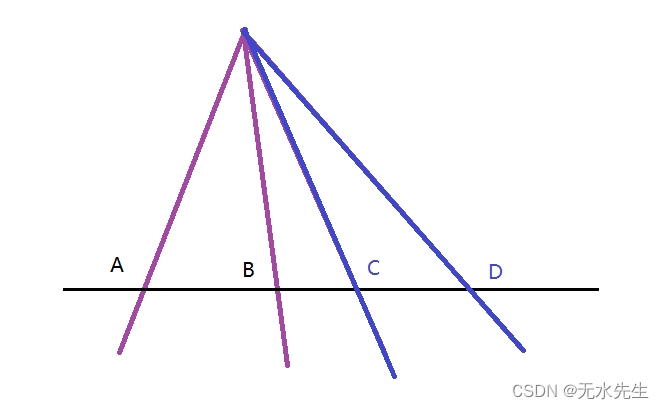
   这里显然，CD作为两个分点，都在基点AB的外侧。
   如果出现下列情况，分点C在AB内测，而D在AB外测，于是：

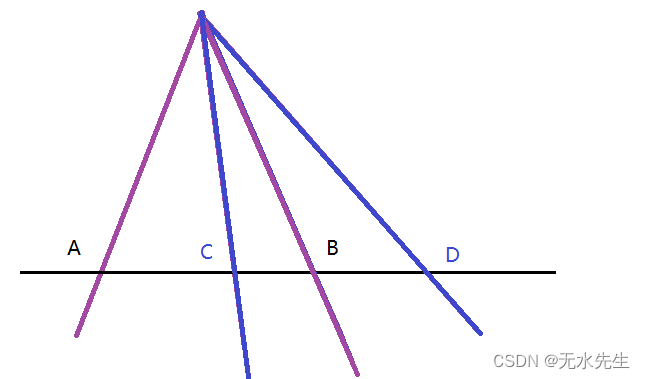
那么交比是：
$$\lambda 1=\frac{AC}{CB}$$
$$\lambda 2=\frac{AD}{DB}$$
$$（A，B；C，D）=\frac{\lambda 1}{\lambda 2}=-1$$
   那么，（A，B；C，D）就构成调和点列。

3.3 通过作图找到极线

   以上叙事中，我们在头脑里很容易构建P极点和极线的概念，然而，在作图中，无法清晰构建极线，因为极线的切点无法清楚给出。下文中，我们将清楚告诉大家，对于任意极点，极线如何找出。（这里我们先不引出证明，证明部分在后文给出）

如上图，从极点P，向圆O发出两条射线，交圆于【α，β】点，和【γ，Π】点，使得【α，β，Π，γ】构成四边形，延长四边形的边【α，γ】和【β，Π】它们交于S点；做四边形对角线【α， Π 】和【 β， γ】交于R点，那么，R和S的连线，就和P的极线MN重合。

• 注意：我们这里陈述一个做图事实，并不去证明其合理性。
• P发出的射线与该射线角度无关，只要能与圆相交就可以。

3.3 极点在圆内，如何找到极线？

   如果P是极点，并且在圆内，如何按照上文方法找出P对应极线？
首先，过P做圆O的两条弦【α，γ】和【 β，Π 】此四点构成圆O内接四边形。分别延长线段【α，β】和线段【γ，Π】交于N，同理延长【α， Π 】和【 β， γ】交于M，此M和N的连线就是P点的极线。

四、后记

   该文只是解释了相关知识和概念，对于证明，我们将在后续系列文章中给出。