
文章目录
- 经典格言
- 数学习题
- 古今评注
- 拓展学习
- (一)大数定理
- (二)伯努利级数
经典格言
真正的问题,不在于机器是否思考,而在于人们是否思考。——B·F·斯金纳(B. F. Skinner)
B·F·斯金纳,这位行为主义心理学的大师级人物,以一句振聋发聩的名言揭示了一个引人深思的观点:“真正的问题,不在于机器是否思考,而在于人们是否思考。”这句话犹如一把锐利的双刃剑,一方面切割了对于人工智能过度关注其是否具备“思考”能力的传统迷思,另一方面则尖锐地指向了人类自身在信息爆炸时代所面临的认知挑战。
首先,斯金纳的这番言论对科技发展的反思可谓一针见血。随着人工智能和机器学习技术的日新月异,社会上关于“机器是否会思考”的讨论热度始终居高不下。然而,在斯金纳看来,这种担忧或许偏离了重点。毕竟,机器思考与否并不直接影响到我们作为人类的生活质量和思维深度,无论机器多么智能,它依然是由人类设计并服务于人类需求的工具。与其纠结于机器能否模拟人类思考,不如聚焦于如何利用这些技术更好地提升人类生活和促进社会发展。
其次,这句话更是对我们自身的一种警醒。在信息过载的时代背景下,便捷的搜索、海量的数据、高效的算法似乎正逐步替代人们的深度思考与独立判断。人们越来越依赖于机器处理信息、解决问题,而在这一过程中,个体主动思考的习惯和能力却可能在悄然退化。斯金纳提醒我们,真正的危机并非来自机器可能拥有的思考能力,而是人类自身在知识获取过程中逐渐丧失的批判性思考、创新思维以及道德判断等核心素养。
因此,斯金纳的这句名言既是对科技进步的独特洞察,又是对人类内在精神世界的深刻关切。他倡导我们在拥抱智能化的同时,更应坚守思考的价值,保持对世界的好奇心与独立见解,使科技发展真正成为推动人类进步而非取代人类智慧的力量源泉。
数学习题
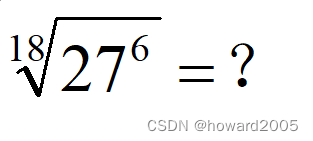
古今评注
伯努利家族,这个听起来像是马戏团里高超杂技世家的名字,实际上是一个星光熠熠的数学家集群。在17世纪至18世纪的欧洲科学界,他们就像是一串璀璨的数学明珠,镶嵌在了历史的长河中,以其独特的家族竞争和卓越贡献,在数学乃至物理学领域留下了深刻的印记。
首先出场的是家族中的两位先驱者——雅各布·伯努利(Jacob Bernoulli,1654-1705)与约翰·伯努利(Johann Bernoulli,1677-1748),兄弟俩虽同出一门,却在数学战场上犹如一对激烈的竞争对手。他们在微积分学、概率论等领域你追我赶,共同推动了数学的进步。雅各布是“大数定律”的发现者,而约翰则在教学和科研上独树一帜,他们的学术之争犹如一场没有硝烟的智慧之战,为后世留下了丰富的数学遗产。
随后,约翰的两个儿子尼古拉·伯努利(Nicholas Bernoulli,1695-1726)和丹尼尔·伯努利(Daniel Bernoulli,1700-1782)继承了家族的数学基因。然而,命运似乎给尼古拉开了一个残酷的玩笑,他在年仅31岁时因一次不幸的溺水事故英年早逝,其数学才华如同流星划过夜空,短暂却耀眼。但他的探索精神无疑为家族荣耀增添了一抹悲壮色彩。
相比之下,丹尼尔·伯努利则像一颗持久燃烧的恒星,他不仅在数学领域成就斐然,提出了著名的“伯努利定律”对流体力学做出了重大贡献,还涉足统计力学、概率论等多个科学领域。他的智慧之光一直照亮到82岁的高龄,直至生命尽头,都在孜孜不倦地探索科学的边界。
总之,伯努利家族堪称数学界的“梦幻队”,他们之间的竞争与合作,既有家族亲情的温馨互动,又有学术争鸣的激烈碰撞,这种独特的家族氛围和不懈追求科学真理的精神,使得他们在世界数学史上留下了浓墨重彩的一笔。
拓展学习
(一)大数定理
大数定理是概率论中的核心理论之一,主要描述了在重复独立随机试验中,随着试验次数趋于无穷大时,事件发生的频率趋于其概率的规律。这个定理包含两种表述形式:
-
弱大数定律(Weak Law of Large Numbers, WLLN):如果有一个独立同分布的随机变量序列 { X 1 , X 2 , . . . , X n } \{X_1, X_2, ..., X_n\} {X1,X2,...,Xn},且它们的期望值都为同一个常数 μ \mu μ,那么当样本容量 n n n 趋向于无穷大时,样本均值 ( 1 n ) ⋅ ( X 1 + X 2 + . . . + X n ) \displaystyle\left(\frac{1}{n}\right) \cdot (X_1 + X_2 + ... + X_n) (n1)⋅(X1+X2+...+Xn) 几乎必然地(以概率1的方式)趋近于 μ \mu μ。这意味着对于任何正数 ε \varepsilon ε,样本均值与期望值之差的绝对值大于 ε \varepsilon ε 的概率将随着试验次数增加而趋于零:
lim n → ∞ P ( ∣ 1 n ( X 1 + X 2 + ⋯ + X n ) − μ ∣ > ε ) = 0 \lim_{n \to \infty} P\left(\left|\frac{1}{n}(X_1 + X_2 + \cdots + X_n) - \mu\right| > \varepsilon\right) = 0 n→∞limP(∣∣∣∣n1(X1+X2+⋯+Xn)−μ∣∣∣∣>ε)=0 -
强大数定律(Strong Law of Large Numbers, SLLN):强大数定律比弱大数定律更强硬,它表明上述随机变量序列的样本均值以几乎处处收敛(即概率1的方式)到期望值 μ \mu μ:
P ( lim n → ∞ 1 n ( X 1 + X 2 + ⋯ + X n ) = μ ) = 1 P\left(\lim_{n \to \infty} \frac{1}{n}(X_1 + X_2 + \cdots + X_n) = \mu\right) = 1 P(n→∞limn1(X1+X2+⋯+Xn)=μ)=1
这意味着除了一个概率为零的集合外,样本均值对所有的实验结果都将无限接近于 μ \mu μ。
简单来说,大数定理告诉我们,在进行大量独立重复试验时,尽管每次试验的结果可能有波动,但长期来看,试验结果的平均值会非常稳定地接近某个确定值(即该事件的概率或期望值)。这一理论在统计推断、保险精算、风险评估等领域具有极其重要的应用价值。
(二)伯努利级数
伯努利级数(Bernoulli series)是数学分析中的一个概念,它是以瑞士数学家雅各布·伯努利命名的一类幂级数。在微积分学中,伯努利多项式是一组特殊的多项式序列,每一项伯努利多项式的系数都是伯努利数。
伯努利多项式通常表示为 B n ( x ) B_n(x) Bn(x),其中 n n n 为非负整数, x x x 是一个变量。伯努利多项式的递推公式定义如下:
- B 0 ( x ) = 1 B_0(x) = 1 B0(x)=1
- B 1 ( x ) = x − 1 2 B_1(x) = x - \frac{1}{2} B1(x)=x−21
- 对于 n ≥ 1 n \geq 1 n≥1,有 B n + 1 ( x ) = ( 2 n + 1 ) x ⋅ B n ( x ) − n ⋅ B n − 1 ( x ) B_{n+1}(x) = (2n + 1)x \cdot B_n(x) - n \cdot B_{n-1}(x) Bn+1(x)=(2n+1)x⋅Bn(x)−n⋅Bn−1(x)
相应的,伯努利级数指的是伯努利多项式关于 x x x 的泰勒级数展开,即 f ( x ) = ∑ n = 0 ∞ B n ( x ) n ! f(x) =\displaystyle \sum_{n=0}^{\infty} \frac{B_n(x)}{n!} f(x)=n=0∑∞n!Bn(x)
其中,伯努利数 B n B_n Bn 是常数项,对于不同的 n n n 值有不同的数值,并且具有丰富的数学特性与应用,例如在解决物理问题、计算特殊函数以及在组合数学等领域都有重要应用。
需要注意的是,这里的“伯努利级数”有时也特指伯努利数生成函数的级数形式,即 ∑ n = 0 ∞ B n n ! x n \displaystyle\sum_{n=0}^{\infty} \frac{B_n}{n!} x^n n=0∑∞n!Bnxn
这个级数可以用来计算任意阶数的伯努利数。






![[java基础揉碎]基本数据类型转换](http://pic.xiahunao.cn/[java基础揉碎]基本数据类型转换)




)



项目实战)


)
