目录
前言:EXCEL里的的向量相关计算公式
0.1 EXCEL里相关公式
0.2 先说结论:向量组的点乘公式和 向量组的点乘公式不一样
1 向量的点乘 (内积)
1.1 向量的点乘公式
1.2 EXCEL里向量点乘的计算
编辑
1.3 向量点乘的性质
1.3.1 内积的公式A*B=|A|*|B|*cos(θ)
1.3.1.2 cos曲线
1.3.2 内积的最大最小值
1.3.3 内积为正负的判断和应用---可用在机器学习上
1.3.4 内积的公式可以理解为
1.4 向量点乘=0时
2 向量组/矩阵的点乘
2.1 向量组/矩阵的点乘
2.2 EXCEL里向量组的乘法
2.3 公式
2.4 图
1 乘法
1.1 标量乘法
1.1.1 乘法的定义
- 乘法的定义
- a*b= a个b之和
- a*b= a 的 b 倍
- 2*3=3+3=6
1.1.2 乘法符合的规律
- 交换律 :a*b= b*a
- 分配律:c*(a+b) =c*a+c*b
- 结合律:c*(a*b)= (c*a)*b
1.2 向量乘法,种类很多
向量:有方向和大小的对象
- 向量只有方向和大小
- 没有具体的位置
向量的乘法:
- 向量的数乘,λ*A
- 向量的数量积,内积,inner product ,N维空间中a*b=a1b1+a2b2+.....an*bn
- 两个向量的分量相乘然后相加求和
- 标准内积,欧几里得内积
- 点积, dot product ,数量积,内积,二维空间中,a*b=|a||b|*cosθ
- 两个向量的分量相乘然后相加求和
- 外积, outer product
- 叉积,cross product ,×乘,叉乘 反交换律,负交换律
2 概念和公式
2.1 向量的数乘
- 向量的数乘,λ*A
2.2 向量的内积 Inner product
内积和点积都是衡量向量相似度的指标
- In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more).
- 也就是说在欧氏空间内向量点积用的很多,也被广泛称为了内积,但是点积的方法并不是唯一被定义的内积方式,点积只是内积其中一种定义方式,用的最多。所以在很多地方,点积和内积被画了等号。关于内积的更多解释可以参见Inner product space。
- 交换律 :a*b= b*a
- 分配律:k*(a+b) =k*a+k*b
- 结合律:c*(a*b)= (c*a)*b
- 对称性:a*b= b*a
- 正定性:对于任何非零向量a, a*a>0
内积公式,计算模长 |a|= 根号(a*a)
距离, distance(a,b)= 根号(a-b)*(a-b)
正交性:点积=0,两个向量垂直正交
2.3 向量的点乘 Dot product,向量点积
- 向量的点积是向量内积特例?
- 符号为
- 要求向量长度相同,结果是一个标量。又称:点乘、数量积、标量积、scalar product、projection product等。
- 交换律 :a*b= b*a
- 分配律:k*(a+b) =k*a+k*b
- 结合律:c*(a*b)= (c*a)*b
- 任何向量*0向量=0向量
- 方向性,0-90度,正,90-180为负数,180-270 点积<0 270-360 >0
- 90 点积=0,向量垂直正交
夹角 :两个向量的夹角,判断向量之间的方向的相似性
投影:1个向量在另外一个向量方向上的投影,再计算
正交性:点积=0,两个向量垂直正交
2.4 向量的外积 Outer product
向量外积,Outer product
- 符号为
- 如果向量 的长度为 ,向量的长度为
- 外积结果是一个矩阵,其维度为
- 过程等价于矩阵的Standard matrix multiplication。
2.5 Cross product[3],向量叉积
- 向量的叉积是向量外积特例?
- 符号为
- 叉积运算只定义在三维空间,结果仍然是一个向量
- 其方向遵循右手定则。又称:叉乘、向量积、vector product等。
另外一种分类方法
2.6 克罗内克积, Kronecker product (外积,叉积都是属于?)
Kronecker product[6],克罗内克积
- Outer product的推广?
- 符号为
- 是上面的向量外积(out product)的推广,形成的是分块矩阵(block matrix),对矩阵维度没有要求。又称:matrix direct product等。
2.7 矩阵乘积 Standard matrix multiplication,最一般的矩阵间乘法。
- 符号为
- 要求 的列数要与 的行数相等,是最一般的矩阵间乘法。
2.8 Hadamard product,哈达玛积(点积就是?)
- 或 符号为
- 或 矩阵对应元素相乘,要求矩阵维度相同。
- 又称:逐元素积、element-wise product、entrywise product、Schur product等。
3 EXCEL里的的向量相关计算公式
3.1 EXCEL里相关公式
- 向量组相乘 : mmult()
- 向量组转置 : transpose()
- 向量组取逆 : minverse()
- 行列数公式
'
python里 numpy的计算
- np.dot()
- np.cross()
3.2 向量组的点乘公式和 向量组的点乘公式不一样
- 向量的点乘 (内积), 可以用sumproduct(),也可以用mmult()
- 向量组的点乘 (内积),尽量用sumproduct(),也可以用 sum( mmult() ),但不能直接用 mmult()
下面是具体的计算
4 向量的内积
定义
作用和应用
几何意义
物理意义
内积的EXCEL计算
内积的VBA计算
内积的python计算
5 向量的点乘 (点积)
4.1 向量的点乘公式
- 向量,这里是至一维向量
- 两个向量的点乘=行向量*列向量 = 常数/标量
- 内积=常数/标量
1.2 EXCEL里向量点乘的计算
- 两个向量的内积=行向量*列向量
- 如果行列向量,设置不对,计算时记得用 transpose()
- 所有矩阵的相乘都可以用muult()
- 但计算内积要注意有时候,只能用sumproduct()
1.3 向量点乘的性质
1.3.1 内积的公式A*B=|A|*|B|*cos(θ)
- 向量的内积=W*X=WT*X=|W|*|X|*cos(θ)
1.3.2 EXCEL里cos(θ) 的计算
- EXCEL里cos(θ) ,其中θ 必须是弧度
- 弧度=角度*PI()/180
- 弧度=RADIANS(角度)
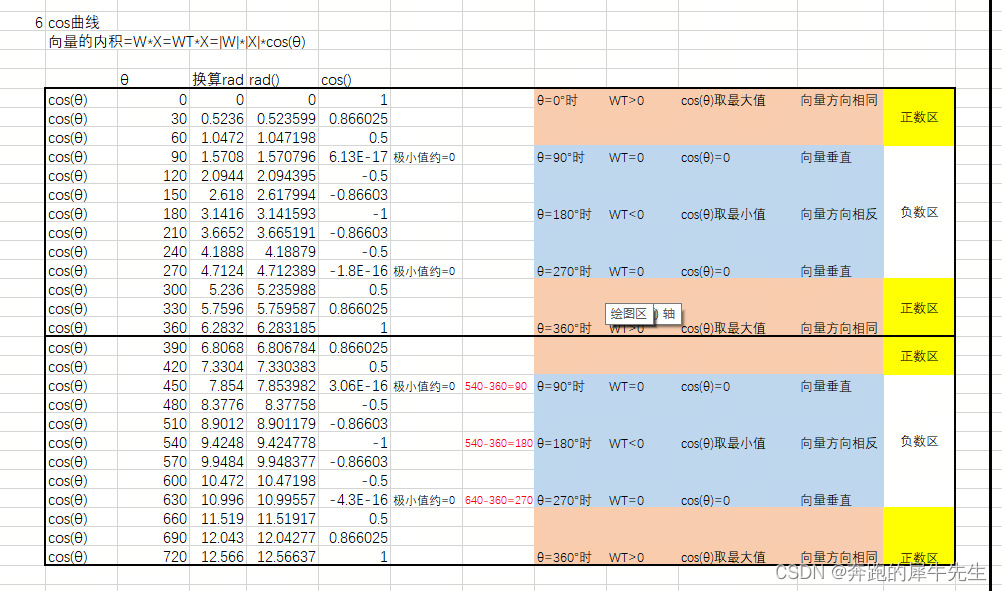
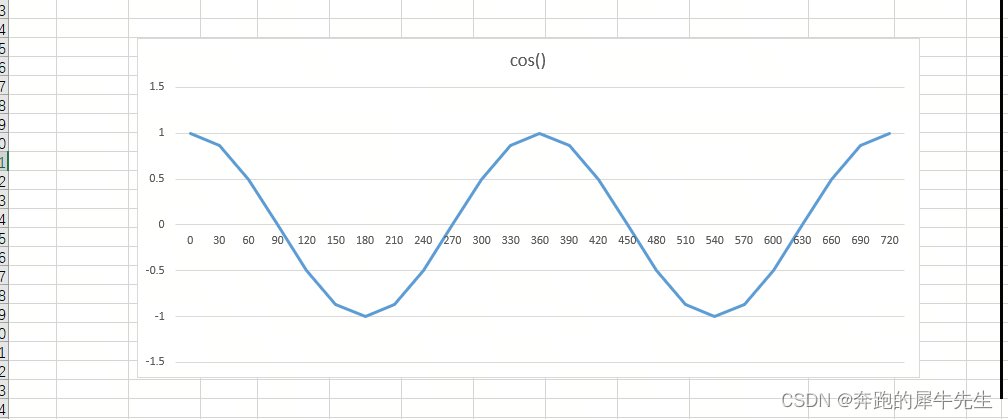
1.3.3 cos曲线
- 向量的内积=W*X=WT*X=|W|*|X|*cos(θ)
1.3.4 内积的最大最小值
最大值
- A*B=|A|*|B|*cos(θ)
- 当其他条件|A| |B| 的模长不变时,
- θ=0°,cos(θ)=1,
- 向量平行/共线,内积最大
- 向量内积最大
最小值
- θ=180°,cos(θ)=-1
- 向量方向相反,内积最小,为负数
1.3.5 内积为正负的判断和应用---可用在机器学习上
- 内积为负
- θ=90-270°之间时,cos(θ)<0,
- 内积为正
- θ=270-(360+90°)之间时,cos(θ)>0,
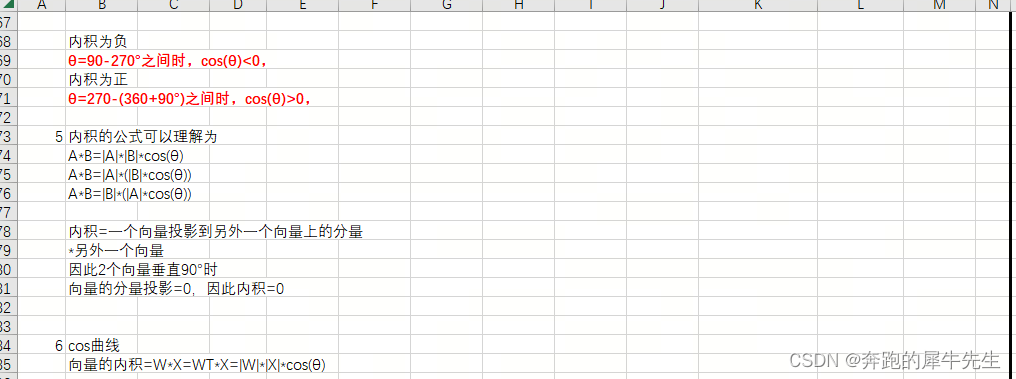
1.3.6 内积的公式可以理解为
- A*B=|A|*|B|*cos(θ)
- A*B=|A|*(|B|*cos(θ))
- A*B=|B|*(|A|*cos(θ))
内积=一个向量投影到另外一个向量上的分量
*另外一个向量
因此2个向量垂直90°时
向量的分量投影=0,因此内积=0
1.4 向量点乘=0时
- 两个向量内积为0 ,必然两个向量垂直/正交
- θ=90°,cos(θ)=0
- 因此垂直,正交时 A*B=0
- θ=90°,cos(θ)=0
- 向量正交垂直,内积并是最小
- 因为内积可以为负数

向量组/矩阵的点乘
2.1 向量组/矩阵的点乘
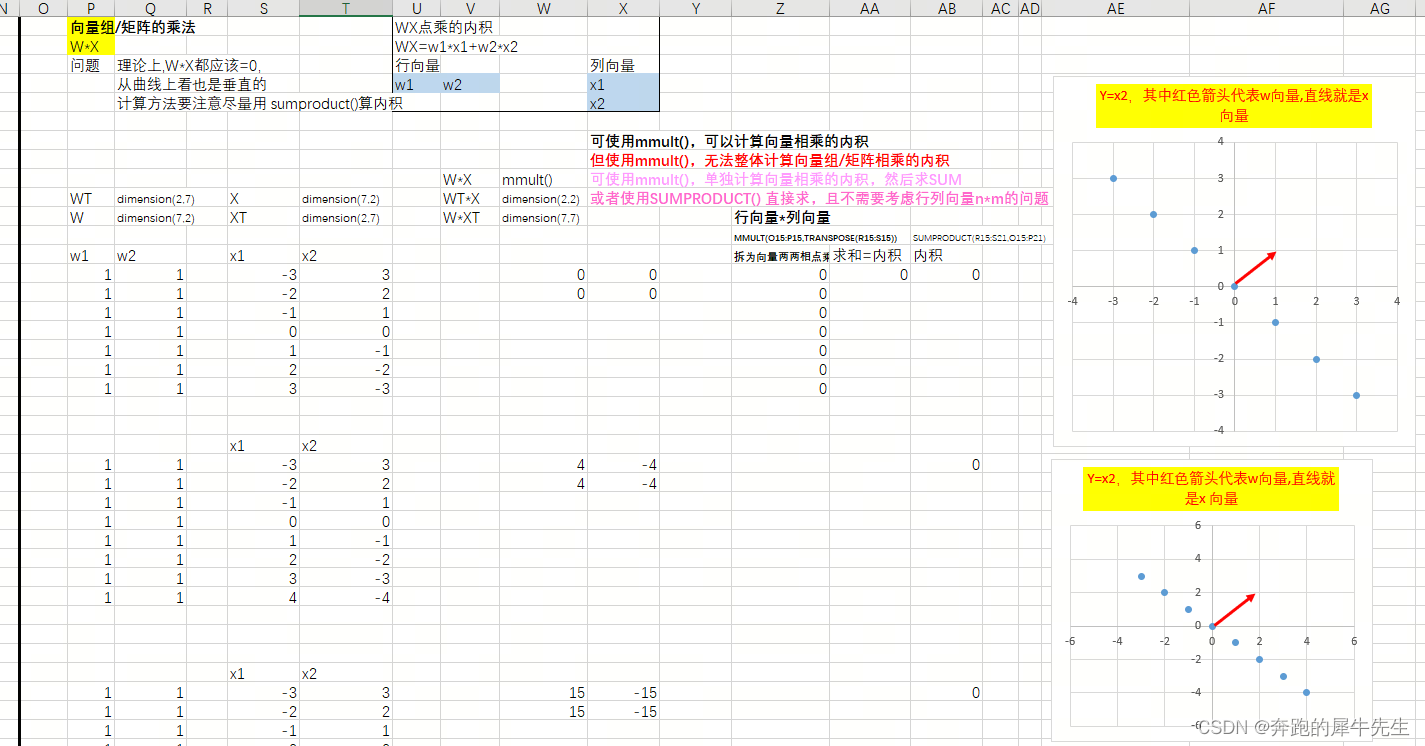
2.2 EXCEL里向量组的乘法
可使用mmult(),可以计算向量相乘的内积
但使用mmult(),无法整体计算向量组/矩阵相乘的内积
可使用mmult(),单独计算向量相乘的内积,然后求SUM
或者使用SUMPRODUCT() 直接求,且不需要考虑行列向量n*m的问题
2.3 公式

2.4 图












)








