---

前言

记录一下 点云学习遇到的一些数学计算方法。

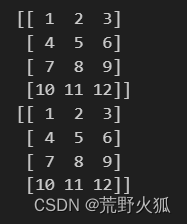
这里点云的在numpy上的形式如下：每个数组里是x,y,z坐标信息。

import numpy as np
points = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
print(points)

---

参考链接
Python之Numpy详细教程
形象理解协方差矩阵【看了很多这个是比较正确的理解】
简而言之，numpy返回一个数组对象，与python中的list不同，拥有更多的操作。
比如：列表不能对[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]列表进行 行列切片。
例如：

import numpy as np
li =[[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
try :print(li[:,0])
except Exception as error:print(error)#报错
shuzu =np.array(li)[:,0] #第一个：表示第一维，第二个0表示第二维的第一个元素 #或者说取第一列
print(shuzu)
print(type(shuzu))
print(list(shuzu))

关于np.array和np.asarray

import numpy as np
points = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
points1 = np.asarray([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
print(points)
print(points1)

返回的数组一致，只是参数上有区别，详情见上面的教程。

一、平均值、方差、协方差

平均值（mean）np.mean()

概念不用多说，这里强调一下写法：

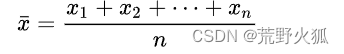
The arithmetic mean of a set of numbers x1, x2, …, xn is typically denoted using an overhead bar, (英文里平均值常写成xbar,bar英文意思是条，带。意思是通常使用个头顶条来表示。)
使用：np.mean() #mean 英译：平均值

import numpy as np
points = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
average_data = np.mean(points, axis=0)##axis=0表示按列求均值
print(average_data)
#[5.5 6.5 7.5]

方差（variance）np.var()

总体方差 np.var(a, ddof=0)

主要看到第一个等号就行，下面推导的是方差也=数平方的均值-数均值的平方

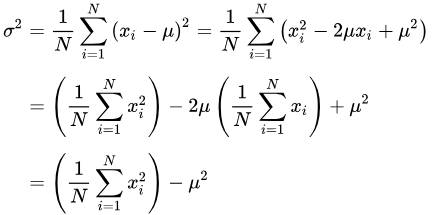
这里u=均值。
np.var()

import numpy as np
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
variance = np.var(a,axis=1) #axis=1表示按行求方差
print(variance)
#[0.66666667 0.66666667 0.66666667 0.66666667]

无偏样本方差np.var(a, ddof=1)

一般来说,点云中计算从方差都是选取部分点云来算方差，所以基本上用无偏样本方差，其中，对n − 1的使用称为贝塞尔校正，它也用于样本协方差和样本标准差（方差的平方根）。详见Wiki百科。定义如下：

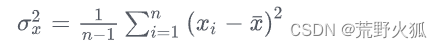
np.var(a, ddof=1) ddof=0表示总体方差，ddof=1表示为样本方差

import numpy as np
a = ([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
sample_variance = np.var(a, ddof=1, axis=1) #ddof=1表示无偏估计
print(sample_variance)
#[1. 1. 1. 1.]

有偏样本方差

则是除以n，这里n为样本大小。与总体方差计算方式一样。

标准差（standard deviation）np.std(a, ddof=1)

standard deviation，缩写为S.D.或σ1。标准差是一种衡量数据分散程度的统计量，它是方差的平方根。
主要用第一种。

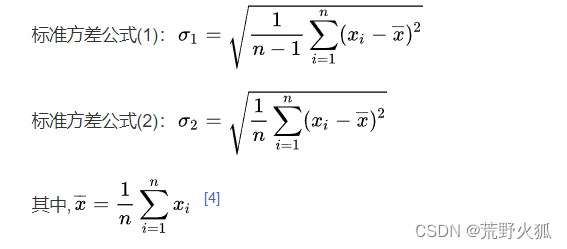
np.std()

import numpy as np #第一种
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
sample_standard_deviation = np.std(a, ddof=1,axis=1) #ddof=1表示无偏估计
print(sample_standard_deviation)
#[1. 1. 1. 1.]

import numpy as np #第二种
a = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
sample_standard_deviation = np.std(a, ddof=0,axis=1) #ddof=0表示有偏估计
print(sample_standard_deviation)
#[0.81649658 0.81649658 0.81649658 0.81649658]

可以验证是方差的开根号。

默认是有偏估计，所以务必加上ddof=1，以下均使用无偏估计（ddof=1）

协方差（covariance）np.cov(x, y,ddof=1)[0][1]

方差衡量单个随机变量（如人口中一个人的身高）的变化，而协方差是衡量两个随机变量一起变化的程度（如一个人的身高和人口中一个人的体重）。

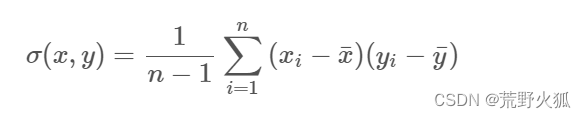
n为样本数量，方差亦可视作随机变量与自身的协方差。

或者 写成如下形式

（图上应为1/n-1）E(x)下面会讲。其中，xi和yi的数量n应相等。

cov为协方差（covariance）的前三个字母缩写。
var为方差（variance）的前三个字母缩写。

与自身的协方差 np.cov(x,ddof=1)

import numpy as np
x = np.array([1, 2, 3, 4, 5])
covxx = np.cov(x,ddof=1)
varx = np.var(x,ddof=1)
print(covx)
print(varx)
'''
2.5
2.5
'''

线性组合的协方差

np.cov(x, y)返回一个协方差矩阵，类似于输出：下面会讲到

[[cov(x,x)],cov[x,y]
[cov(y,x)],cov(y,y)]

所以np.cov(x, y,ddof=1)[0,1] (或[0][1],或[1,0])是x和y的协方差

import numpy as np
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 4, 3, 2, 1])
covariance = np.cov(x, y,ddof=1)# np.cov(x, y)返回一个协方差矩阵，[0, 1]表示x和y的协方差
print(covariance)
print(covariance[0,1])
'''
[[ 2.5 -2.5][-2.5  2.5]]
-2.5
'''

或者用下面一种形式，默认把每一行当作一个变量。

import numpy as np 
x = np.array([[1, 2, 3], [3, 1, 1], [2, 8, 9], [1, 11, 12]])
covariance = np.cov(x,ddof=1)
print(covariance)
'''
[[ 1.         -1.          3.5         5.5       ][-1.          1.33333333 -4.33333333 -7.        ][ 3.5        -4.33333333 14.33333333 23.        ][ 5.5        -7.         23.         37.        ]]
'''

可以看出是个对称矩阵，因为协方差是交换的，即cov(X,Y) = cov(Y,X)。这个矩阵的每个位置都代表了x中两个随机变量的协方差。

用定义的方式验证一下这个函数，当然是对的。

#验证协方差公式
import numpy as np
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 4, 3, 2, 1])
print(np.cov(x, y,ddof=0)[0][0]) #ddof=0表示有偏估计
print(np.cov(x, y,ddof=0)[1][1])
print(np.cov(x, y,ddof=0)[0][1])
covx = np.mean((x - x.mean()) ** 2) #np.mean()求均值 /n
covy = np.mean((y - y.mean()) ** 2)
covxy = np.mean((x - x.mean()) * (y - y.mean()))
print(covx)
print(covy)
print(covxy)
'''
2.0
2.0
-2.0
2.0
2.0
-2.0
'''

如果协方差为正，说明X，Y同向变化，协方差越大说明同向程度越高；如果协方差为负，说明X，Y反向运动，协方差越小说明反向程度越高。

期望值(Expected value) np.average(a, weights=weights)

这里E(X)为期望值：试验中每次可能的结果乘以其结果概率的总和，例如：

由于此时每个点的概率相等，所以也可以写成如上cov(X,Y)形式。

np.average()可以接受一个weights参数，用来计算加权平均值。

import numpy as np
a = np.array([1, 2, 3, 4, 5])
weights = np.array([0.1, 0.2, 0.3, 0.2, 0.2])
weighted_expectation = np.average(a, weights=weights)
print(weighted_expectation)
#3.2

np.mean()与np.average()的区别

import numpy as np
a = np.array([1, 2, 3, 4, 5])
weights = np.array([0.1, 0.2, 0.3, 0.4, 0.5])
mean = np.mean(a)
average = np.average(a, weights=weights)
try :print(a, weights=weights)
except Exception as error:print(error)
print("mean:", mean)
print("average:", average)
'''
'weights' is an invalid keyword argument for print()
mean: 3.0
average: 3.6666666666666665
'''

可以看到，当不指定weights参数时，np.mean()和np.average()的结果是一样的，都是3.0。但是当指定了weights参数时，np.average()会根据每个元素的权重来计算加权平均值，结果是3.6666666666666665。np.mean()不支持weights参数，会报错。

协方差矩阵 （covariance matrix）np.cov(x, y,ddof=1)

交叉协方差矩阵

以下为中文wiki百科中协方差的定义

在统计学与概率论中，协方差矩阵（covariance matrix）是一个方阵，代表着任两列随机变量间的协方差，是协方差的直接推广。
因为是方阵，所以下面的m=n。


英文的wiki百科中交叉协方差矩阵的定义
交叉协方差矩阵
是一个矩阵，其元素在 i、j 位置是随机向量的第 i 个元素与另一个随机向量的第 j 个元素之间的协方差。

后发现这样来理解np.cov()函数理解不了，故查询了英文的wiki百科中协方差矩阵的定义，发现确实有问题，上述定义在英文wiki百科中定义为交叉协方差矩阵，而协方差矩阵定义如下：

协方差矩阵（自协方差矩阵）

英文的wiki百科中协方差矩阵的定义

在概率论和统计学中，协方差矩阵(covariance matrix)，也称为自动协方差矩阵(auto-covariance matrix)、色散矩阵(dispersion matrix)、方差矩阵(variance matrix)或方差-协方差矩阵(variance–covariance matrix)。

是一个平方矩阵，给出给定随机向量的每对元素之间的协方差。任意协方差矩阵都是对称的和半正定的矩阵，且其主对角线包含方差(即每个元素自身的协方差)。不要和交叉协方差矩阵搞混。

直观地说，协方差矩阵将方差的概念推广到多个维度。例如，二维空间中随机点集合的变化不能完全用单个数字来表征，二维空间中随机点的方差也不能用x和y方向包含所有必要的信息;一个2×2矩阵对于充分表征二维变化是必要的。

任何协方差矩阵都是对称的，并且是正半定的，其主对角线包含方差（即每个元素与自身的协方差）。

这里主要按python中的函数来解读了，实际上这样解读更符合直觉上的逻辑。
故可以理解为：

[[cov(x,x)],cov[x,y]
[cov(y,x)],cov(y,y)]

其中covariance_matrix[0,0]和covariance_matrix[1][1]为分别对自身x,和y的协方差。

import numpy as np
x = np.array([1, 2, 3, 4, 5])
y = np.array([5, 4, 3, 2, 1])
covariance_matrix = np.cov(x, y,ddof=1)# np.cov(x, y)返回一个协方差矩阵
print(covariance_matrix)
'''
[[ 2.5 -2.5][-2.5  2.5]]
'''

假设为点云数据形式，实际上和上述一样理解，只不过放在一个数组里了。

import numpy as np #第二种
x = np.array([[1, 2, 3], [3, 1, 1], [2, 8, 9], [1, 11, 12]])
covariance = np.cov(x,ddof=1)
print(covariance)
'''
[[ 1.         -1.          3.5         5.5       ][-1.          1.33333333 -4.33333333 -7.        ][ 3.5        -4.33333333 14.33333333 23.        ][ 5.5        -7.         23.         37.        ]]
'''

可以看出上述协方差矩阵为对称的。

协方差矩阵=A^TA的证明

更多可参考
理解和分析协方差矩阵
形象理解协方差矩阵 （有关于是正半定矩阵的证明）

二、奇异值分解、主成分分析法

奇异值分解（Singular Value Decomposition）np.linalg.svd()

这篇大佬讲的很细，可以参考通俗易懂。
SVD分解
这里仅在此基础上做些概念上的补充，简化理解过程，及错误的勘误。

补充： 奇异值和特征值

特征值和特征向量是方阵的概念，它们表示矩阵作用于某些向量时，只会改变向量的长度，不会改变向量的方向。
特征值是这些向量的长度缩放比例，特征向量是这些向量的方向。
特征值和特征向量可以用来分解方阵为对角矩阵和正交矩阵的乘积，这样可以简化矩阵的运算和理解矩阵的性质。

奇异值和奇异向量是任意矩阵的概念，它们表示矩阵作用于某些向量时，会使向量的长度达到最大或最小。
奇异值是这些向量的长度，奇异向量是这些向量的方向。
奇异值和奇异向量可以用来分解任意矩阵为对角矩阵和两个正交矩阵的乘积，这样可以用来降维、压缩、去噪等应用。

简而言之：奇异值是对特征值在矩阵上的推广，将方阵推广到了任意矩阵

奇异值分解能够用于任意mxn矩阵，而特征分解只能适用于特定类型的方阵，故奇异值分解的适用范围更广。

补充：奇异矩阵和非奇异矩阵(线代基础知识)

奇异矩阵和非奇异矩阵是线性代数中的概念，它们都是指方阵，即行数和列数相等的矩阵。
奇异矩阵是指行列式为0的矩阵，也就是说它的秩不是满秩，或者它的特征值有0。
非奇异矩阵是指行列式不为0的矩阵，也就是说它的秩是满秩，或者它的特征值都不为0。
非奇异矩阵也称为可逆矩阵，因为它们都有唯一的逆矩阵。

补充：酉矩阵和正交矩阵

酉矩阵和正交矩阵都是一种特殊的方阵，它们的转置矩阵等于它们的逆矩阵，也就是说它们都满足A^T = A^-1。
但是，酉矩阵是复数方阵，它的转置矩阵要求是共轭转置，也就是说它满足A^H = A^-1， 其中A^H 表示A的共轭转置。

正交矩阵是实数方阵，它的转置矩阵不需要是共轭的，也就是说它满足A^T = A^-1。

简而言之：酉矩阵是正交矩阵的推广，当酉矩阵的元素都是实数时，它就是正交矩阵。满足A^T A = AA^T =E

从特征值分解到奇异值分解

学过线代的我们都知道，若A~ ^ (^ 为对角矩阵 ) 则P^-1AP =^,(P为可逆矩阵）
可以推到A = P ^ P^-1, 此时由相似的性质可以得到A的特征值＝^的特征值，且一一对应其特征向量的位置。说不太清，下面开始手推。
特征值分解：
定义为：

A为方阵(nxn)，W为正交矩阵，（正交默认单位化了，即行向量，列向量都是正交的单位向量。），中间Σ为对角矩阵（nxn）（也叫特征值矩阵）。

最后的^ 里即为A(nxn)的特征值。
奇异值分解：
定义为:

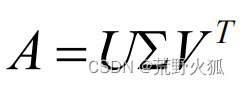
U(m×m酉矩阵)，Σ(m×n)，除了主对角线上的元素以外全为零，主对角线上的每个元素都称为奇异值，V是一个n×n的酉矩阵。

SVD分解

求特征值 eig_val, eig_vec = np.linalg.eig(A）

返回第一个值为特征值数组，第二个特征向量矩阵。注意特征值不一定是有序排列，但特征向量返回的默认是单位向量。eig 是特征值（eigenvalue）的缩写

求索引值 index =np.argsort(x)

输出的结果是x数组中的元素从小到大排序后的索引数组值。
[::1]为倒序排列，在列表形式的数据中，也能排列。

import numpy as np# 定义一个3x2的矩阵A
A = np.array([[0, 1], [1, 1], [1, 0]])
print(A)# 求AAT的特征值和特征向量
AAT = np.dot(A, A.T)
print(AAT)
eig_val, eig_vec = np.linalg.eig(AAT) #默认返回单位向量
print(eig_val)
print(eig_vec)# 按特征值的大小降序排列，调整特征向量的顺序
idx = eig_val.argsort()[::-1]
eig_val = eig_val[idx]
eig_vec = eig_vec[:, idx]U=eig_vec
print(U)# 求ATA的特征值和特征向量
ATA = np.dot(A.T, A)
print(ATA)
eig_val, eig_vec = np.linalg.eig(ATA)
print(eig_val)
print(eig_vec)# 按特征值的大小降序排列，调整特征向量的顺序
idx = eig_val.argsort()[::-1]
eig_val = eig_val[idx]
eig_vec = eig_vec[:, idx]V=eig_vec
print(V)# 求奇异值，构成Σ
Sigma = np.diag(np.sqrt(eig_val))
print(Sigma) #默认shape是与行列的较小值的方阵#理应shape与输入矩阵A相同
Sigma = np.append(Sigma, np.zeros((1, A.shape[1])), axis=0)
print(Sigma)# 验证A=UΣV*
print(np.dot(U, np.dot(Sigma, V.T))) #特征向量不唯一导致的'''
[[0 1][1 1][1 0]]
[[1 1 0][1 2 1][0 1 1]]
[ 3.00000000e+00  1.00000000e+00 -5.13860489e-17]
[[-4.08248290e-01  7.07106781e-01  5.77350269e-01][-8.16496581e-01  2.48915666e-16 -5.77350269e-01][-4.08248290e-01 -7.07106781e-01  5.77350269e-01]]
[[-4.08248290e-01  7.07106781e-01  5.77350269e-01][-8.16496581e-01  2.48915666e-16 -5.77350269e-01][-4.08248290e-01 -7.07106781e-01  5.77350269e-01]]
[[2 1][1 2]]
[3. 1.]
[[ 0.70710678 -0.70710678][ 0.70710678  0.70710678]]
[[ 0.70710678 -0.70710678][ 0.70710678  0.70710678]]
[[1.73205081 0.        ][0.         1.        ]]
[[1.73205081 0.        ][0.         1.        ][0.         0.        ]]
[[-1.00000000e+00  2.22044605e-16][-1.00000000e+00 -1.00000000e+00][-1.11022302e-16 -1.00000000e+00]]
'''

np.linalg.svd()

import numpy as np# 定义一个3x2的矩阵A
A = np.array([[0, 1], [1, 1], [1, 0]])
print(A)# 使用linalg.svd函数进行奇异值分解
U, S, V = np.linalg.svd(A)# 打印结果
print("U:", U)
print("S:", S)
print("V:", V)# 使用diag函数构造对角矩阵Σ
Sigma = np.diag(S)
print("Sigma:", Sigma)
'''
[[0 1][1 1][1 0]]
U: [[-4.08248290e-01  7.07106781e-01  5.77350269e-01][-8.16496581e-01  5.55111512e-17 -5.77350269e-01][-4.08248290e-01 -7.07106781e-01  5.77350269e-01]]
S: [1.73205081 1.        ]
V: [[-0.70710678 -0.70710678][-0.70710678  0.70710678]]
Sigma: [[1.73205081 0.        ][0.         1.        ]]
'''

勘误：SVD分解
如上，我们不能得出特征值矩阵等于奇异值矩阵的平方,他们连矩阵的nxm形式都不同，只能说：如果奇异值矩阵Σ的行数与特征值矩阵相等，才能得到如此说法，由它的例子也可以看出，不过由上述手推和怕python返回值上来说，也可以接受这种说法。

奇异值的物理意义 （为什么要进行奇异值分解）

奇异值的物理意义
我们为什么要进行奇异值分解，以及为什么选取前几个较大的奇异值可以代表举证的主要信息，而后面的较小的奇异值则可以忽略或近似为零，这样可以实现矩阵的降维、压缩、去噪等目的。

主成分分析法（Principal components analysis）

补充：归一化 ：（常见）将数据映射到 [0,1] or [-1.1] 的区间之内

由此可见归一化为很多种，常见的是指最小、最大特征缩放。

1、映射到[0,1]范围内：
每一项减去最小值后都除以最大值与最小值之差

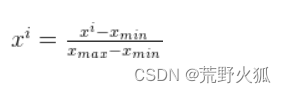
2、映射到[-1,1]范围内：
[0,1]->[0,2]->[-1,1]

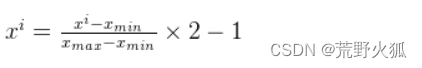
补充：去中心化：以平均值为中心移动至原点

使数据每一项都减去均值：

补充：标准化：使得方差为1，均值为0

去中心化后，除以标准差。

步骤

主要基于维基百科，部分参考：
主成分分析（PCA）原理详解
手撸PCA(Python七行代码实现）

第一个主成分可以等效地定义为使投影数据方差最大化的方向。在以上奇异值分解的基础上，可以理解为最大的特征值所对应的特征向量。
第二主成分可以理解为第二大特征值所对应的特征向量，以此类推。

第一步：
去中心化。
原数据[[1, 2, 3], [3, 1, 1], [2, 8, 9], [1, 11, 12]],求取列方向的均值（求行向量没有意义，行向量为单个点的[x,y,z]数据）。然后将其减掉。
也可以进行标准化，这里仅中心化。

通常，为了确保第一主成分描述的是最大方差的方向，我们会使用平均减法（去中心化）进行主成分分析。如果不执行平均减法，第一主成分有可能或多或少的对应于数据的平均值。另外，为了找到近似数据的最小均方误差，我们必须选取一个零均值。

PCA 的结果取决于变量的缩放。这可以通过按标准差缩放每个特征来解决这个问题，从而最终得到具有单位方差的无量纲特征。（也就是说标准化，可以得到位方差的无量纲特征）

在某些应用中，每个协方差矩阵的列向量，也可以缩放为方差等于 1（标准化）。这一步会影响计算出的主成分，但使它们独立于用于测量不同变量的单位。

一般来说，如果数据的各个特征的量纲和尺度相差不大，或者数据的分布比较均匀，那么只需要去中心化就可以了。如果数据的各个特征的量纲和尺度相差很大，或者数据的分布比较偏态，那么最好进行标准化，以提高PCA的效果和稳定性。

第二步：
计算协方差矩阵。
计算X^TX 就可以得到协方差矩阵。（参见协方差矩阵=A^TA的证明）
Gram matrix

A^TA又被称为Gramian矩阵

这里（A^TA的一些探讨）
在维基百科中的公式如下：

看到很多的博客上没有除以n-1。

个人看法：至于为什么不除以n-1，在探究特征向量时，n-1不影响结果，在研究贡献率时（每个特征值占所有特征值和），也不影响结果。
当然研究特征值时会有影响，但一般在数值上大多数涉及到百分比率时，变无关紧要了，还有就是A^TA也是协方差矩阵。
对是否要/n-1，持保留意见。

第三步：
通过SVD计算协方差矩阵的特征值与特征向量。
第四步：
降序排序
第五步：
求贡献率：每个主成分对整体特征影响了多少百分比。

下面仅进行去中心化操作。

import numpy as np
A = np.array([[1, 2, 3], [3, 1, 1], [2, 8, 9], [1, 11, 12]])
#1、去中心化
average = np.mean(A, axis=0)
decentration_matrix = A - average #去中心化
std=np.std(A, axis=0,ddof=1)
#decentration_matrix = decentration_matrix/std #标准化        
print(decentration_matrix)
#2、求协方差矩阵
H = np.dot(decentration_matrix.T, decentration_matrix)  # 求协方差矩阵
print(H)
#3、求协方差矩阵的特征值和特征向量
eigenvectors, eigenvalues, eigenvectors_T = np.linalg.svd(H) 
print(eigenvalues)
#4、降序排列特征值，调整特征向量的顺序
index = eigenvalues.argsort()[::-1] # 从大到小排序 .argsort()是升序排序，[::-1]是将数组反转，实现降序排序
eigenvalues = eigenvalues[index] # 特征值  ## 使用索引来获取排序后的数组
print(eigenvalues)
eigenvectors = eigenvectors[:, index] # 特征向量
print(eigenvectors)
#5、贡献率
contribution_rate = eigenvalues / eigenvalues.sum()
print(contribution_rate)
'''
[[-0.75 -3.5  -3.25][ 1.25 -4.5  -5.25][ 0.25  2.5   2.75][-0.75  5.5   5.75]]
[[ 2.75 -6.5  -7.75][-6.5  69.   73.5 ][-7.75 73.5  78.75]]
[1.48237664e+02 2.20024983e+00 6.20861128e-02]
[1.48237664e+02 2.20024983e+00 6.20861128e-02]
[[-0.06925606 -0.96162402  0.26548605][ 0.68147921 -0.23995698 -0.69138031][ 0.72855315  0.13304095  0.67194525]]
[9.84967868e-01 1.46196002e-02 4.12532311e-04]
'''

为什么要进行主成分分析

中文翻译后再看这个
理解主成分分析、特征向量和特征值 打的比喻生动形象。