1: 确定 Use Case 和 约束

Use Cases

• User 搜索某人然后看到被搜索人的最短路径
• Service 有高可用

约束和假设

状态假设

1. Traffic 不是平均分布的

• 一些被搜索者是更加受欢迎的，某些被搜索者只会被搜索一次
• 图数据不适用与单个机器
• 图的分布是轻量级的
• 一亿个 User
• 每个 User 平均有 50 个朋友
• 十亿个搜索每个月

练习使用更传统的系统 - 不要使用 graph-specific solutions, 比如 GraphQL 或者 图数据库 Neo4j

计算使用量

1. 50 亿 朋友关系
   • 一亿 users * 50 个 friends / user
2. 每秒 400 个搜索请求

便利转换索引：

• 每个月250 万秒
• 1 个请求 / s = 250 万请求 / 月
• 40 个请求 / s = 1 亿请求 / 月
• 400 个请求 / s = 10 亿 请求 / 月

2：创建一个 High Level 设计

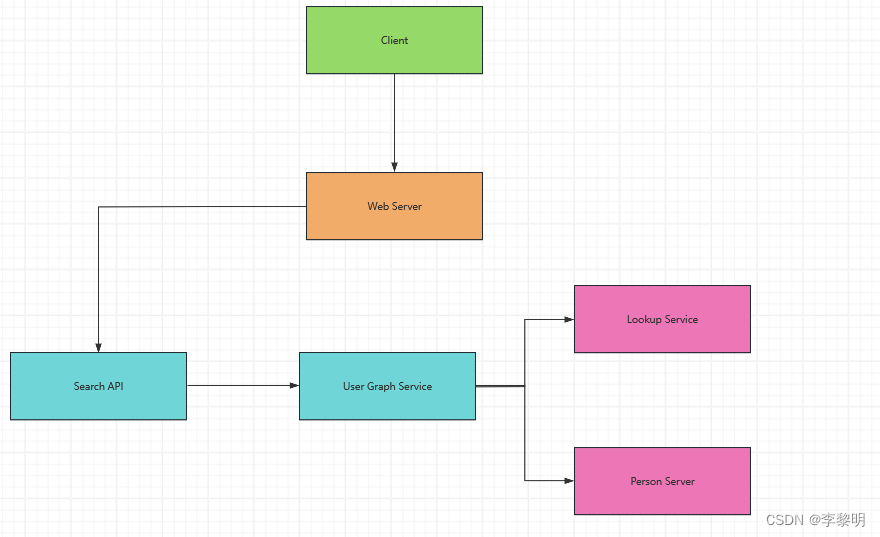
3: 设计核心组件

Use Case: User 搜索某人，然后得到被搜索人的最短路径

没有上百万 User 和 数十亿 friend 关系的限制，我们可以解决最短路径问题通过使用 BFS 算法

class Graph(Graph):def shortest_path(self, source, dest):if source is None or dest is None:return Noneif source is dest:return [source.key]prev_node_keys = self._shortest_path(source, dest)if prev_node_keys is None:return Noneelse:path_ids = [dest.key]prev_node_key = prev_node_keys[dest.key]while prev_node_key is not None:path_ids.append(prev_node_key)prev_node_key = prev_node_keys[prev_node_key]return path_ids[::-1]def _shortest_path(self, source, dest):queue = deque()queue.append(source)prev_node_keys = {source.key: None}source.visit_state = State.visitedwhile queue:node = queue.popleft()if node is dest:return prev_node_keysprev_node = nodefor adj_node in node.adj_nodes.values():if adj_node.visit_state == State.unvisted:queue.append(adj_node)prev_node_keys[adj_node.key] = prev_node.keyadj_node.visit_state = State.visitedreturn Node

我们不能把所有的 User 都放在同一个机器里面，我们需要 分片的 User (通过 Person Server)
而且使用 Lookup Service 去访问他们

1. Client 发送请求到 Web Server
2. Web Server 转发请求到 Search API server
3. Search API server 转发请求到 User Graph Service
4. User Graph Service 做下面的事情：
   • 使用 Lookup Service 去寻找 Person Server, 当当前 User的info 被存储过后
   • 寻找合适的 Person Server去接收当前 User的 friend_ids 的 list
   • 运行 BFS 搜索（使用当前 User 作为 source, 而且当前 User的 friend_ids 作为 ids）
   • 从给定的 id 获取 adjacent_node
     • User Graph Service 将需要再次和 Lookup Service沟通，去决定哪一个 Person Service 存储 adjecent_node 数据（匹配给定的 id）

Lookup Service 实现：

class LookupService(object):def __init__(self):self.lookup = self._init_lookup()  # key: person_id, value: person_serverdef _init_lookup(self):...def lookup_person_server(self, person_id):return self.lookup[person_id]

Person Server 实现：

class PersonServer(object):def __init__(self):self.people = {}  # key: person_id, value: persondef add_person(self, person):...def people(self, ids):results = []for id in ids:if id in self.people:results.append(self.people[id])return results

Person 实现：

class Person(object):def __init__(self, id, name, friend_ids):self.id = idself.name = nameself.friend_ids = friend_ids

User Graph Service 实现：

class UserGraphService(object):def __init__(self, lookup_service):self.lookup_service = lookup_servicedef person(self, person_id):person_server = self.lookup_service.lookup_person_server(person_id)return person_server.people([person_id])def shortest_path(self, source_key, dest_key):if source_key is None or dest_key is None:return Noneif source_key is dest_key:return [source_key]prev_node_keys = self._shortest_path(source_key, dest_key)if prev_node_keys is None:return Noneelse:# Iterate through the path_ids backwards, starting at dest_keypath_ids = [dest_key]prev_node_key = prev_node_keys[dest_key]while prev_node_key is not None:path_ids.append(prev_node_key)prev_node_key = prev_node_keys[prev_node_key]# Reverse the list since we iterated backwardsreturn path_ids[::-1]def _shortest_path(self, source_key, dest_key, path):# Use the id to get the Personsource = self.person(source_key)# Update our bfs queuequeue = deque()queue.append(source)# prev_node_keys keeps track of each hop from# the source_key to the dest_keyprev_node_keys = {source_key: None}# We'll use visited_ids to keep track of which nodes we've# visited, which can be different from a typical bfs where# this can be stored in the node itselfvisited_ids = set()visited_ids.add(source.id)while queue:node = queue.popleft()if node.key is dest_key:return prev_node_keysprev_node = nodefor friend_id in node.friend_ids:if friend_id not in visited_ids:friend_node = self.person(friend_id)queue.append(friend_node)prev_node_keys[friend_id] = prev_node.keyvisited_ids.add(friend_id)return None

我们可以使用 public REST API:

$ curl https://social.com/api/v1/friend_search?person_id=1234

Response:

{"person_id": "100","name": "foo","link": "https://social.com/foo",
},
{"person_id": "53","name": "bar","link": "https://social.com/bar",
},
{"person_id": "1234","name": "baz","link": "https://social.com/baz",
}

4: 扩展设计

我们可以有以下优化点：

• 存储完整或部分BFS遍历，以加速后续在内存缓存中的查找
• 批处理计算然后存储完整或部分BFS遍历，加速在 NoSQL 数据库中的子序列查询
• 减少机器跳跃通过批量查找朋友在同一个域名下的 Person Server
  • 通过Location分片的 Person Server去进一步的提高，正如朋友普遍都住的比较近
• 在同一时刻做两个 BFS 搜索，一个从 source开始，另一个从 destination 开始，然后 merge 这量个 path
• 人们从 BFS 开始搜索大量的 friend. 然后他们是更喜欢去减少 分页的数字（在当前用户和搜索结果）
• 在询问用户是否要继续搜索之前，根据时间或跳数设置一个限制，因为在某些情况下，搜索可能需要相当长的时间
• 使用Neo4j等图形数据库或GraphQL等特定于图形的查询语言（如果没有限制阻止使用图形数据库）