第五章 特征值和特征向量
第一节、特征值和特征向量的基本概念
一、特征值和特征向量的理论背景
在一个多项式中,未知数的个数为任意多个,且每一项次数都是2的多项式称为二次型,二次型分为两种类型:即非标准二次型及标准二次型

注意:
①二次型X^T AX为非标准二次型的充分必要条件是A^T=A 但A为非对角矩阵;二次型 X^TAX为标准二次型的充分必要条件是A 为对角矩阵.
②将非标准二次型 X^TAX 化为标准二次型等价于将矩阵A对角化,特征值与特征向量的理论即矩阵对角化理论,
二、基本概念
①特征值与特征向量
设A为n阶矩阵,若存在常数λ及n维非零列向量α使得Aα=λα,称λ为矩阵A的特征值,α为矩阵A的属于特征值入的特征向量
注意:
Aα=λα等价于(λE-A)α=0,由α为非零向量,得方程组(λE-A)X=0有非零解,从而有r(λE-A)<n,或|λE-A|=0,即:若λ为矩阵A的特征值,则一定有|λE-A|=0;反之,若|λE-A|=0,则齐次线性方程组(λE-A)X=0有非零解,从而存在非零向量α,使得(λE-A)α=0,或Aα=λα,故λ为矩阵A的特征值,
②特征方程

注意:

③相似矩阵
设A,B为n阶矩阵,若存在可逆矩阵P,使得P^-1AP=B,称矩阵A与矩阵B相似,记为A~B;若存在可逆矩阵P,使得 P^-1AP=A,其中A为对角矩阵,则称A可以相似对角化.
矩阵相似常见的性质有:
(1)A ~ A
(2)若A ~ B,则B ~ A
(3)若A~B ,B ~ C,则A ~ C
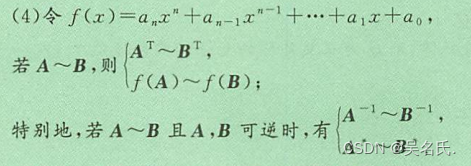
(5)若A ~ B相似,则r(A)=r(B),反之不对
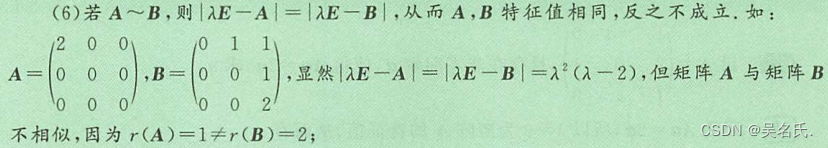
(7)若A ~ B,则|A|=|B|且tr(A)=tr(B),tr(A)指的是矩阵A的迹
④施密特正交化
把一组线性无关的向量组转化为一组两两正交且规范的向量组的过程称为施密特正交化
设α1,α2,…,αn线性无关,施密特正交化过程分为两个步骤:
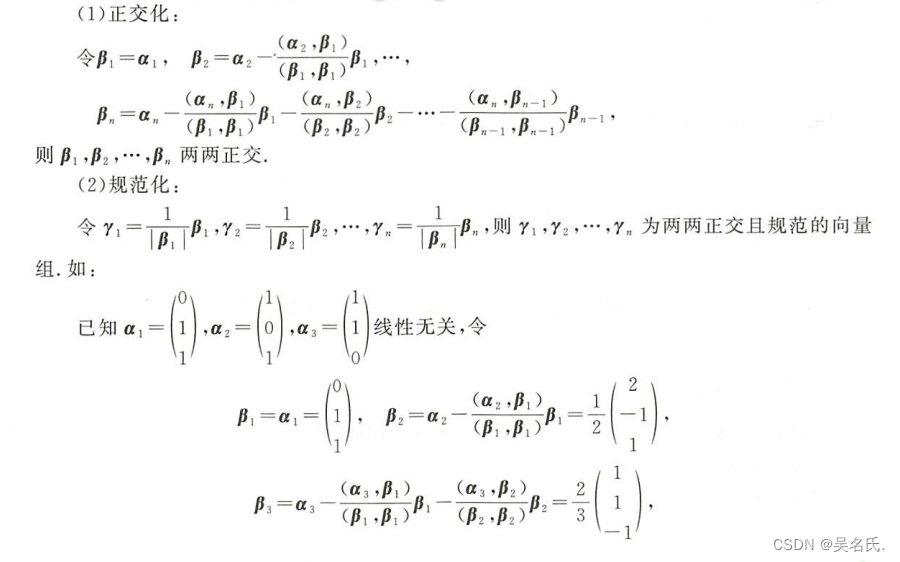
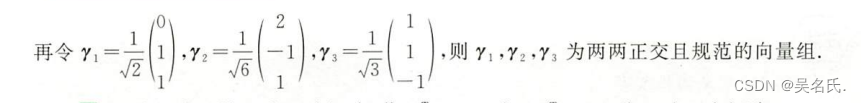
⑤正交矩阵
设Q为n阶矩阵,若Q^TQ = E(或Q^QT=E),称Q为正交矩阵
注意:
(1)若Q为正交矩阵,则 Q^-1= Q^T
(2)设Q=(γ1,γ2,…,γn)为n阶矩阵,则Q为正交矩阵的充分必要条件是γ1,γ2,…,γn为两两正交的规范向量组
(3)若Q为正交矩阵,则|Q| =1或-1;
(4)若Q为正交矩阵,则Q的特征值为一1或1;
(5)若Q为正交矩阵,且Y=QX(其中X,Y为向量),则|Y|=|X|
第二节、特征值和特征向量的性质
一、特征值与特征向量的一般性质
定理1 设A为n阶矩阵λ1,λ2,…,λn为A的特征值,则有
(1)λ1+λ2+…+λn=tr(A)
(2)λ1λ2…λn=|A|
注意:A可逆 等价于 |A|≠0 等价于 λi≠0(1≤i≤n)
定理2 设A是n阶矩阵,λ0为A的k阶特征值,则
(1)若k=1,即λ0为单特征值,则属于特征值λ0的线性无关的特征向量只有一个
(2)若k>1,则属于特征值λ0的线性无关的特征向量个数不超过k个

定理4 设A为n阶矩阵,则A的不同特征值对应的特征向量线性无关
定理5 设A为n阶矩阵,则A可相似对角化(或与对角矩阵相似)的充分必要条件是A有n个线性无关的特征向量.
定理6 设A为n阶矩阵,λ1,λ1,为A的两个不相等的特征值,又Aα=λ1α,Aβ=λ2β(α,β为非零向量),对任意的a≠0,b≠0,向量aα+bβ一定不是特征向量
二、实对称矩阵特征值与特征向量的性质
定理1 设A为实对称矩阵,则A的特征值都是实数
定理2 设A为实对称矩阵,则A的不同特征值对应的特征向量正交

第三节 矩阵对角化理论
一、一般矩阵的相似对角化

二、实对称矩阵的相似对角化
①实对称矩阵对角化定理
定理1 设A^T=A(说明是实对称矩阵),则A一定可以相似对角化

②实对称矩阵相似对角化过程

注意:

特征值和特征向量笔记
①A=P^-1BP,则B的特征向量为: P^-1a1, P^-1a2,…, P^-1an
②B和B+nE的特征向量一致





)






)






