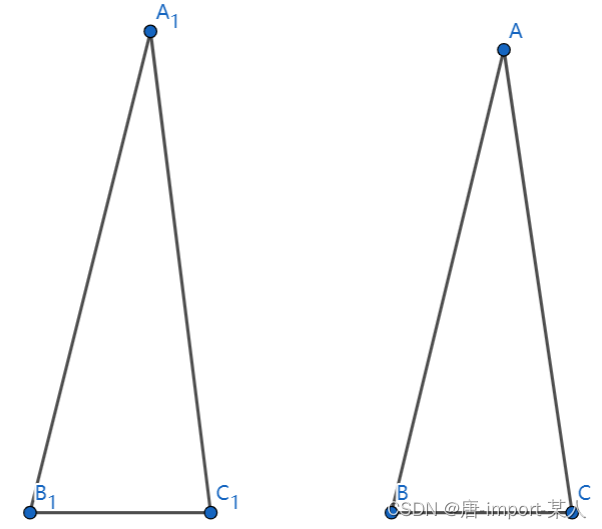
一.有两角夹一边分别相等的两个三角形全等

数学证明:

• $设△ABC与△A_1{B}_1{C}_1\angle B=\angle B_1,\angle C=\angle C_1,B_1{C}_1=BC$
• $①移动\angle B_1与\angle B重合,边B_1{C}_1取BC方向$
• $②\because B_1{C}_1=BC,\therefore \angle C_1与\angle C重合$
• $③\because \angle B_1与\angle B重合,\angle C_1与\angle C重合,B_1{C}_1=BC$
• $④\therefore \angle A_1=\angle A$
• $\therefore △ABC≌△A_1{B}_1{C}_1$
  解释:
• 首先，将第二个三角形移动，使得它的一个角与第一个三角形的相应角重合。
• 接着，由于两个三角形的一个边相等，我们可以推断出它们的另一个角也相等。
• 最后，由于两个三角形现在有两个角和一个边分别相等，根据三角形全等的定理，我们可以得出这两个三角形是全等的。

二.有两边夹一角分别相等的两个三角形全等

数学证明:
$设△ABC与△A_1{B}_1{C}_1\angle A=\angle A_1,A_1{B}_1=AB,A_1{C}_1=AC$
$①移动\angle A_1与\angle A重合,边A_1{B}_1取AB方向,边A_1{C}_1取AC方向$
$②\because A_1{B}_1=AB,\angle A=\angle A_1,点B_1重合点B$
$③\therefore A_1{C}_1=AC,\angle A=\angle A_1,点C_1重合点C$
$\therefore △ABC≌△A_1{B}_1{C}_1$

解释:

• 首先，将第二个三角形移动，使得它的一个角与第一个三角形的相应角重合。
• 接着，由于两个三角形的两个边相等，我们可以推断出它们的另一个边也相等。
• 最后，由于两个三角形现在有两个边和一个角分别相等，根据三角形全等的定理，我们可以得出这两个三角形是全等的。

三.三边相等的两个三角形全等

$设△ABC与△A_1{B}_1{C}_1,A_1{B}_1=AB,A_1{C}_1=AC,B_1{C}_1=BC$
数学证明:

• ①移动$△A_1{B}_1{C}_1$的$A_1{B}_1$与$△ABC$的$AB$重合,且两个三角形都置于同向
• $②\because A_1{C}_1=AC,\therefore 点C_1重合点C否则会出现A_{1}C=A_1{C}_1的等腰三角形,C_{1}C平行且相交AC这是不可能的$
• $③\because B_1{C}_1=BC,点B_1重合点B$
• $\therefore △ABC≌△A_1{B}_1{C}_1$

解释:

• 首先，将第二个三角形移动，使得它的一个边与第一个三角形的相应边重合。
• 接着，由于两个三角形的两边相等，我们可以推断出它们对应的角相等
• 最后，由于两个三角形现在有三边分别相等，根据三角形全等的定理，我们可以得出这两个三角形是全等的。