对于环形链表是否存在环的做法，普通算法可以通过额外Hash数组来存储链表元素，直到Hash数组中出现重复元素。时间复杂度O(n)，空间复杂度O(n)

Floyd判圈算法通过利用快慢指针的移动来实现，时间复杂度O（n），空间复杂度O（1）

一、环形链表

这个不需要过过多的介绍，环形链表就是存在一个节点被2个节点指向，形成了一个闭环。

需要注意的是，一个节点可以被两个节点指向，但是不可能一个节点指向多个节点，所以不会出现一下情况：

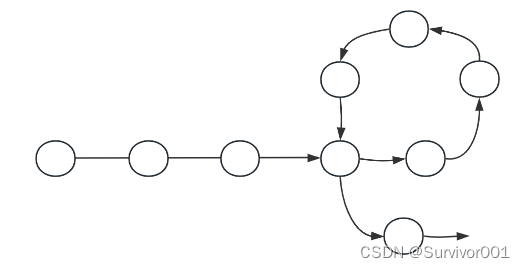
二、算法结论

存在不同速度的快慢指针（slow & fast），慢指针每周期移动1个节点，快指针每周期移动2节点

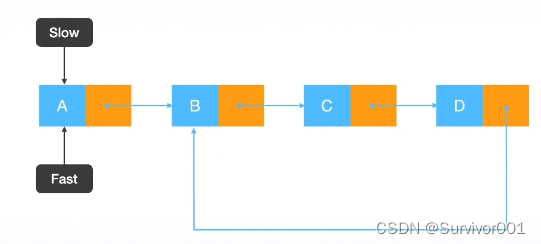
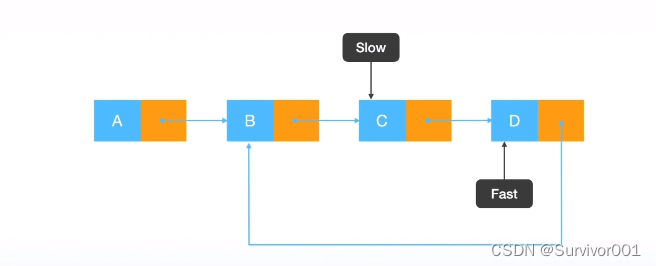
1、因为快指针比慢指针速度快，所以如果链表中不存在环时，快慢指针永远不得相遇，直到Fast移动到尾部结束，时间复杂度O（n），因为Fast指针速度是Slow指针两倍，所以当Fast指针到达尾部时，Slow指针走了一半，即S指向中间值。

2、如果存在环，Fast先进入到环内，并开始做绕环移动，Slow和Fast在环内经过n次移动后，必然会相遇

3、快慢指针在环内第一次相遇后，将其中一个指针重置到head位，当他们再次相遇后指向的节点为入环节点

三、算法证明

1、每次循环，为什么快慢指针一定要快1步，是否可以前进更多？（Slow前进1格，Fast前进2格）

这是因为快慢指针如果相距更多的步，可能存在环内永远不会相遇的情况，比如慢指针前进1格，快指针前进4格时，如下

因为环节点数据量为3个，所以对于Fast指针来说每次循环等于前进1格，而慢指针也前进1格，所以两者永远不能相遇。

因此想要快慢指针在环内能必然或者更快的相遇，那需要他们每次循环后，距离-1，直到相遇。F指针比S指针快1步，可以更好的保障其在环境一定能够相遇，或者更早的相遇。

2、为什么快慢指针在环内一定会相遇？

假如快慢指针此时都在环内，他们相距距离为N，因为环是无限循环的，假设次数S指针在F指针前，即S-F=N

 因为F指针比S指针快1步，所以进行1次移动后：

S+1-(F+2) = S-F -1 = N-1 ，即执行一次后两者的距离-1，因此在n次循环后，必然会出现相遇。

此时如果将设F指针速度为vf， 慢指针速度为vs，同时要确保一定相遇满足N-1，则：

S+vs -(F +vf) = N-1   

  --> S-F + vs-vf = n-1  

  --> vs - vf = 1，即相差1步

同时N为两者的距离，肯定是小于环的长度的，所以在S指针进环后，第1圈内一定会相遇

结论：

首先F指针每次比S指针快1步，可以确保在环中一定可以相遇，如果快更多，则不能保证或需要更多的循环。

3、入口节点结论证明

上面已经证明了F\S在环中一定是能够相遇的，且S进环后，第一圈一定会相遇，那么假设F\S

在P点相遇

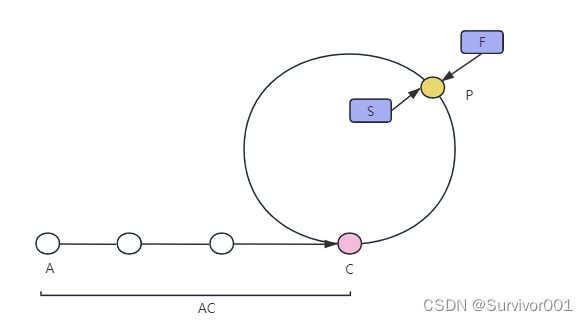
因为F比S快1步，所以F在环内已经跑了1圈了

因此F行驶距离：AC + 2CP + PC

S行驶距离：AC + CP

因为F速度为S的两倍，因此 AC + 2CP + PC = 2（AC + CP）得出 AC = PC

即：在第一次相遇时，PC和AC的长度是一样的，因此此时将任意节点重置到A位，并两者均以相同的速度前进，必然会在C点相遇，因此C点为入口点。

4、原理理解了算法就比较简单了

判断单向链表是否存在环，且返回入环节点

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public int hasCycle(ListNode head) {if(head == null){return -1;}ListNode fast = head;ListNode slow = head;// 第一次相遇while(true){if(slow.next == null  || fast.next == null ){return false;}fast = fast.next.next;slow = slow.next;if(fast == slow){break;}} // 第二次相遇 while(fast!=slow){fast = fast.next;slow = slow.next;if(fast == slow){return fast ;}} }
}

 总结:

Floryd算法是快慢指针算法一种实现，快慢指针 | 双指针算法思想用法非常广泛，比如上述提到的找到中间位数、删除倒数第N节点等等