今天又来更新啦，准备蓝桥杯的小伙伴可以和我一起来刷题，建议大家先看题，整理出思路，再看如何用简单的写法将思路构建出来，然后优化细节，找到解决某些例外出现的方法，从而成功解答这道题。
快乐数<-题目链接
做题思路：
首先观察成功的情况
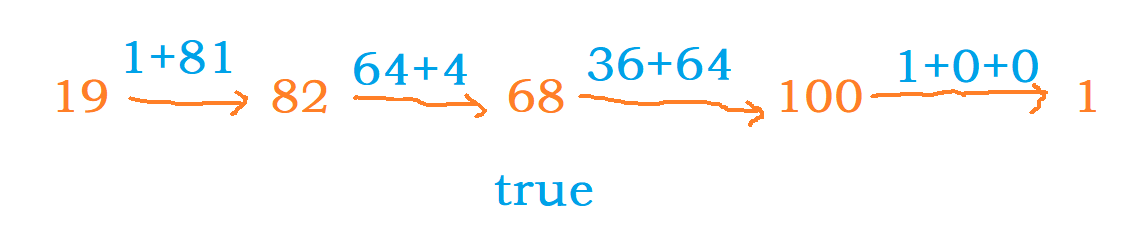
只要当结果为1时，就返回true。
这种情况，就发现在运算过程中会进入一个循环，但这个循环中不会出现1，这样就返回false。
思路
首先我们来验证为什么不会出现出现无限不循环的情况。
要知道这道题的范围
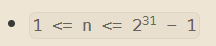
数据的最大范围2的十次方为1024,2的31次方大概为102410241024，我们就直接假设为9999999999，他的下一位为810。
鸽巢原理
有x个鸽子窝，有x+1只鸽子，那么至少有一个鸽子窝里有两只鸽子。
所以说，不管n的值为多少，n在变化的过程后一定是会小于810的，这个结论我想大家一定明白。
现在我们随便给一个数，让他计算811次，在计算的过程中由于不是循环的，所以会产生811个新的数据，然而我们的变化范围是1~810所以和实际不符合，所以这个计算过程一定是循环的。
OK，现在我们已经知道数据计算的过程一定是一个循环，不知道大家做过这样一道题目没，判断一个链表是否带环，我们的写法通常是实现双指针从而求解。
对于这道题，我们就还是使用双指针算法的思想。
不同的是，对于链表处的快指针走两步，这里的是运算两次。
int bitSum(int n) // 返回 n 这个数每⼀位上的平⽅和{int sum = 0;while(n){int t = n % 10;sum += t * t;n /= 10;}return sum;}bool isHappy(int n) {int slow = n, fast = bitSum(n);while(slow != fast){slow = bitSum(slow);fast = bitSum(bitSum(fast));}return slow == 1;}
还有一种写法就是让他们一直循环，指定一个比较大的数作为循环次数，在循环过程中如果出现1，那就返回true，如果一直没有，那就返回false。
class Solution {
public:int key(int x){int num=0;while(x>0){int a=x%10;x=x/10;num+=pow(a,2);}return num;}bool isHappy(int n) {int k=7;while(k>0){n=key(n);if(n==1){return true;}k--;}return false;}
};
这里尝试了一下，其实循环7次就可以判断出所有的测试用例。虽然有点不严谨，但能过就成。
有效三角形的个数
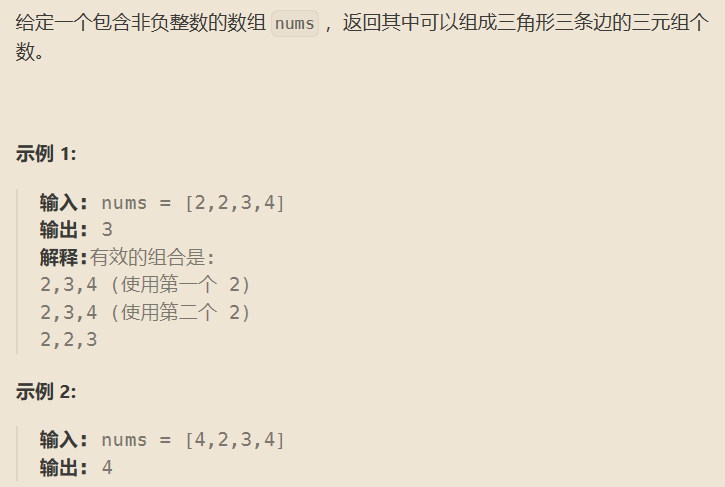
首先，我们都知道，给你三条边，构成三角形的条件是小的那两条边的和大于大的那条边，局可以验证是否为三角形。
暴力求解的思路：
所定一个数字，依次遍历其他数字，这种写法的话时间复杂度为n3。
得到三个数，在进行判断就好了。
知道
优化解法
既然要知道最大的数，我们就可以先对数组进行排序，然后再进行判断，从后往前指定最大的数，判断这个数为最大边长的数会产生几个三角形，判断完成之后向前移位，在判断倒数第二大得数作为最大边长会产生几个三角形。
在前边遍历时，如何进行遍历呢？
如下动图展现
这种写法，在指定end要进行n次循环，遍历时使用双指针思想，只进行一次循环，所以优化后的代码只需要O(N2)不到即可解决问题。
当然还可以进行优化，直接将second放在判断位置即（end）前，如果first和second上的两个数判断不成立，那就直接++left，直到确定是三角形，此时right-left的值就是right作为第二条边时可以产生的三角形数目，因为left前边的数大于等于left，一定符合条件。
然后second–，继续判断，直到first和second会和，再将end向前移动。
代码实现：
class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int end=nums.size()-1;int count=0;for(int i=end;i>1;i--){int left=0;int right=i-1;while(left<right){if(nums[left]+nums[right]>nums[i]){count+=right-left;right--;}else{left++;}}}return count;}
};
下一篇文章我会给大家带来三数之和，四叔之后的讲解，有收获的话留下你的赞吧！有问题请赐教，我会虚心改正。
