统计学-R语言-4.7

文章目录

前言
描述水平的统计量
- 平均数
- 分位数
- - 中位数
  - 四分位数
- 众数
- 描述差异的统计量（数据离散程度）
- - 极差
  - 四分位差
  - 方差和标准差
  - 变异系数
  - 标准分数
描述分布形状的统计量
- 偏度与偏度系数
- 峰度与峰度系数
数据的综合描述
- 综合描述的R函数
- 综合描述的实例
总结

前言

本篇文章将介绍数据的描述统计量。

描述水平的统计量

平均数

平均数也称为均值，常用的统计量之一
消除了观测值的随机波动
易受极端值的影响
根据总体数据计算的，称为总体平均数，记为；根据样本数据计算的，称为样本平均数，记为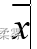在这里插入图片描述。
设一组数据为：x1 ，x2 ，… ，xn (总体数据xN) 。

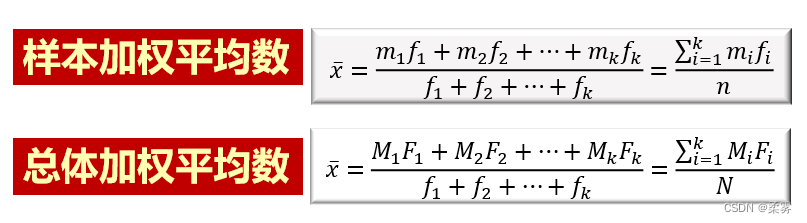
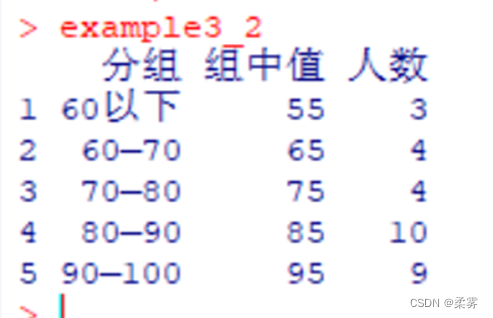
计算30名学生考试分数的加权平均数

 load("C:/example/ch3/example3_2.RData")weighted.mean (example3_2$组中值,example3_2$人数)#example3_2$人数权数向量

在这里插入图片描述

分位数

中位数

排序后处于中间位置上的值。不受极端值影响。

在这里插入图片描述

四分位数

用3个点等分数据。排序后处于25%和75%位置上的值。
在这里插入图片描述
30名学生的考试分数的中位数。(example3_1)

load("C:/example/ch3/example3_1.RData")
median(example3_1$分数)

计算30名学生考试分数的四分位数。(example3_1)

load("C:/example/ch3/example3_1.RData")
quantile(example3_1$分数,probs=c(0.25,0.75),type=6)

用R计算汇总输出基本的描述统计量。(example3_1)

load("C:/example/ch3/example3_1.RData")
summary(example3_1$分数)  # 默认使用type=7

众数

一组数据中出现次数最多的变量值；
适合于数据量较多时使用；
不受极端值的影响；
一组数据可能没有众数或有几个众数。

编写函数计算众数(example3_1)

load("C:/example/ch3/example3_1.RData")
mode<-function(x){
ux<-sort(unique(x))   # 列出每一个的数值并排序，unique主要是返回一个把重复元素或行给删除的向量、数据框或数组
tab<-tabulate(match(x,ux))      # 比较x与ux中相同的数值，列出它们在ux中位置，再计算每个位置的频数ux[tab==max(tab)]              # 找出ux对象中频数最多的元素}
mode(example3_1$分数)           # 使用mode函数计算对象的众数

which.max函数 —无众数返回1，双众数只返回第一个。

load("C:/example/ch3/example3_1.RData")	
which.max(table(example3_1$分数))
14     #众数在频数分布表的第14位

描述差异的统计量（数据离散程度）

极差

一组数据的最大值与最小值之差
离散程度的最简单测度值
易受极端值影响
未考虑数据的分布
计算公式为：
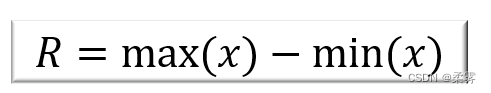
在这里插入图片描述

load("C:/example/ch3/example3_1.RData")
R<-max(example3_1$分数)-min(example3_1$分数)
R
# 或写为：
R<-diff(range(example3_1$分数))
R

四分位差

也称四分位距。上四分位数与下四分位数之差
反映了中间50%数据的离散程度
不受极端值的影响
用于衡量中位数的代表性
R函数：

IQR(example3_1$分数,type=6)

在这里插入图片描述

计算30名学生考试分数极差和四分位差
计算极差

load("C:/example/ch3/example3_1.RData")
range<-max(example3_1$分数)-min(example3_1$分数)
range

计算四分位差

IQR(example3_1$分数,type=6)

方差和标准差

数据离散程度的最常用测度值
反映各变量值与均值的平均差异
根据总体数据计算的，称为总体方差(标准差)，记为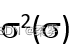在这里插入图片描述
；根据样本数据计算的，称为样本方差(标准差)，记为s2(s)。

在这里插入图片描述

计算30名学生考试分数的方差和标准差。
方差

load("C:/example/ch3/example3_1.RData")
var(example3_1$分数)

标准差

sd(example3_1$分数)

变异系数

标准差与其相应的均值之比
对数据相对离散程度的测度
消除了数据水平高低和计量单位的影响，其数值越大，说明数据的相对离散程度也就越大。
用于对不同组别数据离散程度的比较，计算公式为：
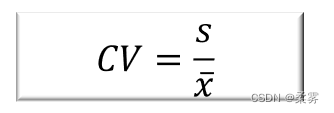
在这里插入图片描述
(数据: example3_9. RData)在奥运会女子10米气手枪比赛中,每个运动员首先进行每组10枪共4组的预赛,然后根据预赛总成绩确定进入决赛的8名运动员。决赛时8名运动员进行10枪射击,再将预赛成绩加上决赛成绩确定最后的名次。在2008年8月10日举行的第29届北京奥运会女子10米气手枪决赛中,进入决赛的8名运动员最后10枪的决赛成绩如下表所示。计算平均数、标准差和变异系数,评价运动员的射击水平及发挥的稳定性,并结合箱线图进行分析。
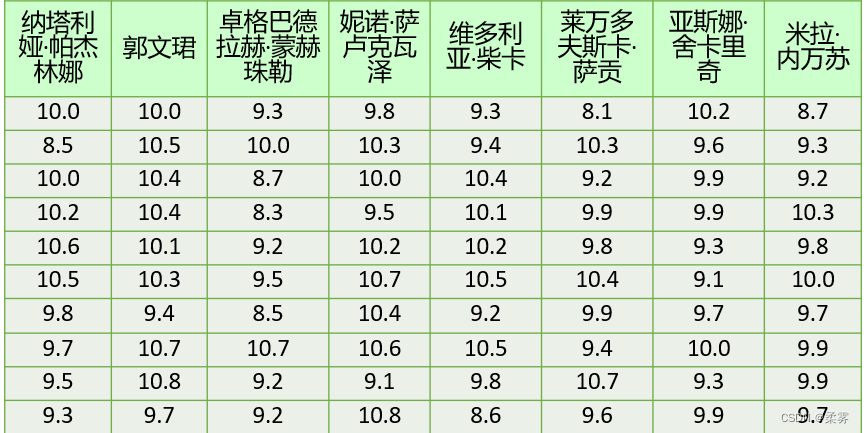
在这里插入图片描述
如果各运动员决赛的平均成绩差异不大，可以直接比较标准差的大小，否则需要计算变异系数。R代码和结果如下所示：

load("C:/example/ch3/example3_9.RData")
mean<-apply(example3_9,2,mean)#apply()函数把一个function作用到数据对象中的每一行或者每一列中，简单的说，apply函数经常用来计算矩阵中行或列的均值、标准差、方差的函数
sd<-apply(example3_9,2,sd)
cv<-sd/mean
x<-data.frame("平均环数"=mean,"标准差"=sd,"变异系数"=cv)
round(x,4)

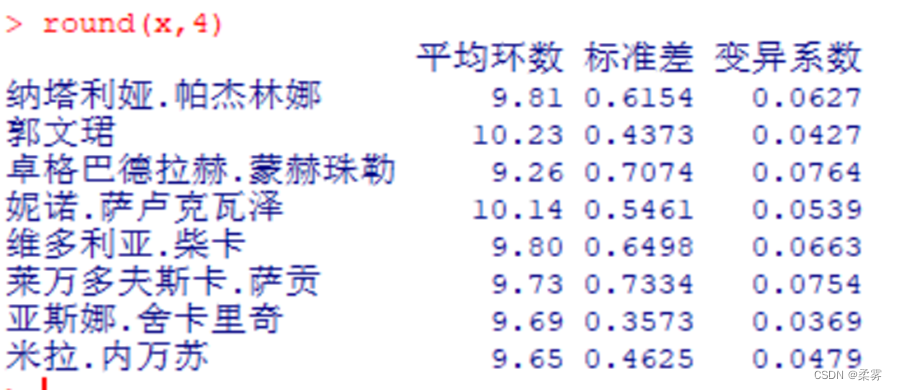
在这里插入图片描述

par(cex=.6,mai=c(.7,.7,.1,.1))
boxplot(example3_9,notch=TRUE,col="lightblue",ylab="射击环数", xlab="运动员")

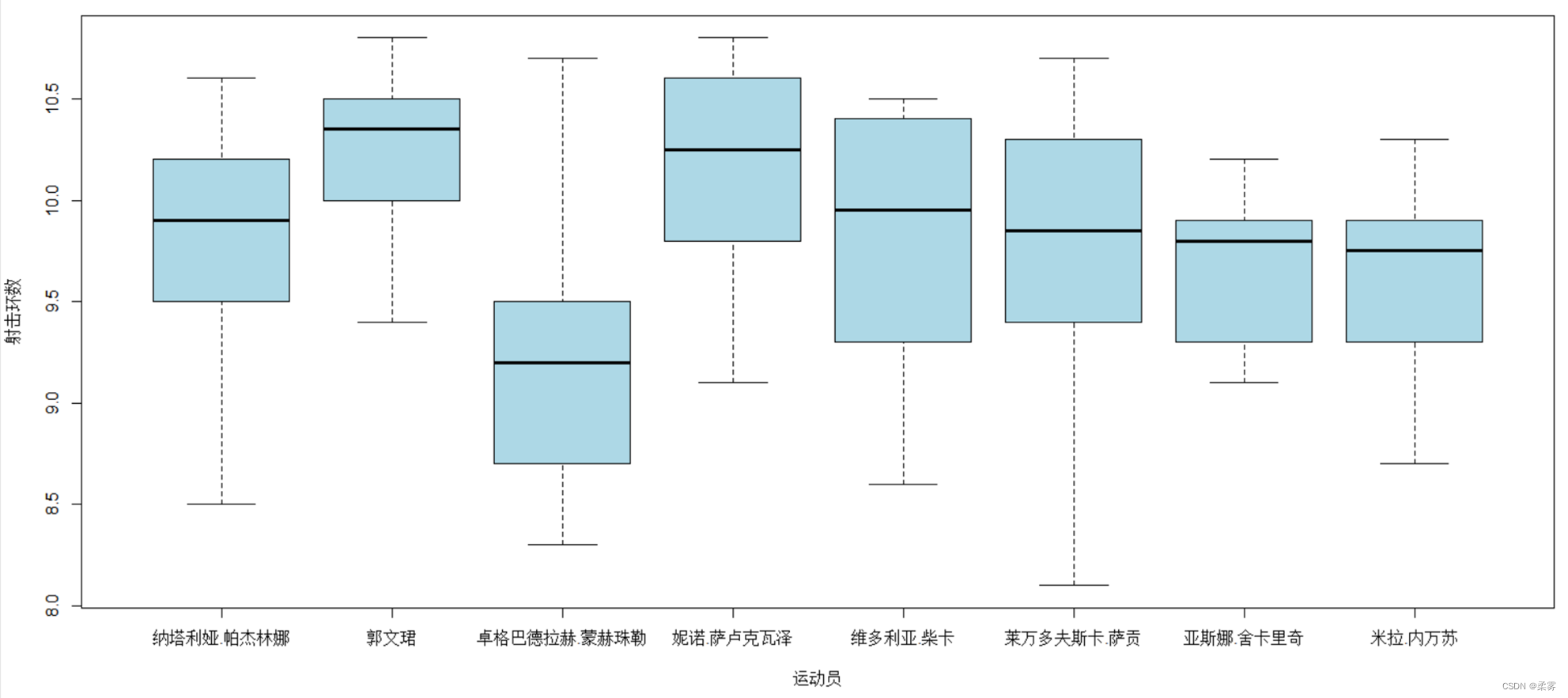
在这里插入图片描述
从变异系数可以看出，在最后10枪的决赛中，发挥比较稳定的运动员是塞尔维亚的亚斯娜·舍卡里奇（变异系数为0.0369）和中国的郭文珺（变异系数为0.0427），发挥不稳定的运动员是蒙古国的卓格巴德拉赫·蒙赫珠勒（变异系数为0.0764）和波兰的莱万多夫斯卡·萨贡（变异系数为0.0754）。由于郭文珺的平均环数远高于其他选手，可以很好地佐证上述结论且发挥稳定，最终获得了本届奥运会女子10米气手枪决赛的金牌。箱线图也可以很好地佐证上述结论。

标准分数

对某一个值在一组数据中相对位置的度量。也称标准化值
可用于判断一组数据是否有离群点(outlier)
比如，全班的平均考试分数为80分，标准差为10分，如果一个学生的考试分数是90分，表示距离平均分数有1个标准差的距离。这里的1就是这个学生考试成绩的标准分数。标准分数描述的是某个数据与平均数相比相差多少个标准差，它是某个数据与其平均数的差除以标准差后的数值。设标准分数为z，
计算公式为
在这里插入图片描述

数据：example3_1.RData）沿用例3—1。计算30名学生考试分数的标准分数

load("C:/example/ch3/example3_1.RData")
as.vector(round(scale(example3_1$分数),4))

在这里插入图片描述
注：函数scale（x，）用于计算标准分数，x为向量或矩阵。as. vector（x）函数将结果以向量形式输出，round（x）函数将结果保留4位小数。
思考：为什么标准分数能判断一组数据是否有离群点？
第一个学生的标准分数为0.3784，表示这个学生的考试分数与平均分数（80分）相比高出0.3784个标准差；第二个学生的标准分数为-1.8919，表示其考试分数与平均分数相比低1.8919个标准差。其余的含义类似。
根据标准分数可以判断一组数据中是否存在离群点。经验表明：当一组数据对称分布时，约有68%的数据在平均数加减1个标准差的范围之内，约有95%的数据在平均数加减2个标准差的范围之内，约有99%的数据在平均数加减3个标准差的范围之内。可以想象，一组数据中低于或高于平均数3倍标准差之外的数值是很少的，因此通常将3个标准差之外的数据确定为离群点。
经验法则表明：当一组数据对称分布时
约有68%的数据在平均数加减1个标准差的范围之内
约有95%的数据在平均数加减2个标准差的范围之内
约有99%的数据在平均数加减3个标准差的范围之内

描述分布形状的统计量

偏度与偏度系数

K.Pearson于1895年首次提出。指数据分布的不对称性
测度统计量是偏度系数(coefficient of skewness SK)
𝑆𝐾=𝟎为对称分布；𝑆𝐾>𝟎为右偏分布；𝑆𝐾<𝟎为左偏分布
𝑆𝐾大于1或小于−1，为高度偏度分布； 𝑆𝐾在0.5～1或−1～−0.5之间，为是中等偏度分布； 𝑆𝐾越接近0，偏斜程度就越低。
计算公式
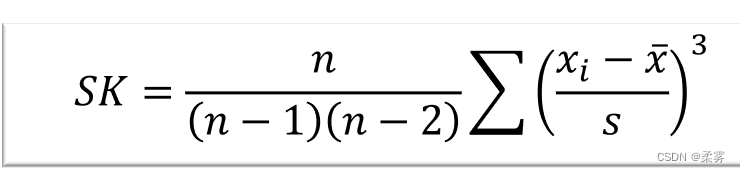
在这里插入图片描述

峰度与峰度系数

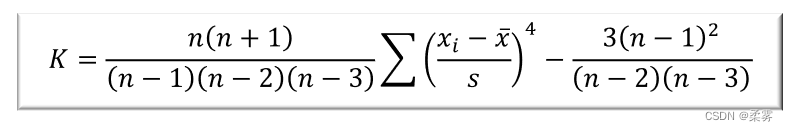
在这里插入图片描述

不同分布的偏度系数和峰度系数。

来自不同分布的模拟数据，样本量=5000
library(e1071) # 加载“skewness”和“kurtosis”函数包
par(mfrow=c(1,3),mai=c(0.7,0.5,0.2,0.1))
mf<-function(x){
hist(x,probability=T,col='lightblue',xlab="x",ylab="Density",
sub=paste("skewness=",round(skewness(x),digits=4)),#paste函数将他的参数转换为字符串并连接他们
main=paste("kurtosis=",round(kurtosis(x),digits=4)))
lines(density(x),col='red',lwd=2)
}
n<-5000
mf(rchisq(n,10))#咖方分布
mf(rnorm(n))
mf(-rchisq(n,10)+36)
#注：每次运行上述代码都会得到略有不同的分布形状和偏度系数及峰度系数，可以反复进行模拟

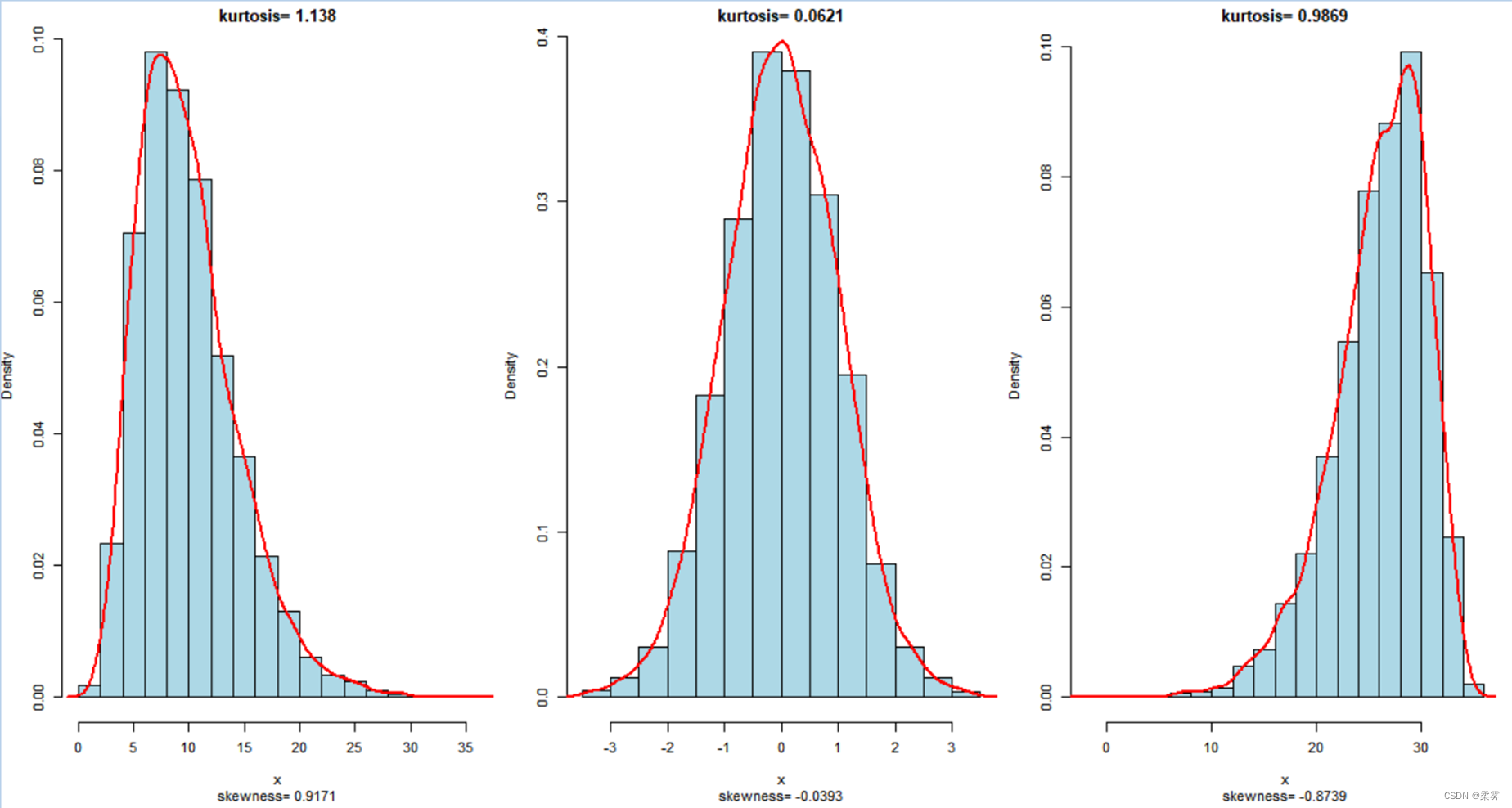
在这里插入图片描述
沿用例3-1。计算30名学生考试分数的偏度系数和峰度系数
计算偏度系数

library(agricolae) 
skewness(example3_1$分数)

计算峰度系数

kurtosis(example3_1$分数)

偏度系数和峰度系数有不同的计算方法，R的e1071包中提供了各种方法的介绍，type=2与上述结果相同。
结果显示，30名学生考试分数的偏度系数为-0.8313613，表示考试分数的分布为左偏分布，且偏斜程度较大。峰度系数为-0.3514637，说明考试分数分布的峰值比标准正态分布的峰值要略低一些。

数据的综合描述

综合描述的R函数

绘制使用pastecs包中的stat.desc()函数计算描述统计量

load("C:/example/ch3/example3_9.RData")
library(pastecs)
round(stat.desc(example3_9),4)

使用psych包中的describe()函数计算描述统计量

library(psych)
describe(example3_9)

综合描述的实例

在实际分析中，通常要对数据从图表和统计量两个方面同时进行描述。通过如下实例来说明对数据进行综合描述的基本思路：
60个大学生的调查数据(部分)（example3_12）
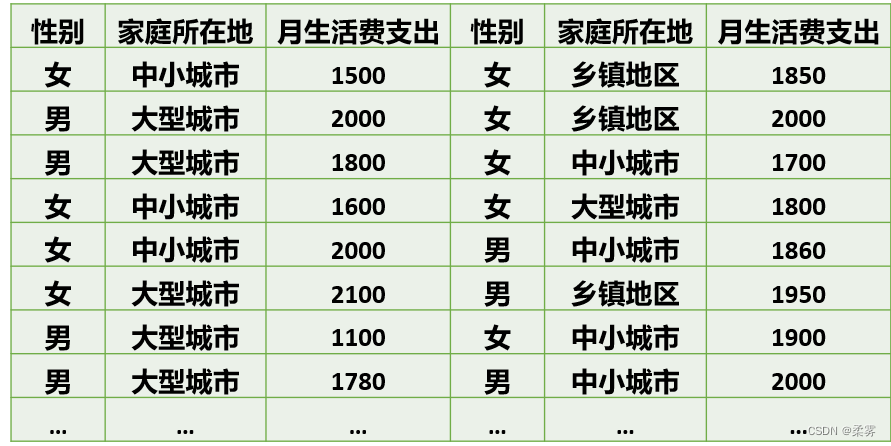
在这里插入图片描述
提示：这里涉及两个类别变量和一个数值变量。对于性别和家庭所在地两个类别变量，可以对其频数进行计数，计算百分比，并画出条形图和饼图等进行描述。对于月生活费支出变量，可以绘制直方图、茎叶图、箱线图等来观察其分布特征，并计算均值和标准差等统计量进行分析。
首先，对性别和家庭所在地两个类别变量统计频数，观察各自的分布状况。
使用summary函数对类别数据计数和对数值数据计算描述统计量(example3_12)

summary(example3_12)

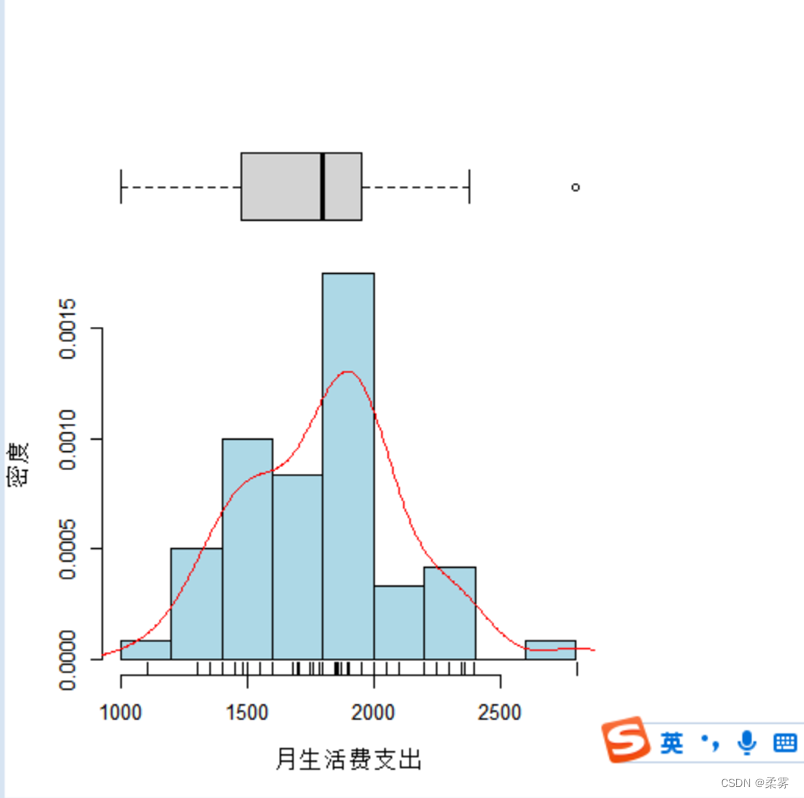
在这里插入图片描述
其次，对月生活费支出做整体描述。画出60个学生月生活费支出的直方图、茎叶图和箱线图，观察月生活费支出的分布状况。
绘制带有箱线图、轴须线和密度估计的直方图

load("C:/example/ch3/example3_12.RData")
attach(example3_12)
par(fig=c(0,0.8,0,0.8),cex=0.8)
hist(月生活费支出,xlab="月生活费支出",ylab="密度",freq =FALSE,col="lightblue",main="")
rug(jitter(月生活费支出))
lines(density(月生活费支出),col="red")
par(fig=c(0,0.8,0.35,1),new=TRUE)
boxplot(月生活费支出,horizontal=TRUE,axes=FALSE)
par(fig=c(0,0.8,0.5,1),new=TRUE)
boxplot(月生活费支出,horizontal=TRUE,axes=FALSE)

在这里插入图片描述
绘制茎叶图

library(aplpack)

library(aplpack)
stem.leaf(example3_12$月生活费支出)

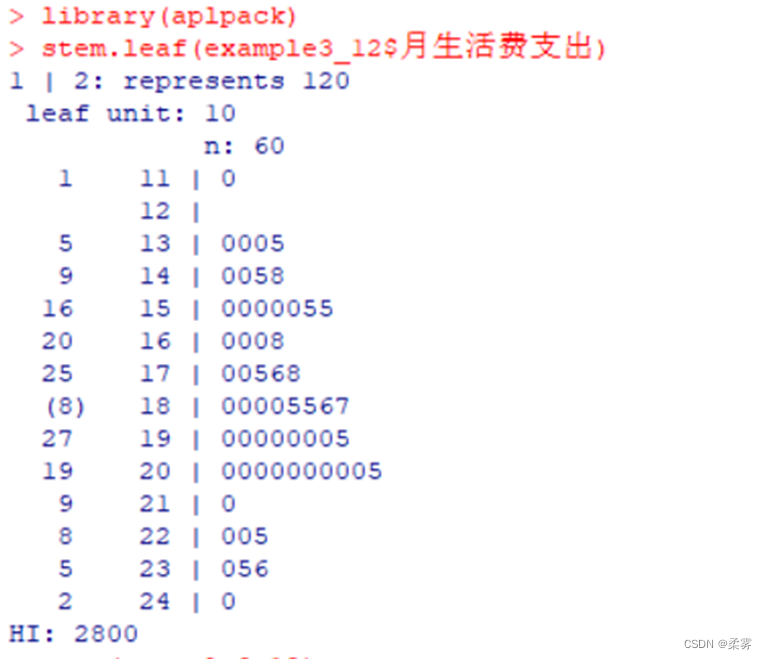
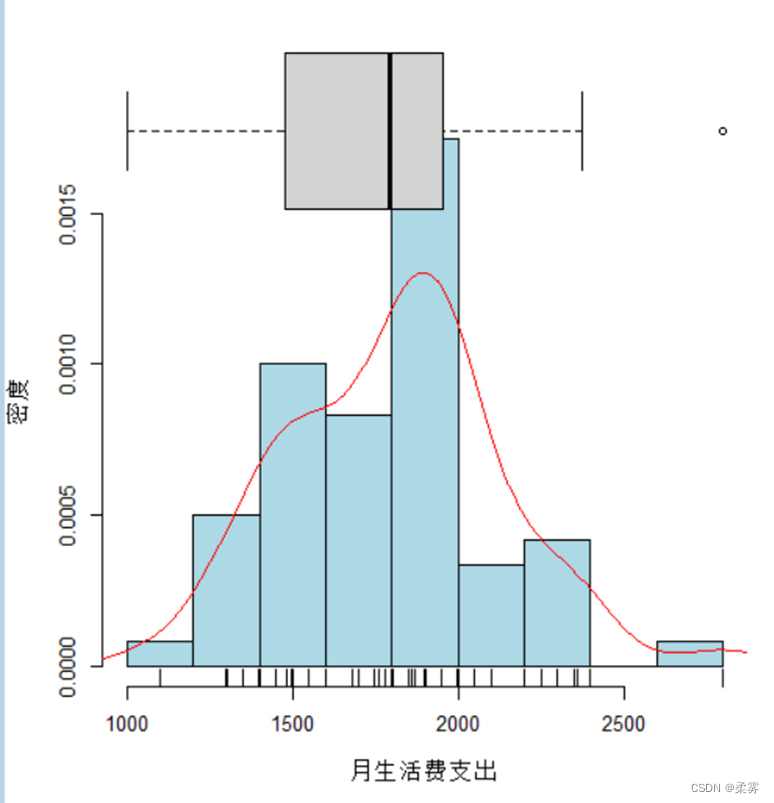
在这里插入图片描述

从图中可以看出，大学生月生活费支出的分布基本上是对称的，也就是以均值为中心，两侧依次减少，这基本上符合大学生生活费支出的特点。

再次，分别按性别和家庭所在地进行分类描述。分析不同性别和不同家庭所在地的学生月生活费支出的特征，看看性别和家庭所在地对生活费支出是否有影响.分别按性别和家庭所在地分类计算描述统计量的R代码和结果如下所示

my_summary<-function(x){library(agricolae) with(x,data.frame(N=length(月生活费支出),"平均数"=mean(月生活费支出),"中位数"=median(月生活费支出),"标准差"=sd(月生活费支出),
"全距"=max(月生活费支出)-min(月生活费支出),
"变异系数"=sd(月生活费支出)/mean(月生活费支出),"偏度系数"=skewness(月生活费支出)))
}library(plyr)ddply(example3_12,.(性别),my_summary)ddply(example3_12,.(家庭所在地),my_summary)

    注：首先编写了包含关心的统计量的汇总函数。plyr包中的ddply函数可以对数据分组应用统计函数，函数 ddply（data， .variables，fun，）中的data为数据集， .variables指对哪个变量分组，fun为应用的统计函数。

在这里插入图片描述
结果显示，女生月生活费支出的平均数和中位数均高于男生，同时女生生活费支出的标准差和全距也都大于男生，相应的变异系数CV女=0.1750539>CV男=0.1619382，说明女生生活费支出的离散程度大于男生。从分布形态看，女生生活费支出的偏度系数是0.5028245，为右偏分布，而男生生活费支出的偏度系数是-0.5485891，为左偏分布。

在这里插入图片描述
此外，还可以同时按性别和家庭所在地分类描述其月生活费支出，也就是按性别分类的同时再按家庭所在地分类，然后计算各自的描述统计量，如均值、中位数、标准差、变异系数、极差、偏度系数等。
同时按性别和家庭所在地分类描述

library(reshape)
library(agricolae)
mystats<-function(x)
{c(n=length(x),mean=mean(x),median=median(x),sd=sd(x),CV=sd(x)/mean(x),R=(max(x)-min(x)),SK=skewness(x))}dfm<- melt(example3_12,measure.vars="月生活费支出",id.vars=c("性别","家庭所在地"))
cast(dfm,性别+家庭所在地+variable~., mystats)

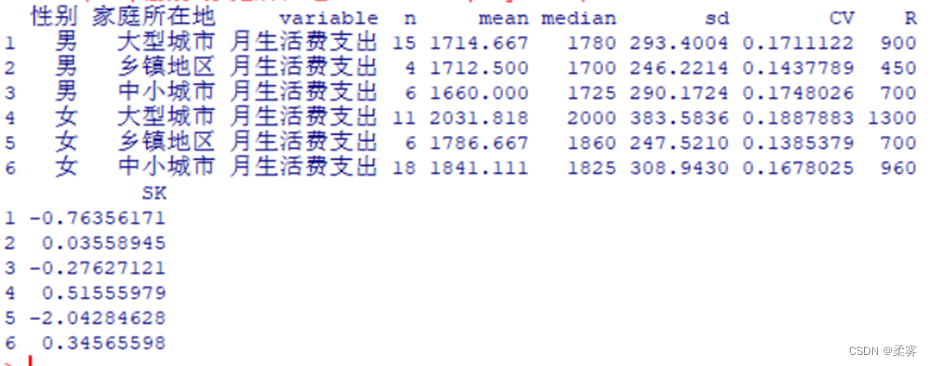
在这里插入图片描述
1.mystats为自编函数，计算所需的统计量；melt为融合数据，指明要描述的数值变量和类别变量；cast重新构建输出结果的数据框。
2.安装doBy包，使用 summaryBy（月生活费支出~性别+家庭所在地，data=example3_12，FUN= mystats）可以得到类似的结果。

为比较不同性别和不同家庭所在地的学生月生活费支出的分布状况，还可以按类别分别绘制点图和箱线图（也可以绘制直方图）。
按性别和家庭所在地分类绘制点图

library(lattice)
stripplot(月生活费支出~家庭所在地+性别,col=c("red","blue"),pch=c(19,8),cex=0.7)

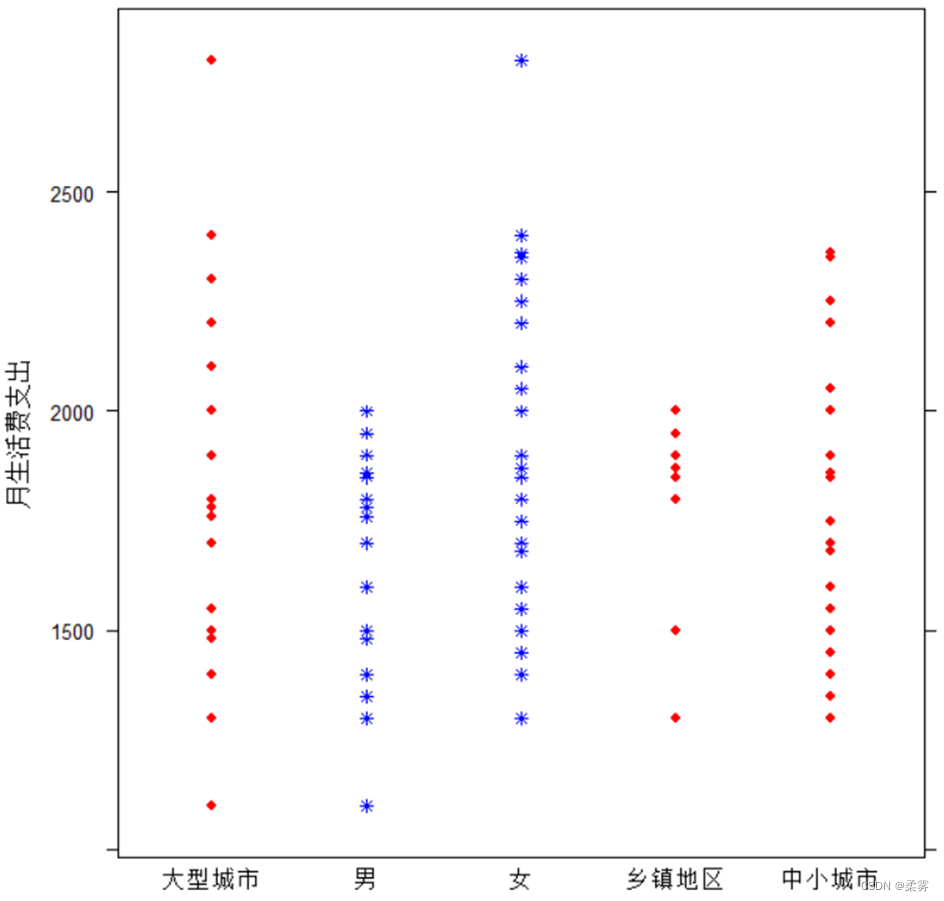
在这里插入图片描述
图显示，女生支出的平均水平明显高于男生；大城市和中小城市的平均支出水平差异不大，乡镇地区的平均支出水平偏低。

按性别和家庭所在地分类绘制箱线图

boxplot(月生活费支出~家庭所在地*性别,col=c(2:4),ylab="月生活费支出")

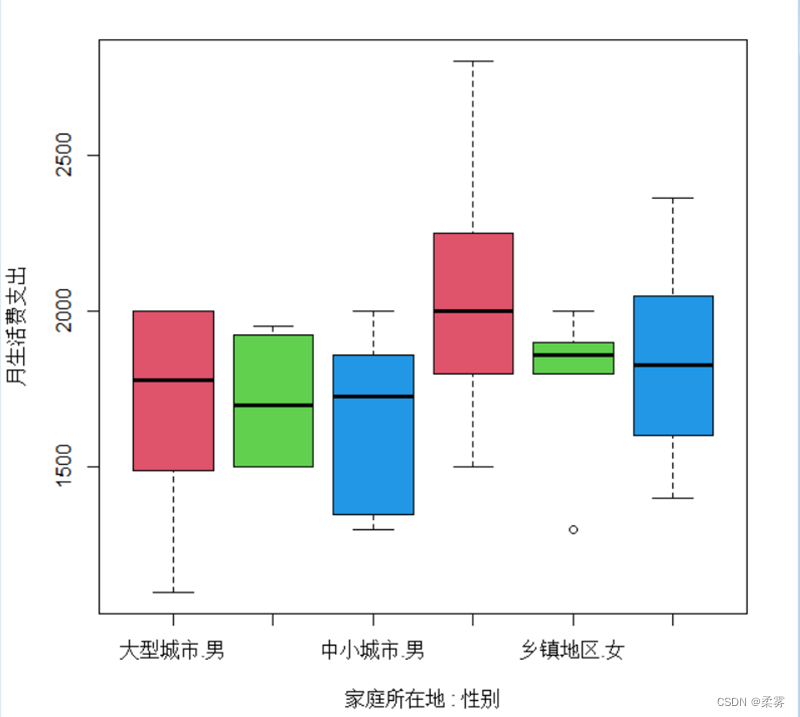
在这里插入图片描述

图显示，大城市女生支出的平均水平明显高于中小城市和乡镇地区，该图还可以用于比较按性别和按家庭所在地分类的学生月生活费支出分布的特点。

总结

本篇是对数据描述的统计量进行的最后一个篇章的介绍，有部分的例题作为介绍，希望对大家的学习有所帮助。