【React源码 - Diff算法】

介绍

在React学习中，Diff算法(协调算法)，想必我们并不陌生，简单来说就是一个对比新老节点寻找差异，然后找出最小的一个变化集，最后对这个最小变化集进行最小的DOM操作，本文将从源码来分析在React(17.0.2)中是如何来通过这个算法来进行对比并让Renderer知道如果操作DOM的。

在reconcileChildFibers中，主要是通过newChild的类型以及type来判断执行那个函数来更新fiber，其中主要类型分为非空对象、字符串/数字、数组、可迭代类型。
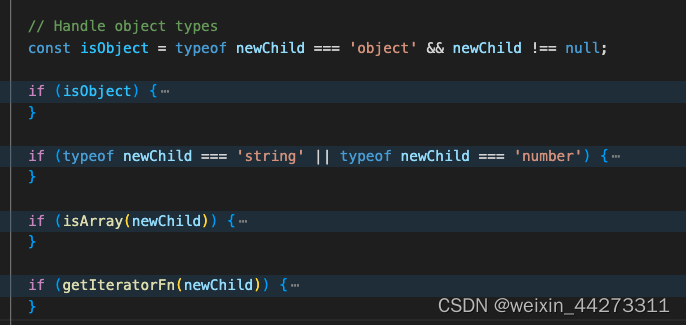
在这里插入图片描述
其中我们主要对非空对象的React Element(reconcileSingleElement函数)以及数组(reconcileChildrenArray函数，可迭代reconcileChildrenIterator和该函数核心逻辑大致一样)的处理来分析DIff算法：

if (isObject) {switch (newChild.$$typeof) {case REACT_ELEMENT_TYPE:return placeSingleChild(reconcileSingleElement(returnFiber,currentFirstChild,newChild,lanes,),);case REACT_PORTAL_TYPE:return placeSingleChild(reconcileSinglePortal(returnFiber,currentFirstChild,newChild,lanes,),);case REACT_LAZY_TYPE:if (enableLazyElements) {const payload = newChild._payload;const init = newChild._init;// TODO: This function is supposed to be non-recursive.return reconcileChildFibers(returnFiber,currentFirstChild,init(payload),lanes,);}}}

if (isArray(newChild)) {return reconcileChildrenArray(returnFiber,currentFirstChild,newChild,lanes,);}

DIff算法可以分为两种：

  • 单节点对比(reconcileSingleElement)
  • 多节点对比(reconcileChildrenArray)

单节点对比

我们从reconcileSingleElement函数来分析，当虚拟DOM为一个非空对象时，React是如何进行单节点对比的：

function reconcileSingleElement(returnFiber: Fiber,currentFirstChild: Fiber | null,element: ReactElement
): Fiber {const key = element.key;let child = currentFirstChild;// 首先判断是否存在对应DOM节点while (child !== null) {// 上一次更新存在DOM节点，接下来判断是否可复用// 首先比较key是否相同if (child.key === key) {// key相同，接下来比较type是否相同switch (child.tag) {// ...省略casedefault: {if (child.elementType === element.type) {// 将该fiber及其兄弟fiber标记为删除deleteRemainingChildren(returnFiber, child.sibling);// type相同则表示可以复用const existing = useFiber(child, element.props);// 更新复用节点的refexisting.ref = coerceRef(returnFiber, child, element);existing.return = returnFiber;// 返回复用的fiberreturn existing;}// type不同则跳出switchbreak;}}// 代码执行到这里代表：key相同但是type不同// 将该fiber及其兄弟fiber标记为删除deleteRemainingChildren(returnFiber, child);break;} else {// key不同，将该fiber标记为删除deleteChild(returnFiber, child);}child = child.sibling;}// 创建新Fiber，并返回 ...省略
}

从代码中能看出，先判断当前fiber是否有对应的dom节点，如果是新增节点（child === null）, 直接新建 fiber, 没有多余的逻辑。如果是对比更新，如果key不一样则给当前fiber打上delete的标记，继续遍历兄弟节点，key一样type不一样则给当前fiber和其兄弟节点都打上delete标记，key和type都相同(即: ReactElement.key === Fiber.key 且 Fiber.elementType === ReactElement.type), 则复用useFiber，并更新ref，否则新建。

注意: 复用过程是调用useFiber(child, element.props)创建新的fiber对象, 这个新fiber对象.stateNode = currentFirstChild.stateNode, 即stateNode属性得到了复用, 故 DOM 节点得到了复用.因为stateNode保存的就是DOM节点信息.所以常说的复用节点可以简单粗暴的理解为复用stateNode属性

当key相同且type不同时，代表我们已经根据key找到本次更新组件，但是组件发生了更新，不能复用。既key的唯一可能性已经不能复用，则剩下的fiber都没有继续查找的必要，所以都需要标记删除。
当key不同时只代表遍历到的该fiber不能被复用，后面还有兄弟fiber还没有遍历到。所以仅仅标记该fiber删除。

代码流程可以简述为：
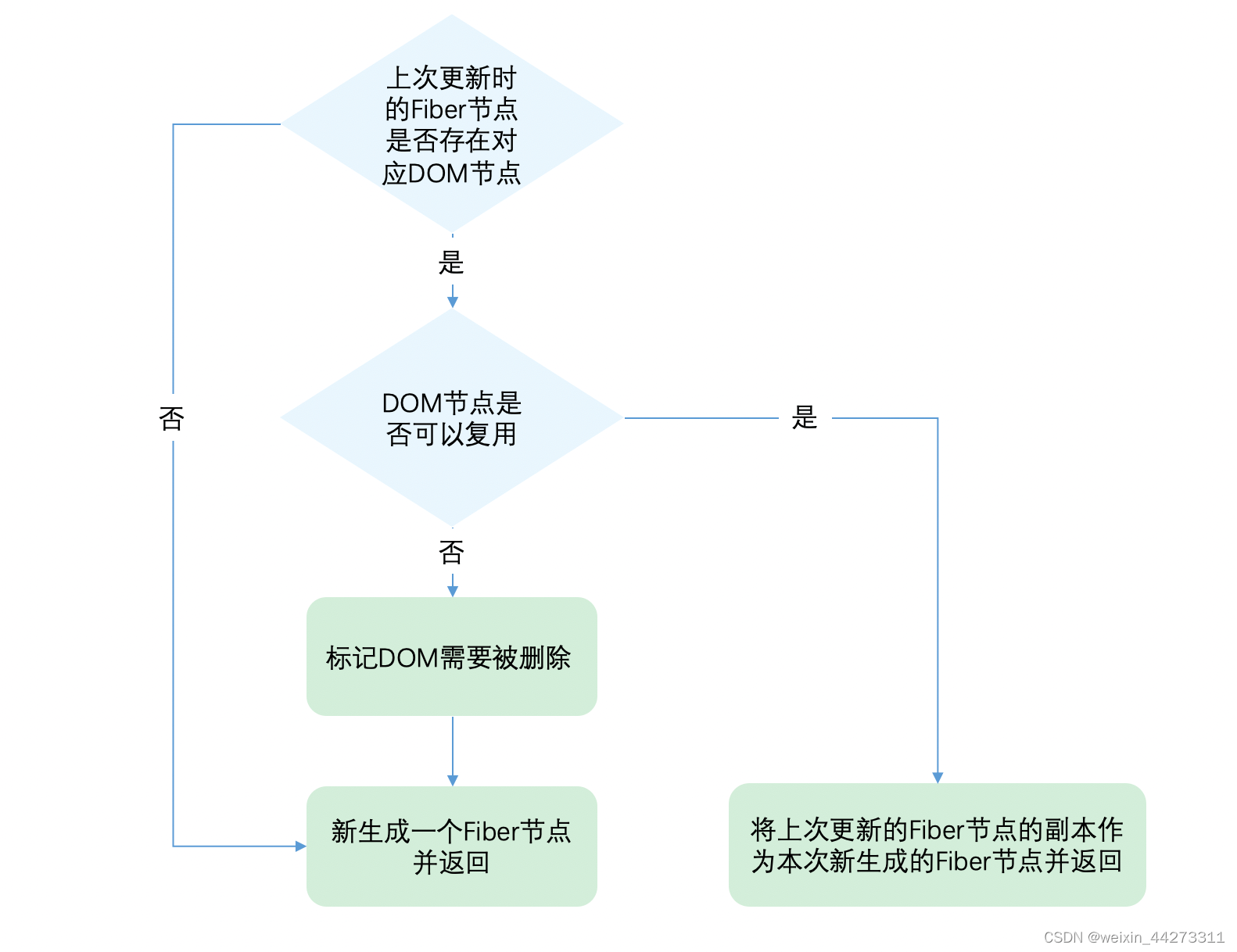
在这里插入图片描述

多节点对比

这里我们通过reconcileChildrenArray来分析React中对于多节点是如何进行对比复用的。

// reconcileChildFibers函数中
if (isArray(newChild)) {return reconcileChildrenArray(returnFiber,currentFirstChild,newChild,lanes,);}

通过isArray判断是否是数组，如果是则进行多节点Diff对比，会进行两次遍历，

function reconcileChildrenArray(returnFiber: Fiber,currentFirstChild: Fiber | null,newChildren: Array<*>,lanes: Lanes,
): Fiber | null {let resultingFirstChild: Fiber | null = null;let previousNewFiber: Fiber | null = null;let oldFiber = currentFirstChild;let lastPlacedIndex = 0;let newIdx = 0;let nextOldFiber = null;// 1. 第一次循环: 遍历最长公共序列(key相同), 公共序列的节点都视为可复用for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {// 后文分析}if (newIdx === newChildren.length) {// 如果newChildren序列被遍历完, 那么oldFiber序列中剩余节点都视为删除(打上Deletion标记)deleteRemainingChildren(returnFiber, oldFiber);return resultingFirstChild;}if (oldFiber === null) {// 如果oldFiber序列被遍历完, 那么newChildren序列中剩余节点都视为新增(打上Placement标记)for (; newIdx < newChildren.length; newIdx++) {// 后文分析}return resultingFirstChild;}// ==================分割线==================const existingChildren = mapRemainingChildren(returnFiber, oldFiber);// 2. 第二次循环: 遍历剩余非公共序列, 优先复用oldFiber序列中的节点for (; newIdx < newChildren.length; newIdx++) {}if (shouldTrackSideEffects) {// newChildren已经遍历完, 那么oldFiber序列中剩余节点都视为删除(打上Deletion标记)existingChildren.forEach((child) => deleteChild(returnFiber, child));}return resultingFirstChild;
}

所谓的新老节点对比，在这里就是currentFirstChild和newChildren两个序列的对比：

  • currentFirstChild: 是一个fiber节点, 通过fiber.sibling可以将兄弟节点全部遍历出来. 所以可以将currentFirstChild理解为链表头部, 它代表一个序列, 源码中被记为oldFiber.
  • newChildren: 是一个数组, 其中包含了若干个ReactElement对象. 所以newChildren也代表一个序列.

所以reconcileChildrenArray实际就是 2 个序列之间的比较(链表oldFiber和数组newChildren), 最后返回合理的fiber序列.
上述代码中, 以注释分割线为界限, 整个核心逻辑分为 2 步骤:

  • 第一次循环: 遍历最长公共序列(key 相同), 公共序列的节点都视为可复用
    如果newChildren序列被遍历完, 那么oldFiber序列中剩余节点都视为删除(打上Deletion标记)
    如果oldFiber序列被遍历完, 那么newChildren序列中剩余节点都视为新增(打上Placement标记)
  • 第二次循环: 遍历剩余非公共序列, 优先复用 oldFiber 序列中的节点，以[key, oldFiber]的形式Map结构存储，方便快速查找复用节点
    在对比更新阶段(非初次创建fiber, 此时shouldTrackSideEffects被设置为 true). 第二次循环遍历完成之后, oldFiber序列中没有匹配上的节点都视为删除(打上Deletion标记)

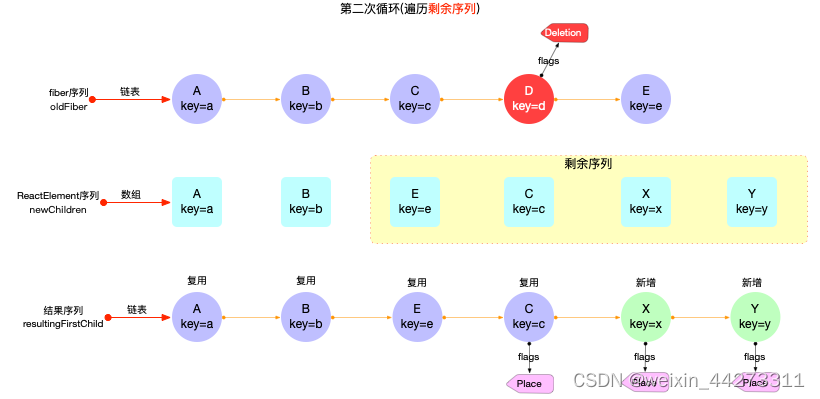
假设有如下图所示 2 个初始化序列:

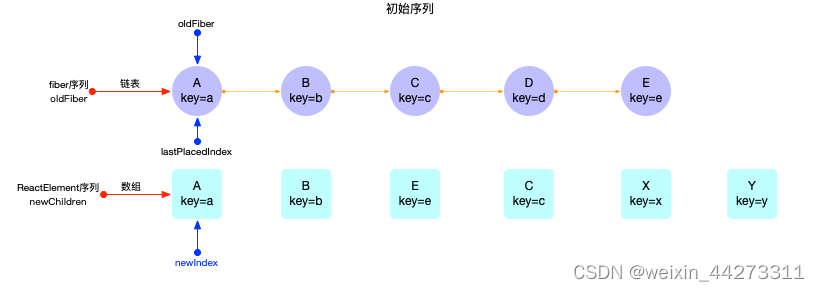
在这里插入图片描述
接下来第一次循环, 会遍历公共序列A,B, 生成的 fiber 节点fiber(A), fiber(B)可以复用.
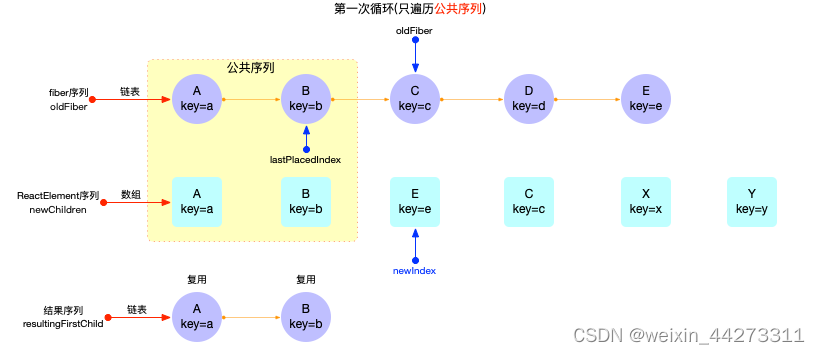
在这里插入图片描述
最后第二次循环, 会遍历剩余序列E,C,X,Y:

  • 生成的 fiber 节点fiber(E), fiber©可以复用. 其中fiber©节点发生了位移(打上Placement标记).
  • fiber(X), fiber(Y)是新增(打上Placement标记).
  • 同时oldFiber序列中的fiber(D)节点确定被删除(打上Deletion标记).
    在这里插入图片描述
    整个主干逻辑就介绍完了, 接下来贴上完整源码

第一次循环：

// 1. 第一次循环: 遍历最长公共序列(key相同), 公共序列的节点都视为可复用
for (; oldFiber !== null && newIdx < newChildren.length; newIdx++) {if (oldFiber.index > newIdx) {nextOldFiber = oldFiber;oldFiber = null;} else {nextOldFiber = oldFiber.sibling;}// new槽位和old槽位进行比较, 如果key不同, 返回null// key相同, 比较type是否一致. type一致则执行useFiber(update逻辑), type不一致则运行createXXX(insert逻辑)const newFiber = updateSlot(returnFiber,oldFiber,newChildren[newIdx],lanes,);if (newFiber === null) {// 如果返回null, 表明key不同. 无法满足公共序列条件, 退出循环if (oldFiber === null) {oldFiber = nextOldFiber;}break;}if (shouldTrackSideEffects) {// 若是新增节点, 则给老节点打上Deletion标记if (oldFiber && newFiber.alternate === null) {deleteChild(returnFiber, oldFiber);}}// lastPlacedIndex 记录被移动的节点索引// 如果当前节点可复用, 则要判断位置是否移动.lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);// 更新resultingFirstChild结果序列if (previousNewFiber === null) {resultingFirstChild = newFiber;} else {previousNewFiber.sibling = newFiber;}previousNewFiber = newFiber;oldFiber = nextOldFiber;
}

第二次循环：

// 1. 将第一次循环后, oldFiber剩余序列加入到一个map中. 目的是为了第二次循环能顺利的找到可复用节点
const existingChildren = mapRemainingChildren(returnFiber, oldFiber);// 2. 第二次循环: 遍历剩余非公共序列, 优先复用oldFiber序列中的节点
for (; newIdx < newChildren.length; newIdx++) {// [key, oldFiber]形式存储在Map结构中，方便快速查找const newFiber = updateFromMap(existingChildren,returnFiber,newIdx,newChildren[newIdx],lanes,);if (newFiber !== null) {if (shouldTrackSideEffects) {if (newFiber.alternate !== null) {// 如果newFiber是通过复用创建的, 则清理map中对应的老节点existingChildren.delete(newFiber.key === null ? newIdx : newFiber.key);}}lastPlacedIndex = placeChild(newFiber, lastPlacedIndex, newIdx);// 更新resultingFirstChild结果序列if (previousNewFiber === null) {resultingFirstChild = newFiber;} else {previousNewFiber.sibling = newFiber;}previousNewFiber = newFiber;}
}
// 3. 善后工作, 第二次循环完成之后, existingChildren中剩余的fiber节点就是将要被删除的节点, 打上Deletion标记
if (shouldTrackSideEffects) {existingChildren.forEach((child) => deleteChild(returnFiber, child));
}

所以无论是单节点还是多节点、可迭代节点的比较, 最终的目的都是生成下级子节点. 并在reconcileChildren过程中, 给一些有副作用的节点(新增, 删除, 移动位置等)打上副作用标记, 等待 commit 阶段(Renderer)的处理.

时间复杂度

Diff 算法并非 React 独创，React 只是在传统 Diff 算法做了优化，将 diff 算法的时间复杂度一下子从 传统递归O(n^3)降到 两次循环O(n)，其中n是树中元素数量。为了降低算法复杂度，React中对Diff算法做了以下优化：
1、同级对比
只对同级元素进行Diff。如果一个DOM节点在前后两次更新中跨越了层级，那么React不会尝试复用他，即对相同层级的 虚拟DOM 节点进行比较，同一个父节点下的所有子节点。当发现节点已经不存在时，则该节点及其子节点会被完全删除掉，不会用于进一步的比较。这样只需要对树进行一次遍历，便能完成整个 DOM 树的比较。
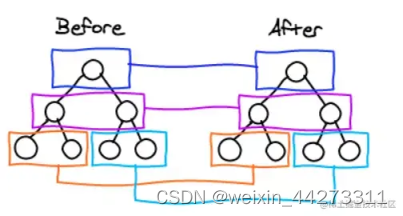
在这里插入图片描述
如果DOM节点前后更新跨越了层级，React则不会复用，直接新建节点并删除原来节点：

在这里插入图片描述
2、类型比较
当比较两个节点时，首先检查它们的类型。如果类型不同，React 会销毁旧节点，并建立新节点。这种类型检查适用于不同的HTML标签或不同的组件类型。

3、Key标识
在处理动态子元素列表时，React 使用 keys 来识别每个元素的唯一性。这有助于确定哪些元素在重新渲染时保持不变，哪些元素需要更改。合理使用 keys 可以极大地提高性能，尤其是在列表和动态内容中。

4、避免不必要的 DOM 操作
通过比较新旧虚拟DOM树，React 可以确定实际需要进行的最小 DOM 更新，从而避免不必要的操作。一个虚拟DOM的Key和Type一样就认为该节点可以复用。

5、批量更新与异步渲染
React 会将多个 setState/useState 调用合并成一个批量更新，以减少渲染次数。React 17 及以后版本中，引入了新的并发模式，允许更灵活的异步渲染。

优化策略

基于React对于传递Diff的优化总结，我们可以通过以下方式来进行优化，简化对比：

  • Keys：在列表中使用唯一的key可以帮助React识别哪些元素改变了，哪些没有。这样React可以只重新渲染那些改变了的元素，而不是整个列表。
  • 组件级别的比较：React在比较组件时，如果组件类型相同，则会比较其props和state；如果组件类型不同，则会销毁旧组件并创建新组件。
  • 避免不必要的重新渲染：使用shouldComponentUpdate、React.memo或PureComponent来避免不必要的渲染。
  • 虚拟DOM树的结构优化：合理的组织组件结构，避免过深的虚拟DOM树，可以减少diff算法需要比较的节点数，从而提高性能。
  • 使用不可变数据：这可以帮助快速比较props和state的变化，因为不可变数据在发生变化时会产生一个新的对象。
  • 懒加载组件：对于大型应用中的一些不常用组件，可以使用懒加载技术，只有当这些组件需要被展示时，才加载它们。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/626034.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Python入门-字面量，函数,类

Python入门-字面量，函数,类

Python 中常用的有6种值&#xff08;数据&#xff09;的类型 (1)字符串需要用英文的双引号包围起来&#xff0c;比如打印"helloworld" &#xff08;2&#xff09;浮点数&#xff0c;整数&#xff0c;字符串等字面量的写法 &#xff08;3&#xff09;字符串定义及打印…
阅读更多...
【极光系列】springboot集成redis

【极光系列】springboot集成redis

【极光系列】springboot集成redis tips&#xff1a;主要用于快速搭建环境以及部署项目入门 gitee地址 直接下载源码可用 https://gitee.com/shawsongyue/aurora.git模块&#xff1a;aurora_rediswindow安装redis安装步骤 1.下载资源包 直接下载解压&#xff1a;https://pa…
阅读更多...
汇编和c++初学，c++字符串加整型，导致的字符串偏移

汇编和c++初学，c++字符串加整型，导致的字符串偏移

从汇编角度分析"helloworld"1 “helloworld”1对应 mov dword ptr [a],1 mov eax,dword ptr [a] add eax,offset string "helloworld" (03CCCBCh)eax地址偏移加了1&#xff0c; lea ecx,[test]最终取的内存偏移地址&#xf…
阅读更多...
【遥感专题系列】影像信息提取之——面向对象的影像分类技术

【遥感专题系列】影像信息提取之——面向对象的影像分类技术

“同物异谱&#xff0c;同谱异物”会对影像分类产生的影响&#xff0c;加上高分辨率影像的光谱信息不是很丰富&#xff0c;还有经常伴有光谱相互影响的现象&#xff0c;这对基于像素的分类方法提出了一种挑战&#xff0c;面向对象的影像分类技术可以一定程度减少上述影响。 本…
阅读更多...
Go-gin-example 第二部分 jwt验证

Go-gin-example 第二部分 jwt验证

文章目录 使用 JWT 进行身份校验jwt知识点补充认识JWTTOKEN是什么jwt的使用场景jwt的组成headerpayloadsignature 下载依赖包编写 jwt 工具包jwt中间件编写如何获取token 编写获取token的Apimodels逻辑编写路由逻辑编写修改路由逻辑 验证token将中间件接入Gin功能验证模块 续接…
阅读更多...
交友脱单盲盒源码，纸条广场，支持单独抽取/连抽/同城

交友脱单盲盒源码，纸条广场，支持单独抽取/连抽/同城

源码介绍 交友脱单盲盒源码&#xff0c;纸条广场&#xff0c;单独抽取/连抽/同城。 盲 盒交友脱单系统源码包含了学校、爱好、城市、地区、星座等 等信息&#xff0c;具有首页轮转广告和页面美化功能。 首页提供了两款 连抽和高质量底部连抽的选项&#xff0c;并且可以在后台…
阅读更多...
如何通过ISPC使用Xe（核显）进行计算

如何通过ISPC使用Xe（核显）进行计算

我一直以为 ISPC 的 Xe 是只包含独立显卡的&#xff0c;比如 A770 这些&#xff0c;没想到看了眼文档是可以使用核显的&#xff0c;但只能在 Linux 和 Windows 上&#xff0c;macOS 不行&#xff0c;就想试试看。 写本文是因为 ISPC 已经出现了三四个版本的大改&#xff0c;但…
阅读更多...
基于SSM的网上挂号系统的设计与实现

基于SSM的网上挂号系统的设计与实现

末尾获取源码 开发语言&#xff1a;Java Java开发工具&#xff1a;JDK1.8 后端框架&#xff1a;SSM 前端&#xff1a;采用JSP技术开发 数据库&#xff1a;MySQL5.7和Navicat管理工具结合 服务器&#xff1a;Tomcat8.5 开发软件&#xff1a;IDEA / Eclipse 是否Maven项目&#x…
阅读更多...
每日一练：LeeCode-102、二又树的层序遍历【二叉树】

每日一练：LeeCode-102、二又树的层序遍历【二叉树】

本文是力扣LeeCode-102、二又树的层序遍历 学习与理解过程&#xff0c;本文仅做学习之用&#xff0c;对本题感兴趣的小伙伴可以出门左拐LeeCode。 给你二叉树的根节点 root &#xff0c;返回其节点值的 层序遍历 。 &#xff08;即逐层地&#xff0c;从左到右访问所有节点&…
阅读更多...
【设计模式-3.3】结构型——享元模式

【设计模式-3.3】结构型——享元模式

说明&#xff1a;说明&#xff1a;本文介绍设计模式中结构型设计模式中的&#xff0c;享元模式&#xff1b; 游戏地图 在一些闯关类的游戏&#xff0c;如超级玛丽、坦克大战里面&#xff0c;游戏的背景每一个关卡都不相同&#xff0c;但仔细观察可以发现&#xff0c;其都是用…
阅读更多...
java基于Spring Boot的灾害应急救援评估调度平台

java基于Spring Boot的灾害应急救援评估调度平台

灾害应急救援平台的目的是让使用者可以更方便的将人、设备和场景更立体的连接在一起。能让用户以更科幻的方式使用产品&#xff0c;体验高科技时代带给人们的方便&#xff0c;同时也能让用户体会到与以往常规产品不同的体验风格。&#xff08;1&#xff09;鉴于该系统是一款面向…
阅读更多...
C++ 设计模式之外观模式

C++ 设计模式之外观模式

【声明】本题目来源于卡码网&#xff08;题目页面 (kamacoder.com)&#xff09; 【提示&#xff1a;如果不想看文字介绍&#xff0c;可以直接跳转到C编码部分】 【简介】什么是外观模式 外观模式Facade Pattern , 也被称为“⻔⾯模式”&#xff0c;是⼀种结构型设计模式&#…
阅读更多...
WordPress如何修改旧文章的发布日期让其变成新文章发布？

WordPress如何修改旧文章的发布日期让其变成新文章发布？

我们个人网站发展一段时间后&#xff0c;可能就不懂得发布什么内容了&#xff0c;这个时候可以考虑翻看以前的旧文章&#xff0c;必要时对其进行适当修改&#xff0c;然后修改它的发布日期变成当前日期重新发布&#xff0c;这样就会变成新文章重新出现在我们首页的文章列表中。…
阅读更多...
基于Pytorch的身份证及其他证件检测矫正模型应用

基于Pytorch的身份证及其他证件检测矫正模型应用

前言 在做身份证和其他证件识别的时候&#xff0c;图片基本都不是摆正的状态&#xff0c;此时在进行OCR文字识别的提取文字信息的时候会出现很多误差&#xff0c;如何将证件摆正&#xff0c;再进行OCR文字识别就可以大大提高准确率。 准备工作 1、Python环境&#xff0c;在P…
阅读更多...
tda7294功放电路图大全

tda7294功放电路图大全

简易电子管功放电路图&#xff08;一&#xff09; 6P3P单端A类电子管功放电路图 如图为6P3P单端A类电子管功放电路图。VT1、VT2直流通路串联。VT1构成普通的三极管共阴放大器&#xff0c;VTr2构成阴极输出器&#xff0c;对VT1而言VT2是一个带电流负反馈的高阻负载。音频信号由…
阅读更多...
Leetcode2696. 删除子串后的字符串最小长度

Leetcode2696. 删除子串后的字符串最小长度

Every day a Leetcode 题目来源&#xff1a;2696. 删除子串后的字符串最小长度 解法1&#xff1a;暴力 暴力做法是不断把 AB 和 CD 去掉&#xff0c;直到 s 中没有 AB 和 CD 为止。 代码&#xff1a; /** lc appleetcode.cn id2696 langcpp** [2696] 删除子串后的字符串最…
阅读更多...
漏洞复现-金和OA jc6/servlet/Upload接口任意文件上传漏洞（附漏洞检测脚本）

漏洞复现-金和OA jc6/servlet/Upload接口任意文件上传漏洞（附漏洞检测脚本）

免责声明 文章中涉及的漏洞均已修复&#xff0c;敏感信息均已做打码处理&#xff0c;文章仅做经验分享用途&#xff0c;切勿当真&#xff0c;未授权的攻击属于非法行为&#xff01;文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直接或者间接的…
阅读更多...
关于浮点数的四舍五入问题

关于浮点数的四舍五入问题

最近有关注到&#xff0c;在C/C中&#xff0c;对于浮点数的四舍五入&#xff0c;与实际的有一些出入&#xff0c;我打算今天总结一下&#xff0c;并解释一下这是为啥&#xff0c; 好了&#xff0c;下面进入正题&#xff0c;都是干货哦&#xff0c;认真看完&#xff0c;留下你的…
阅读更多...
西米支付：到底什么是NFT（数字藏品支付通道）（NFT支付通道）

西米支付：到底什么是NFT（数字藏品支付通道）（NFT支付通道）

NFT到底指的是什么呢&#xff1f; 数字藏品的实际意义在于它们打破了传统艺术品的物质形态束缚。数字藏品可以通过虚拟现实和区块链技术进行创作、展示和交易。它们不仅可以满足人们对艺术品的审美需求&#xff0c;还可以成为一种投资和资产保值增值的方式。数字藏品的实际意义…
阅读更多...
排序——归并排序

排序——归并排序

文章目录 基本思想递归版本思路代码实现 非递归版思路代码实现 特性结果演示 基本思想 归并排序&#xff08;MERGE-SORT&#xff09;是建立在归并操作上的一种有效的排序算法,该算法是采用分治法&#xff08;Divide andConquer&#xff09;的一个非常典型的应用。将已有序的子…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023