题目

下载附件后，我们看到的是这样一个界面，这里需要理解RSA的构造

RSA原理理解

RSA加密算法是一种非对称加密算法，在公开密钥加密和电子商业中被广泛使用。对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。假如有人找到了一种快速因数分解的算法，那么用RSA加密的信息的可靠性就会极度下降。但找到这样算法的可能性是非常小的。今天只有短的RSA钥匙才可能被暴力方式破解。到目前为止（2021年），世界上还没有任何可靠的攻击RSA算法的方式。只要其密钥的长度足够长，用RSA加密的信息实际上是不可能被破解的。

加密由公钥，私钥，明文，密文，四部分组成。

前提：公钥（7，33）和私钥（3，33）中的，7，33（这两个33是同一个数字）只有私钥中的3是不公开的。

过程1：现在假设我们用这个公私钥对去发送消息C A O，假如字符转换为的十进制数字的规则就是序号顺序，那么C A O 对应的就是3 1 15

过程2：这时候就用到了公钥中的第一个数字7，也就是对3进行7次方，1进行7次方，15进行7次方，结果分别是2187 1 170859375

过程3：使用公钥的第二个数字33，对上面数字进行求余。2187%33=9 1%33=1 170859375%33=27 最后得到的9 1 27就是密文

将得到的密文发送给接收方，接收方再进行解密

解密过程：

1.由发送方可以得到9 1 27，依次对其进行3次方，这里的3次方的3就是私钥中的3.分别得到 729 1 19683

2.再对上面求得数字进行求余 729%33=3 1%33=1 19683%33=15 这里的33就是公钥和私钥公开的数字

3.上一步求解得到的3 1 15是不是很眼熟，没错就是要发送的信息，也就是明文

那么可以用公钥加密，私钥解密，同时，也就是可以用私钥解密，公钥加密

总结：如果用E代表7 ，N代表33 D代表3，那么公钥可以写成（E,N）私钥可以写成（D,N),那么得到密文（也就是加密）的公式就是

密文=明文的E次方%N 明文=密文的D次方%N

那么公钥和私钥该如何确定？

五个步骤：

1.任意选择两个质数

2.两个质数相乘

3.计算欧拉函数

4.选公钥

5.计算私钥

具体如图。

题目应用解题

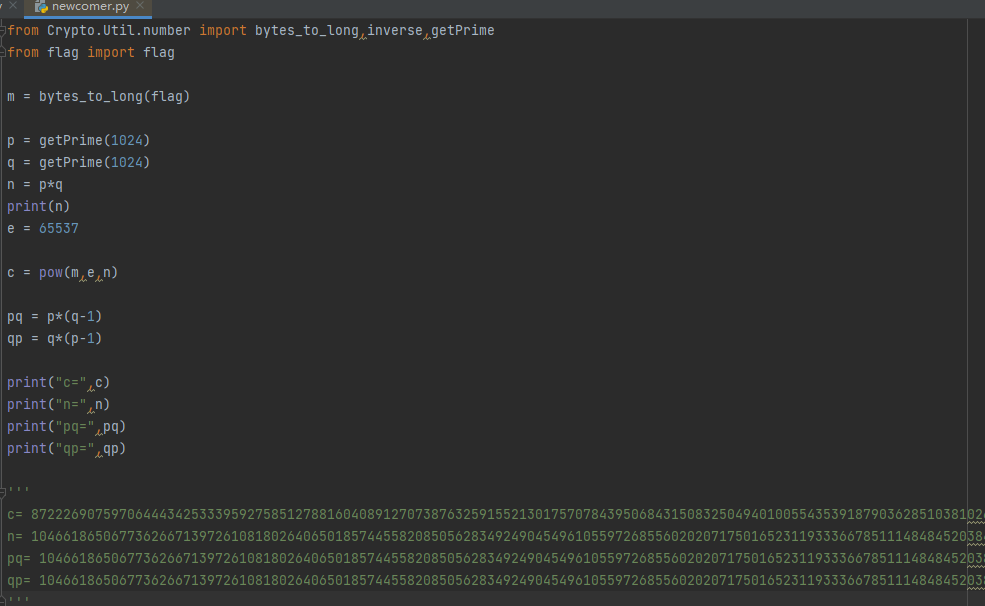
我们再来分析代码：每一段代码的意思都有解释

from Crypto.Util.number import bytes_to_long,inverse,getPrime
from flag import flag
​
​
#这里是将明文m转换为字符串flag
m = bytes_to_long(flag)
​
#生成两个1024的质数 p q
p = getPrime(1024)
q = getPrime(1024)
#两个质数相乘也就是N,这里用n表示而已
n = p*q
print(n)
​
#给出指数E,也就是公钥中的E
e = 65537
​
#计算密文c =m的e次方%n
c = pow(m,e,n)
​
​
#给出了pq qp的关系
pq = p*(q-1)
qp = q*(p-1)
​
#给出相关参数
print("c=",c)
print("n=",n)
print("pq=",pq)
print("qp=",qp)
​
'''
c= 8722269075970644434253339592758512788160408912707387632591552130175707843950684315083250494010055435391879036285103810263591951437829414438640307561645721347859659807138051841516634704123100270651976676182059252251162982609391666023674158274992400910869692389001622774140191223807887675081808561012755545464977015973615407965906513878979919700065923364884766974187303774330319143647840846354404070430118235352622445115153298578370521811697710289716188726587743282814946239856766713516166990341116198180068191759095913957606379780234116317390622824096667107736103270907349927467971817639795094030622157581511033950777
n= 10466186506773626671397261081802640650185744558208505628349249045496105597268556020207175016523119333667851114848452038431498926527983706092607207796937431312520131882751891731564121558651246025754915145600686076505962750195353958781726515647847167067621799990588328894365930423844435964506372428647802381074584935050067254029262890188260006596141011807724688556673520261743199388391094490191001701011230322653422314758778116196105077883955436582364267530633358016652912054880813710531145973799193443828969535902856467548523653920307742364119002349899553478815101092655897400295925170383678499125295006364960124859003
pq= 10466186506773626671397261081802640650185744558208505628349249045496105597268556020207175016523119333667851114848452038431498926527983706092607207796937431312520131882751891731564121558651246025754915145600686076505962750195353958781726515647847167067621799990588328894365930423844435964506372428647802381074488896197029704465200125337817646702009123916866455067019234171839614862660036737875747177391796376553159880972782837853473250804807544086701088829096838316550146794766718580877976153967582795248676367265069623900208276878140709691073369415161936376086988069213820933152601453587292943483693378833664901178324
qp= 10466186506773626671397261081802640650185744558208505628349249045496105597268556020207175016523119333667851114848452038431498926527983706092607207796937431312520131882751891731564121558651246025754915145600686076505962750195353958781726515647847167067621799990588328894365930423844435964506372428647802381074475956379708898904933143429835002718457573266164923043251954374464149976302585916538814746811455883837138715445492053610047383292461097590195481556557381952895539341802954749542143253491617052100969586396996063822508764438280468492894012685918249843558593322831683872737943676955669923498182824352081785243246
'''

再来看解密的代码

from Crypto.Util.number import bytes_to_long, long_to_bytes, inverse, getPrime
​
c = 8722269075970644434253339592758512788160408912707387632591552130175707843950684315083250494010055435391879036285103810263591951437829414438640307561645721347859659807138051841516634704123100270651976676182059252251162982609391666023674158274992400910869692389001622774140191223807887675081808561012755545464977015973615407965906513878979919700065923364884766974187303774330319143647840846354404070430118235352622445115153298578370521811697710289716188726587743282814946239856766713516166990341116198180068191759095913957606379780234116317390622824096667107736103270907349927467971817639795094030622157581511033950777
n = 10466186506773626671397261081802640650185744558208505628349249045496105597268556020207175016523119333667851114848452038431498926527983706092607207796937431312520131882751891731564121558651246025754915145600686076505962750195353958781726515647847167067621799990588328894365930423844435964506372428647802381074584935050067254029262890188260006596141011807724688556673520261743199388391094490191001701011230322653422314758778116196105077883955436582364267530633358016652912054880813710531145973799193443828969535902856467548523653920307742364119002349899553478815101092655897400295925170383678499125295006364960124859003
pq = 10466186506773626671397261081802640650185744558208505628349249045496105597268556020207175016523119333667851114848452038431498926527983706092607207796937431312520131882751891731564121558651246025754915145600686076505962750195353958781726515647847167067621799990588328894365930423844435964506372428647802381074488896197029704465200125337817646702009123916866455067019234171839614862660036737875747177391796376553159880972782837853473250804807544086701088829096838316550146794766718580877976153967582795248676367265069623900208276878140709691073369415161936376086988069213820933152601453587292943483693378833664901178324
qp = 10466186506773626671397261081802640650185744558208505628349249045496105597268556020207175016523119333667851114848452038431498926527983706092607207796937431312520131882751891731564121558651246025754915145600686076505962750195353958781726515647847167067621799990588328894365930423844435964506372428647802381074475956379708898904933143429835002718457573266164923043251954374464149976302585916538814746811455883837138715445492053610047383292461097590195481556557381952895539341802954749542143253491617052100969586396996063822508764438280468492894012685918249843558593322831683872737943676955669923498182824352081785243246
#由n=pq pq=p*(q-1)= 则p=n-pq=pq-p*(q-1)=pq-pq+p,q同理
p = n - pq
q = n - qp
​
#这里的phi可以理解为上图中的T,也就是欧拉函数
phi = (p - 1) * (q - 1)
​
e = 65537
#inverse函数可以求出私钥中的D，通过求逆的方式的出私钥D
d=inverse(e,phi)
# 看了WriteUp才知道原来有专门的求逆的函数，我还瞎折腾这么久T_T
#有了私钥D，就可以得出明文 m=密文（m)的d(私钥中的第一个数字)次方对n（两个质数的结果，也就是公私钥中的N)
m=pow(c,d,n)
#再将数字m转换为字符串就可以得到flag
flag=long_to_bytes(m)
print(flag)

b'flag{719014b3-c4e1-4f81-a7be-b4f0d65c9e10}'