动态规划
动态规划相信大家都知道，动态规划算法也是新手在刚接触算法设计时很苦恼的问题，有时候觉得难以理解，但是真正理解之后，就会觉得动态规划其实并没有想象中那么难。网上也有很多关于讲解动态规划的文章，大多都是叙述概念，讲解原理，让人觉得晦涩难懂，即使一时间看懂了，发现当自己做题的时候又会觉得无所适从。我觉得，理解算法最重要的还是在于练习，只有通过自己练习，才可以更快地提升。话不多说，接下来，下面我就通过一个例子来一步一步讲解动态规划是怎样使用的，只有知道怎样使用，才能更好地理解，而不是一味地对概念和原理进行反复琢磨。
本题很明显
- 状态表示dp【i】为第n个泰波那契数，
- 编辑本题是第一种情况，后面的题目我们会不断遇到1，2，3的情况，我们后面再细讲
- 而状态转移方程为题目也直接给了出来， Tn+3 = Tn + Tn+1 + Tn+2，状态转移方程： Tn = Tn -1+ Tn-2 + Tn-3
- 初始化（防止越界的情况）：本题很明显Tn-3的时候当，n小于3的时候会出现越界的情况，因此我们要提前初始化好dp【0】 ，dp【1】，dp【2】
- 填表顺序： 左到右
编辑 - 返回值；dp【n】
细节问题：
- 当n<3的时候，就不需要进行Tn = Tn -1+ Tn-2 + Tn-3计算因此就可以直接返回
空间优化问题：
本题如果我们按照上面的写法的话，就需要开辟一个n+1大小的vector数组dp，当我们在计算第n个位置的时候，我们只需要n-1，n-2，n-3的位置，如果前面还有n-4和n-5都不需要的
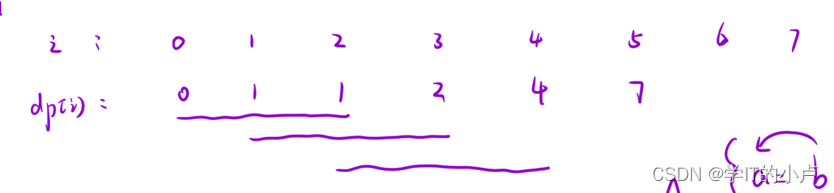
因此我们就可以直接用三个变量a，b，c来优化，使得空间复杂度为o(1)
面试题 08.01. 三步问题
分析一下题目的意思：
当从0号台阶到1号台阶，只有1种方法；
当从0号台阶到2号台阶，我们可以直接从0号台阶蹦到2号台阶，也可以从0-1-2，总共两种解法
当从0号台阶到3号台阶，我们可以从0号直接蹦到3号台阶，也可以0-1-2-3和0-2-3和0-1-3，总共4种解法
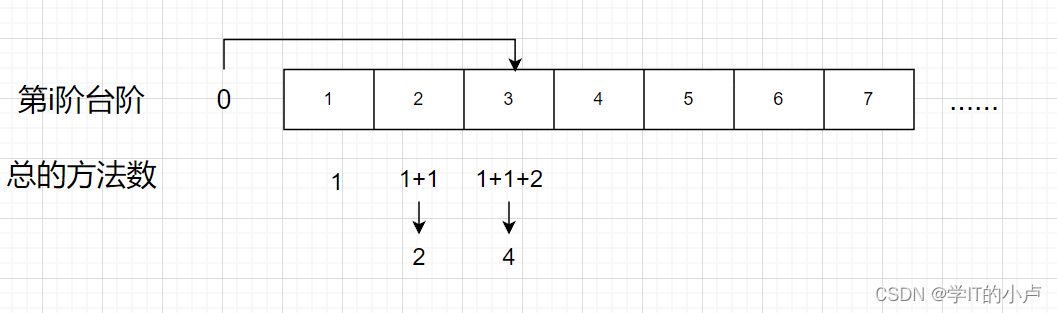编辑 眼尖的同学这个时候以及发现了状态转移方程了，我们注意一下（以到4号台阶为例)：我们可以看成从1号到4的方法数+2号到4号的方法数+3号到4号的方法数
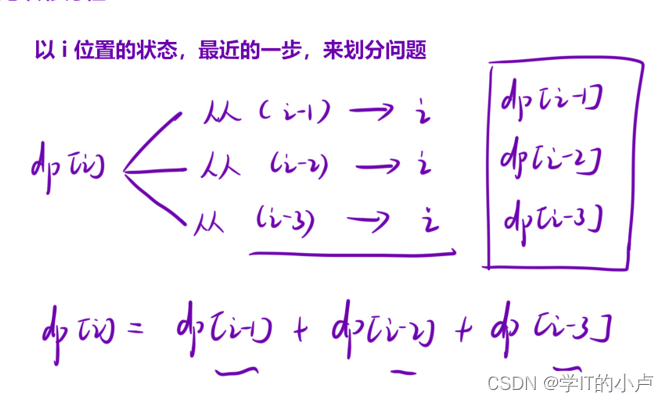
- 因此我们的状态表示dp【i】就表示到达第i号台阶的方法数
- 状态转移方程：
编辑
此时有的同学会有一个疑问：就是我从i-2号台阶到i号台阶的时候不是有两种情况：
- i-2到i
- i-2先到i-1再到i号台阶
其实不然：i-2先到i-1的这种情况以及是包含在i-1到i的方法数中
- 初始化（防止越界的情况）：本题很明显Tn-3的时候当，n小于3的时候会出现越界的情况，因此我们要提前初始化好dp【0】 ，dp【1】，dp【2】
- 填表顺序： 左到右
- 返回值；dp【n】
解题思路：
本题的状态表示是通过经验+题目要求得出的
状态表示：dp[i]代表以i位置结尾的所有解码方法总和
状态转移方程：
编辑
我们就观察以i位置结尾的数字串，此时有两种情况：
- s[i]单独解码
- s[i]和s[i-1]一起解码
先说s【i】单独解码的情况，当解码成功时，也就是s【i】代表的数字属于【1，9】，则dp【i】+=dp【i-1】，失败的话就是0了
再来就是 s[i]和s[i-1]一起解码 的情况：当解码成功也就是这两个数字属于【10,26】,则dp【i】+=dp【i-2】，失败也是0
初始化：dp【0】当s【0】属于1-9，dp【0】=1，s【0】=0的话dp【0】=0
dp【1】的话，此时就有两个数字，就分为两种情况，两个数字分开单独解码和两个数字一起解码，单独解码的话s【1】代表的数字属于【1，9】，dp【1】++，两个数字一起解码的话，当解码成功也就是这两个数字属于【10,26】,则dp【1】++
填表顺序：从左导游
返回值;dp[n-1]
解题代码：
class Solution {
public:int numDecodings(string s) {int n = s.size();vector<int>dp(n + 1, 0);//初始化if (s[0] >= '1' && s[0] <= '9')dp[0] = 1;else dp[0] = 0;if (n == 1)return dp[0];if (dp[0] && s[1] - '0')dp[1]++;int num = (s[0] - '0') * 10 + (s[1] - '0');if (num >= 10 && num <= 26)dp[1]++;for (int i = 2; i < n; i++){if (s[i] >= '1' && s[i] <= '9')dp[i] += dp[i - 1];num = (s[i - 1] - '0') * 10 + (s[i] - '0');if (num >= 10 && num <= 26)dp[i] += dp[i - 2];}return dp[n - 1];}
};
91. 解码方法
处理边界问题及初始化问题的的技巧：
我们可以给dp数组多开一个位置，也就是开n+1个空间，使整个数组向右移动一位
这样我们原本的dp【1】也可以移到循环中进行计算了！！！
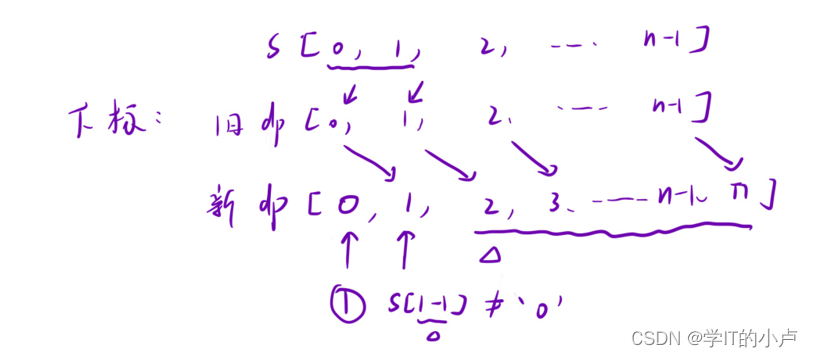编辑
这里的0,1,2等都是下标
因此我们多出来一个位置0号下标的值是多少呢？
因为我们后面要计算dp【2】也就是原本的dp【1】的时候会运用到dp【i-2】和dp【i-1】
因为dp【i-1】不会出错，所以我们只需要注意dp【i-2】的正确性
当dp【2】时，也就是两位数字的解码方案数，当我们运用到dp【i-2】的时候，这个是两位数字一起解码，因此dp【i】+=dp【i-2】如果dp【0】为0，即使解码成功也等于没有解码成功，因此这里dp【0】要为1
优化后的代码：
class Solution {
public:int numDecodings(string s) {int n=s.size();vector<int>dp(n+1);dp[0]=1;//初始化if(s[0]>='1'&&s[0]<='9')dp[1]=1;else dp[1]=0;if(n==1)return dp[1];/*if(dp[0]&&s[1]-'0')dp[1]++;int num=(s[0]-'0')*10+(s[1]-'0');if(num>=10&&num<=26)dp[1]++;*/for(int i=2;i<=n;i++){if(s[i-1]>='1'&&s[i-1]<='9')dp[i]+=dp[i-1];int num=(s[i-2]-'0')*10+(s[i-1]-'0');if(num>=10&&num<=26)dp[i]+=dp[i-2];}return dp[n];}
};
