一. 介绍
在点对点的通信中,信源编码定理(source coding theorem)满足可达性和可逆性。当信道是无噪声时,那么Y=X,这时就不需要信道编码。但是,信源编码依旧是有效的,可以提高数据传输效率,信源编码的单位通常是bits/source symbol。
信源编码其实跟我们通常所说的数据压缩(data compression)很类似。信源整个可能序列记为,根据典型集理论,只有部分序列是有效的。讲这些有效的序列编号从1~|A|,由此可得:
信源编码端:
当从有效序列中抽取信源符号时,信源编码则输出对应的下标。
否则,输出一个固定的常数。
译码端:
当收到一个下标i时,则输出集合A中对应的序列。
二. 信源编码定理
信息论比较关注可靠传输的界限,接下来我们将从理论上证明存在对应的信源编码方案。
2.1 统计堆理论
信源编码会用到一个有意思的理论,叫做统计堆理论(binning)。输入一个序列,我们将其随机放到一个搁架里面,在同一个搁架里面的物体下标均一致。如果以上过程是按照均匀且随机的形式进行分配的,那么该过程称之为random binning。
借助选择引理(selection lemma),当以上分配过程的平均错误率接近于0时,也就可以说明信源编码的错误率趋近于0.
2.2 信源编码与压缩率
将一个离散无记忆的信源记作:
其中P代表概率分布。信息与通信理论告诉我们压缩后的长度不能太短,其界限跟U的香农熵是一样的,也就是可达的压缩率为:
![]()
换句话说可达的压缩率需要满足:
解释:
根据随机统计堆理论(random binning),当把信源序列随机映射到有限数量的搁架里面时,只要搁架的数量大于:
则可以保证每个搁架里面只会存在一个序列,不会有重复的情况出现,也就是发生这种情况的概率很小,则可以保证译码不会出错。
三. 信源编码方案设计
令且是一个很小的数,
是一个正整数,
为压缩率。将信源编码方案
记作:
2.1 统计堆
从信源中选取典型集:
我们将典型集中的一个序列随机放入一个搁架中,搁架的编号(index)为:
此过程可以看成如下函数:
此映射规则全局公开。
2.2 编码过程
给定一个序列时,当序列属于典型集,也就是:
则利用映射函数生成m,如下:
如果非典型集序列,则可以直接输出m=1
2.3 译码过程
给定一个消息m,译码为,其满足两个条件:
第一个条件要求属于典型集。第二个条件要求编码和译码结果一致且唯一。
如果不满足任何一个条件,则输出错误“?”。
四. 理论分析
以上解释的信源编码方案的平均错误概率记为:
将发生译码错误的事件分成两种情况可得:

第一个事件代表编码前的序列不属于典型集。
第二个事件代表译码后的序列不在有效的集合中。
由此平均错误概率可以表示为:
根据并集定理(union bound)可得:
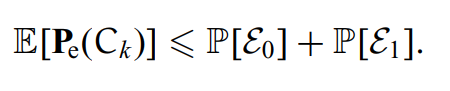
先来分析下第一个事件。
根据信息论中的渐近等分性(AEP),第一个非典型集的概率很小,如下:
![]()
接着分析下第二个事件。
我们主要考虑错误概率的上界,如下:

第一个等号:将该事件表示为求和
第一个不等号:关注两个不同的序列编码后是相同的值概率,也就是位于同一个搁架里面
第二个等号:每个架子的概率
第二个不等号:求和的情况与典型集的大小一样
第三个不等号:典型集的定义
最后一个不等号:P总概率求和为1
根据以上讨论,我们需要让压缩率满足:
这样就可以保证:
![]()
最后可得统计堆理论的平均错误概率满足:
根据选择引理,理论上一定可以找到一种编码方案,使其满足:
其中是一个很小的数,也就是压缩率需要满足:
反过来可逆性也是一样的。推导如下:
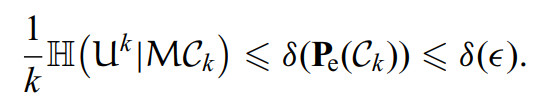
对熵进行讨论:
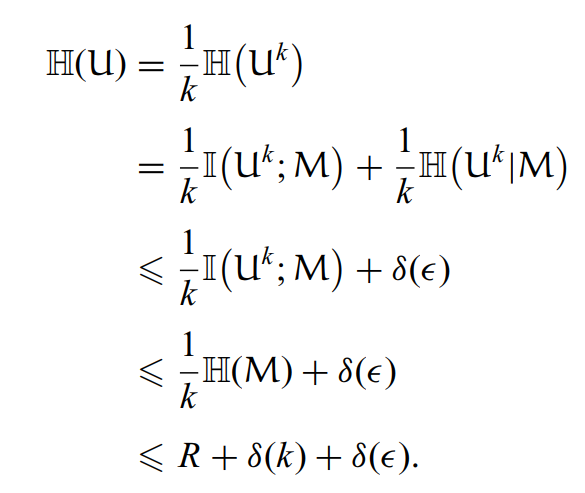
五. 小结
(1)子带编码
将连续信源产生的输出用多个带通滤波器进行滤波,只要这些滤波器是按照镜像滤波器成对设计的,这些滤波器的输出相加就可以无失真恢复原信号。信号进入带通滤波后再分别进行编码,各个子带的频谱特性相对平坦一些,样点之间的相关性减小,加之不同子带在进行编码时可以根据它的重要性分配不同的比特数,因此可以压缩编码数据。
(2)基于信源模型假定的编码方法
如果信源特性可以采用某种数学模型描述,那么基于这个模型进行压缩编码,可以获得更高的编码效率。
例如:语音信号可以用语音产生的声道模型进行描述,因而只要对估计出的声道模型参数和激励信号进行编码,接收端就可以重新合成出与原信号感觉上相类似的信号,这就是声码器技术。由于全极点声道模型抓住了语音信号共振峰特性的本质,计算上十分简捷,因此以线性预测为中心的一大类声码器在语音信号压缩编码方面取得了很大成功。包括:LPC 声码器、CELP 声码器、多带激励(MBE)声码器等。
基于声码器技术,压缩语音编码数据率的效率是非常高的,例如将 64Kbps 的 PCM 语音信号压缩到 8Kbps左右时,恢复语音的音质还可以是透明的;压缩到600bps时,恢复语音的可懂度还能接近100%。
(3)变换域编码
将连续信源产生的输出采用某种正交变换进行变换,变换域中各个信号分量的相关性大大减小,于是可以根据各个分量的重要性进行量化编码,可以大幅度减小比特率。常用的正交变换有离散傅立业变换、离散余弦变换、小波变换等。这些变换都是可逆的,接收端采用逆变换对于在变换域量化编码的结果进行逆变换,就可近似恢复原信号。这些编码算法在图像压缩编码,网络安全设计等方面取得了很大的成功。




![[数据结构与算法]数据结构基础、排序算法详解、算法思想详解、领域算法详解------](http://pic.xiahunao.cn/[数据结构与算法]数据结构基础、排序算法详解、算法思想详解、领域算法详解------)















