人工智能 （AI） 也加入了这一行列，从物理学中汲取灵感，开发最先进的模型，并告知它们在基础层面上是如何工作的。虽然物理学的思想以前已经被整合到人工智能中，但直到最近，这些模型才以如此不屈不挠的方式超越了其他方法，如DALL-E 2和Stable Diffusion等模型。

        在本文中，我们将从高层次上了解这些最新进展，并展示来自物理学两个不同子领域（静电学和热力学）的概念如何将生成式 AI 模型的性能提升到一个新的梯队。

使用静电原理生成人脸图像的生成式 AI 模型（由 PFGM 作者提供）

        本文面向任何对这些强大模型如何工作的高级概念感兴趣的人。我们不会涉及特定的数学细节，因此解释应该对人工智能所有经验水平的读者都有帮助。

二、静电学和热力学的教训

        我们将要研究的这两种情况最常应用于图像的生成式 AI。对于静电学，将概率密度处理为电荷密度是该方法的核心，其中可以利用根据物理定律的电子运动来生成新颖的图像。

        在热力学的第二种情况下，将图像中的像素视为原子是该方法的核心，其中这些原子在时间上向前和向后的自然运动同样可以被利用来生成图像。

现在让我们来看看第一个案例。

三、具有静电的生成式 AI

        静电学可以看作是对电荷的研究。电荷密度是连续物体，在不同区域具有不同的电荷量。与电荷密度低的区域相比，高电荷密度的地方会以更大的力排斥（或吸引）电子。

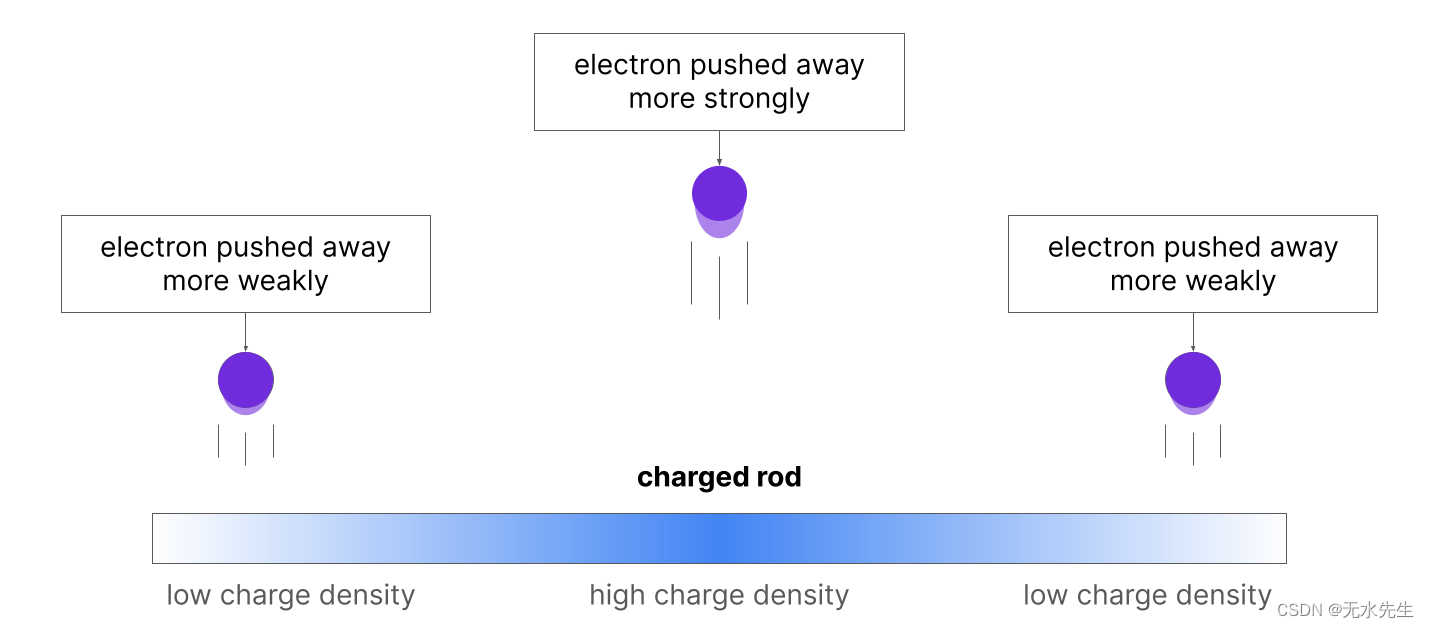
这种带电的棒在棒上的不同点具有不同的电荷量（电子数）

        我们可以绘制出该杆的电荷密度 - 对于杆上的每个点，我们绘制出该点的“多少”电荷。正如我们所看到的，中间有很多电荷，在杆的两端逐渐减少到较低的电荷。

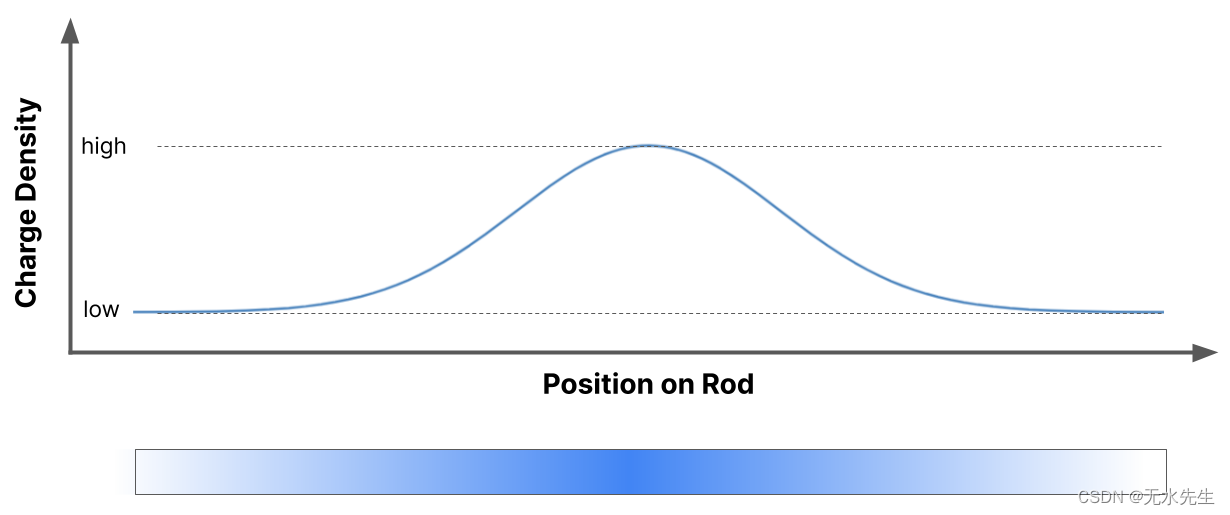
在杆上的每个点上，曲线的高度指定了电荷密度

        另一方面，也有概率密度。这些曲线显示了某物每个值的可能性。下面，我们显示了人类男性身高的概率密度曲线。正如我们所看到的，身高为 5 英尺 11 英寸（71 英寸，180 厘米）的男性是相当可能的，而比这更高或更矮的身高不太可能。

人类男性的身高分布可以用类似的方式绘制

        您可能已经注意到，这些曲线看起来非常相似。一类特定的生成式 AI 模型 - 泊松流生成模型 （PFGM） - 也观察到了这一点。PFGM 的工作原理是将概率密度视为电荷密度。

        具体来说，为了生成数据，我们需要从该类型数据的概率分布中抽样。如果我们想生成一个逼真的人类样本（只考虑身高和体重），他们不太可能看起来像这样：

        这种不太可能的身高和体重形成更不可能的组合，并且更不可能一起作为三元组样本

        特别是，不太可能出现那么高那么瘦，或者那么矮那么宽的人，更不用说同时拥有 3 个这样的极端的样本了。我们需要能够根据身高和体重组合的可能性从分布中进行采样，以便生成更真实的新颖数据，如下所示：

仅考虑身高和体重，这个男性样本比上述样本要现实得多

        通过生成式 AI，我们尝试使用一组示例数据点来了解可能有哪些组合来生成真实的数据。这组示例数据点称为训练数据，它决定了我们将生成哪种类型的数据。例如，如果我们的训练数据是人脸图像，那么我们将训练模型以生成人脸图像。

这与静电有什么关系？

3.1 作为电荷分布的数据分布

通常，学习生成类似于训练数据的样本可能很困难。PFGM 没有尝试直接做到这一点，而是利用静电的巧妙技巧来规避这个问题。

PFGM 不再将数据视为概率分布，而是改变视角并将此分布视为电荷分布。更有可能的数据点（更高的概率密度）被认为具有更多的电荷（更高的电荷密度）。

就其本身而言，这并没有多大帮助 - 但PFGM利用了一个关键事实：当被视为电荷分布时，该分布将自我排斥。随着时间的流逝，这种排斥力会“膨胀”，并逐渐将分布转变为一个大的均匀半球。我们可以在下面看到这个过程的视频：

当被视为电子时，训练数据会随着时间的推移自行排斥形成一个均匀的半球（由 PFGM 作者提供）

我们看到，示例心形分布通过在每个点上遵循轨迹（如下面的黑色曲线所示）而演变为半球分布。

对于数据中随机选择的几个点（心形），我们看到将它们映射到半球的轨迹（黑色曲线）（来源)

        这个过程对我们有什么帮助？我们之前说过，很难从数据分布中抽样，这是我们的最终目标。从这个均匀的半球取样并不困难。由于它是如此均匀和规则，我们只需随机选择其上的任何点即可从半球采样。

        让我们利用这个事实：我们不是尝试直接对数据分布进行建模并直接从中采样，而是在均匀半球上对一个点进行采样，然后使用物理场将其映射回数据分布。泊松流生成模型的目标是学习轨迹曲线，如上图所示。这些曲线由物理定律产生，提供了两个分布之间的映射。

        由于正常的正向时间物理学将数据沿轨迹映射到半球，因此我们使用 PFGM 在时间上向后映射到另一个方向。我们没有尝试直接对数据的概率分布进行建模，而是对复杂概率分布和简单半球分布之间的转换进行建模，我们可以轻松地从中选择点。

我们了解物理定律如何在数据分布之间映射，以便从易于采样的数据中生成新颖的图像

        整个过程如上图所示。总结一下：

1. 我们的最终目标是新数据。我们无法通过直接从数据分布中采样来达到目的，因为直接采样太复杂了。
2. 物理定律将这种复杂的数据分布转化为简单的半球分布
3. 我们的 PFGM 为我们特定的训练数据集学习这种转换（即轨迹）。
4. 然后我们从半球取样，这很容易做到
5. 一旦我们有了这个样本，我们就会反向运行物理，沿着我们刚刚学到的这些轨迹向后移动，得出数据分布，从而生成新的数据。

        如果这令人困惑，请不要担心 - 这是一个难以理解的概念。重要的部分是，物理学在我们想要的（新数据）和我们可以轻松获得的（半球数据）之间架起了一座桥梁。

我们也可以在其他领域利用这种方法——现在让我们来看看我们如何利用热力学来做到这一点。

3.2 具有热力学的生成式 AI

        热力学可以看作是对随机性的研究。例如，如果我们随机地将一堆硬币扔在地上，我们可以问其中 50% 的单挑着地的概率与 100% 的单挑着地的概率相比如何。

        让我们看一下四枚硬币的情况。其中 100%（四个）单挑着陆的概率小于其中只有 50%（两个）单挑着陆的概率。这是因为只有两枚硬币有六种方式可以正面朝上，而所有四种硬币只有一种方式可以正面朝上。

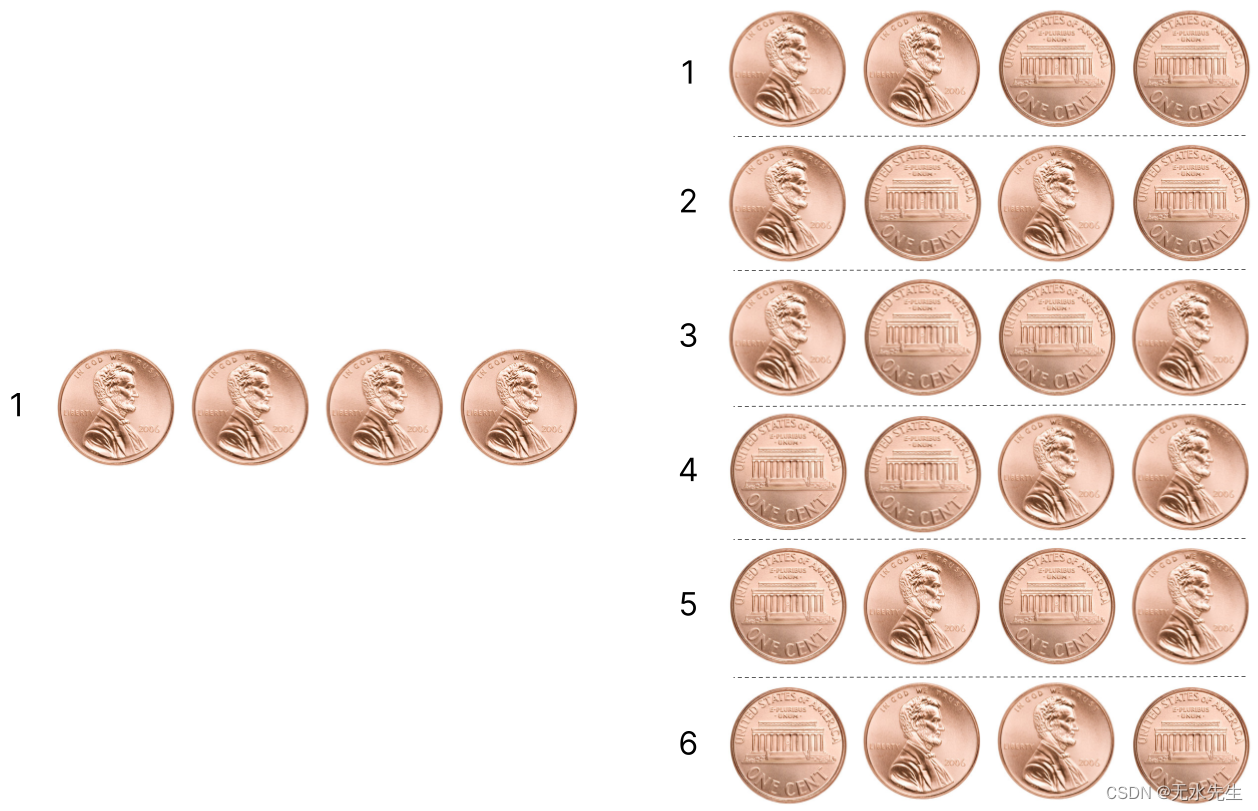
        只有两枚硬币正面朝上有更多方法，因为在两枚硬币正面朝上方面有灵活性，而在四枚硬币的情况下没有这种灵活性——所有硬币都必须正面朝上

        在这种情况下，我们看到 50% 的硬币被单挑的可能性是 100% 的 6 倍。如果我们将同样的思想实验扩展到十个硬币，那么 50%（五个）硬币单挑落地的可能性是 100%（十个）硬币单挑落地的可能性的 252 倍。如果我们将其扩展到仅 50 个硬币，那么这个因素的可能性就会增加 126 万亿倍。如果我们将这个概念扩展到数十亿个硬币呢？

3.3 从硬币到原子：扩散

        热力学将原子铸造为“硬币”，并研究上述现象在物理系统中的后果。例如，如果将一滴食用色素放入一杯水中，食用色素会扩散开来，最终在玻璃杯中形成均匀的颜色。为什么会这样？

随着时间的流逝，食用色素会自然扩散，从而在玻璃杯中形成均匀的颜色（来源)

        均匀的颜色是食用色素原子随时间扩散的结果。数十亿个原子在不同的地方比所有原子在同一个地方的方式要多得多，就像50%的硬币比100%的硬币有更多的方式。当所有原子都集中在一滴中时，它们可以被认为是“100%单挑”;当原子均匀分布时，它们可以被认为是“50%的单挑”。

        请记住，“50%的单挑”状态更有可能发生，并且只会随着硬币数量的增加而变得更有可能 - 只有50个硬币的可能性要高出126万亿倍。当我们将原子视为硬币时，我们必须记住，仅一滴食用色素中就有数万亿个原子。有了这么多的原子，它们最终扩散的可能性就变得比集中的液滴要大得多。因此，只需通过随机运动，当液滴接近这种 50% 的均匀颜色状态时，液滴就会随着时间的推移而扩散开来。

        这个过程被称为扩散，它启发了 DALL-E 2 和 Stable Diffusion 等模型。

3.4 从原子到像素：生成式人工智能中的扩散

        正如热力学将原子视为硬币一样，扩散模型将图像的像素视为原子。与食用色素的随机运动总会导致颜色均匀类似，像素的“随机运动”总会导致“电视静态”，即均匀食用色素的图像等价物。

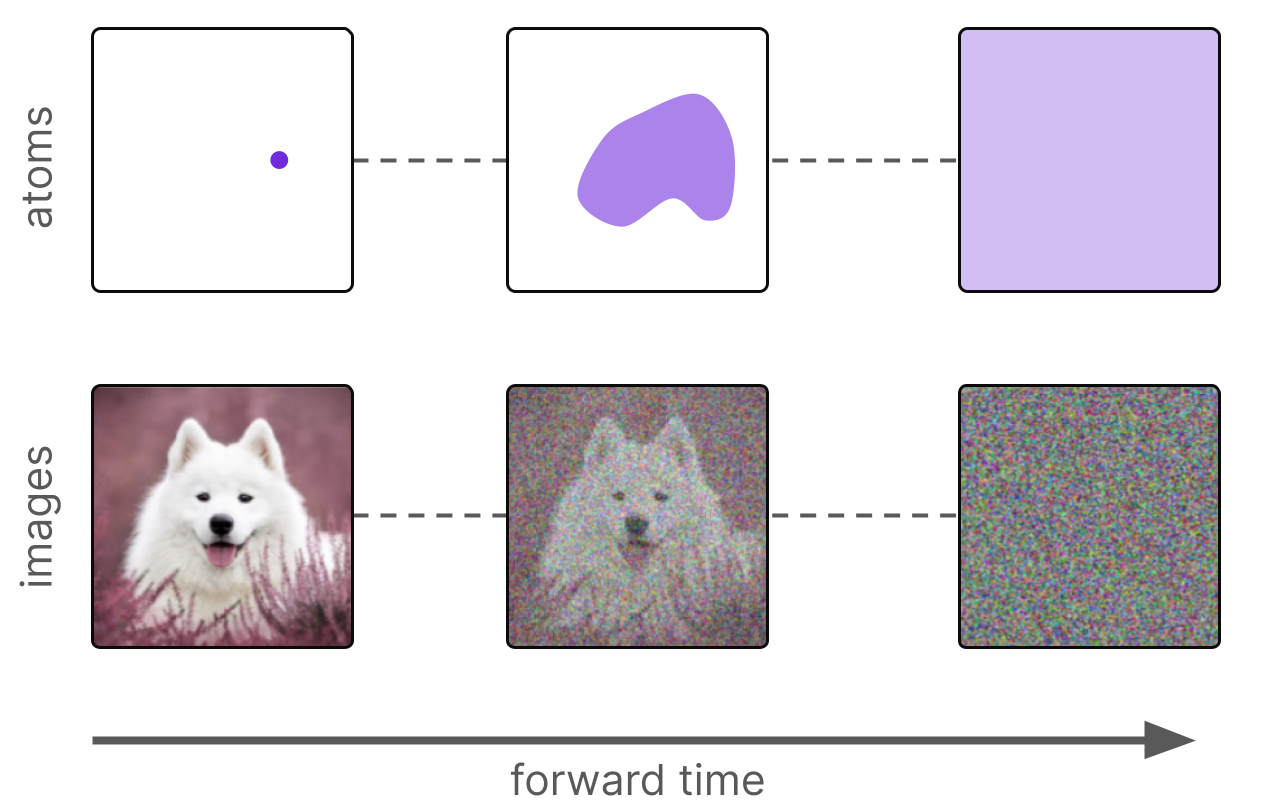
        原子的随机运动总是会导致均匀的颜色，而像素的随机运动（即稍微改变它们的值）总是会导致电视静止

        重要的是，无论我们在哪里放置最初的食用色素滴，随着时间的推移，所有可能的起始位置都会产生相同的均匀颜色的最终状态。

随着时间的流逝，所有起始掉落都接近相同的最终状态

        特别要注意的是，不可能向后走，找出这种均匀状态的初始下降位置，因为所有初始状态都会导致它。缺乏注入性使得一般情况下不可能倒退。

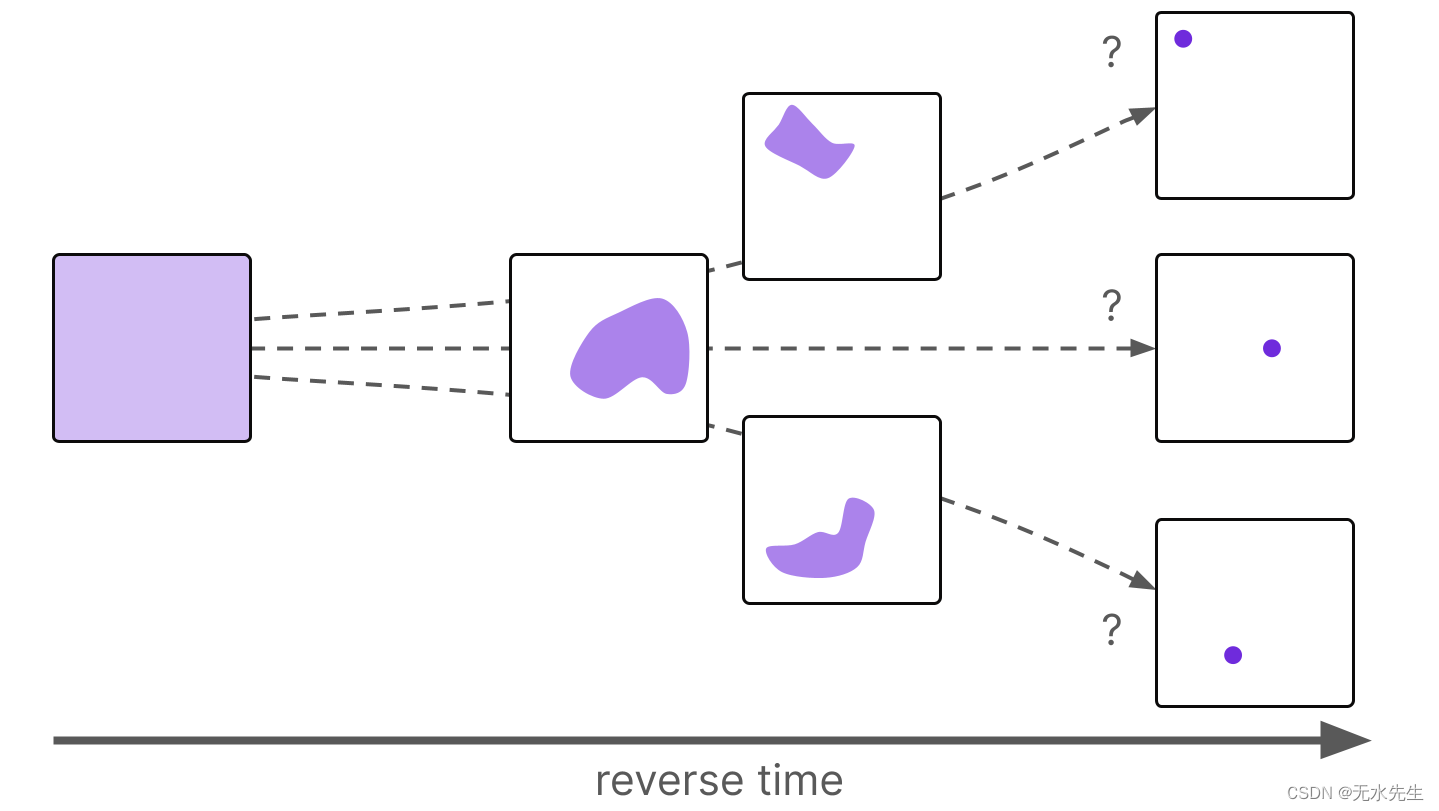
        由于所有可能的下降都会导致相同的最终状态，因此在仅查看最终状态时不可能知道初始下降的位置。

        我们总是知道液滴在正向时间内如何扩散，但由于注入性问题，我们不知道如何反向扩散均匀着色。但是，如果我们将关注点归结为一个特定的下降点，那么我们可以在时间上向前和向后模拟这个过程。

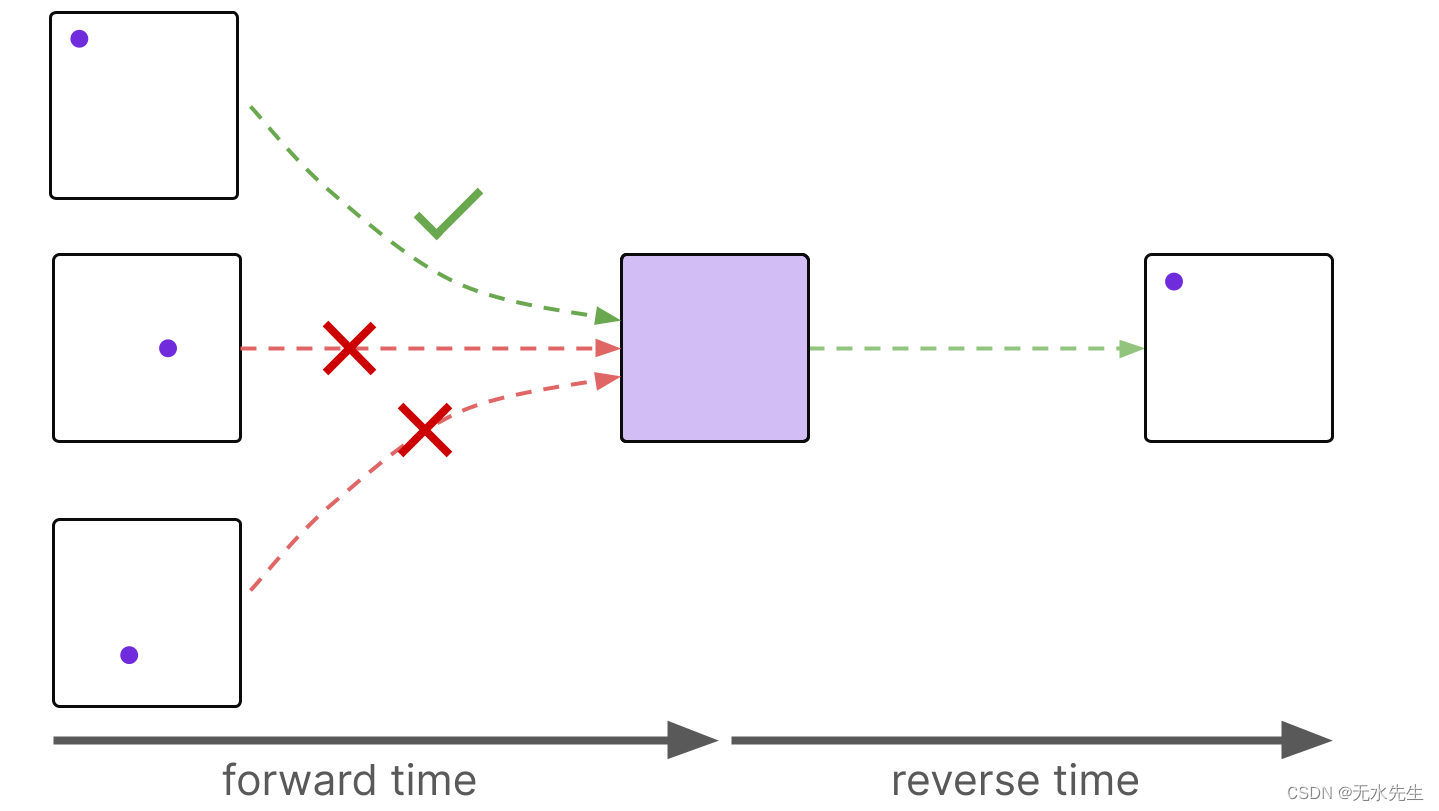
        如果我们只考虑一个初始滴点位置，那么我们可以成功地模拟随时间向前和向后的扩散过程

        扩散模型在图像域中使用相同的原理。特别是，扩散模型的不同“液滴”对应于不同类型的图像。例如，这些水滴可以对应于狗的图像、人类的图像和手写数字的图像。

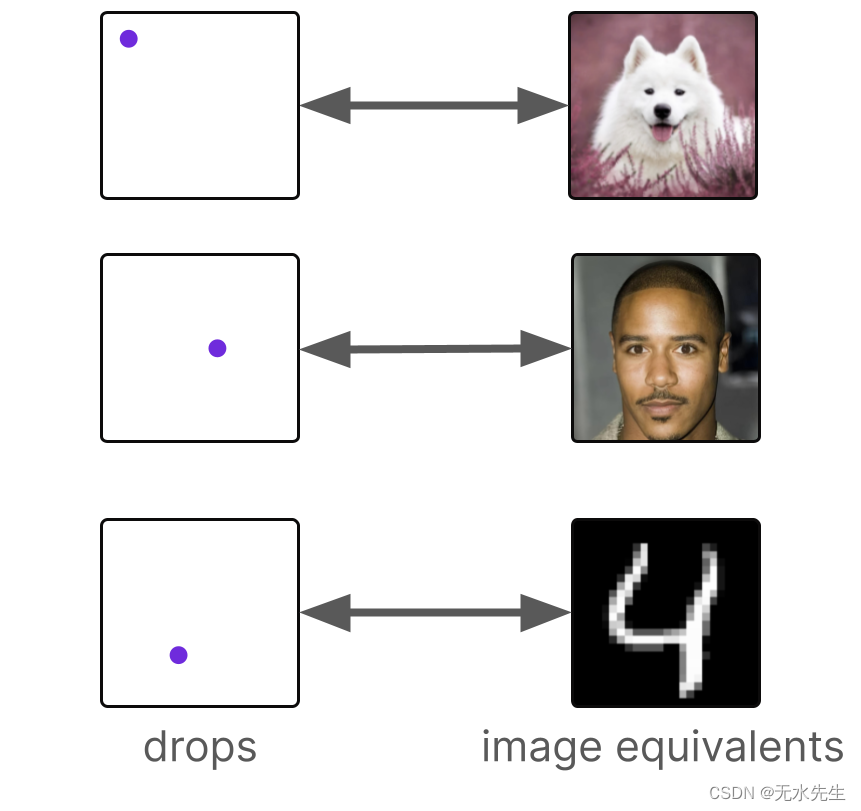
每种类型的图像（狗脸、人脸、数字）都类似于液体中不同的初始“滴”

        通过只选择一种类型的图像，比如狗的图像，扩散模型可以学会为这种类型的图像及时倒退，就像我们如何通过只选择一滴来学习从统一的颜色中倒退一样。

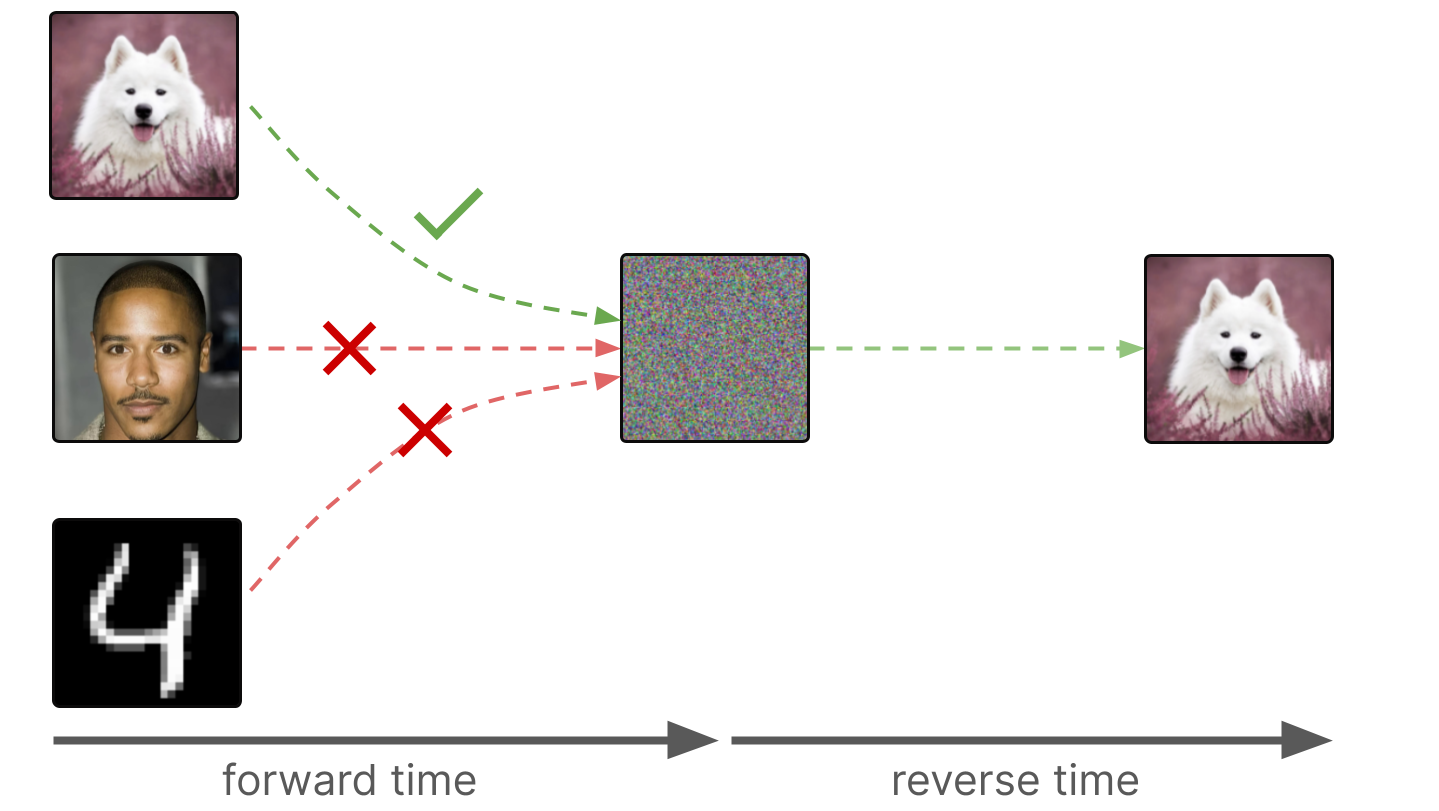
通过只选择一种类型的图像，在本例中为狗的图像，我们可以学会从电视静态到狗的图像的时间倒退

3.5 使用扩散模型生成图像

        可能还不清楚我们为什么要这样做——如果我们有一个狗的图像数据集，我们为什么要像这样前进和后退？答案在于，正上方的图略带欺骗性——狗的特定图像与食用色素的滴度不同——它是狗的整个类别的图像类似于食用色素的滴落。

        狗的特定图像实际上类似于食用色素滴中的特定原子。从上面回想一下，将我们的关注点归结为最初的一滴，使我们能够在时间上向前和向后模拟扩散过程。

        从上面，我们看到，专注于一个特定的起始落点可以让我们对正向和反向时间的动态进行建模

        了解扩散过程在逆时中是如何工作的，使我们能够将单个原子追溯到它们在液滴中的起点。特别是，我们从均匀的食用色素中随机挑选一个原子，然后逆转时间，看看它从哪里开始。

        选择一滴可以让我们在相反的时间内模拟扩散，这使我们能够将单个原子追溯到它们的起始位置

        我们用扩散模型来模拟这个过程。类似地，我们随机选择一张电视静态图像（“原子”），然后通过时间倒流来找出它在数据分布中的起点（“初始下降”）。也就是说，我们确定哪个狗的图像导致了该电视静态图像。

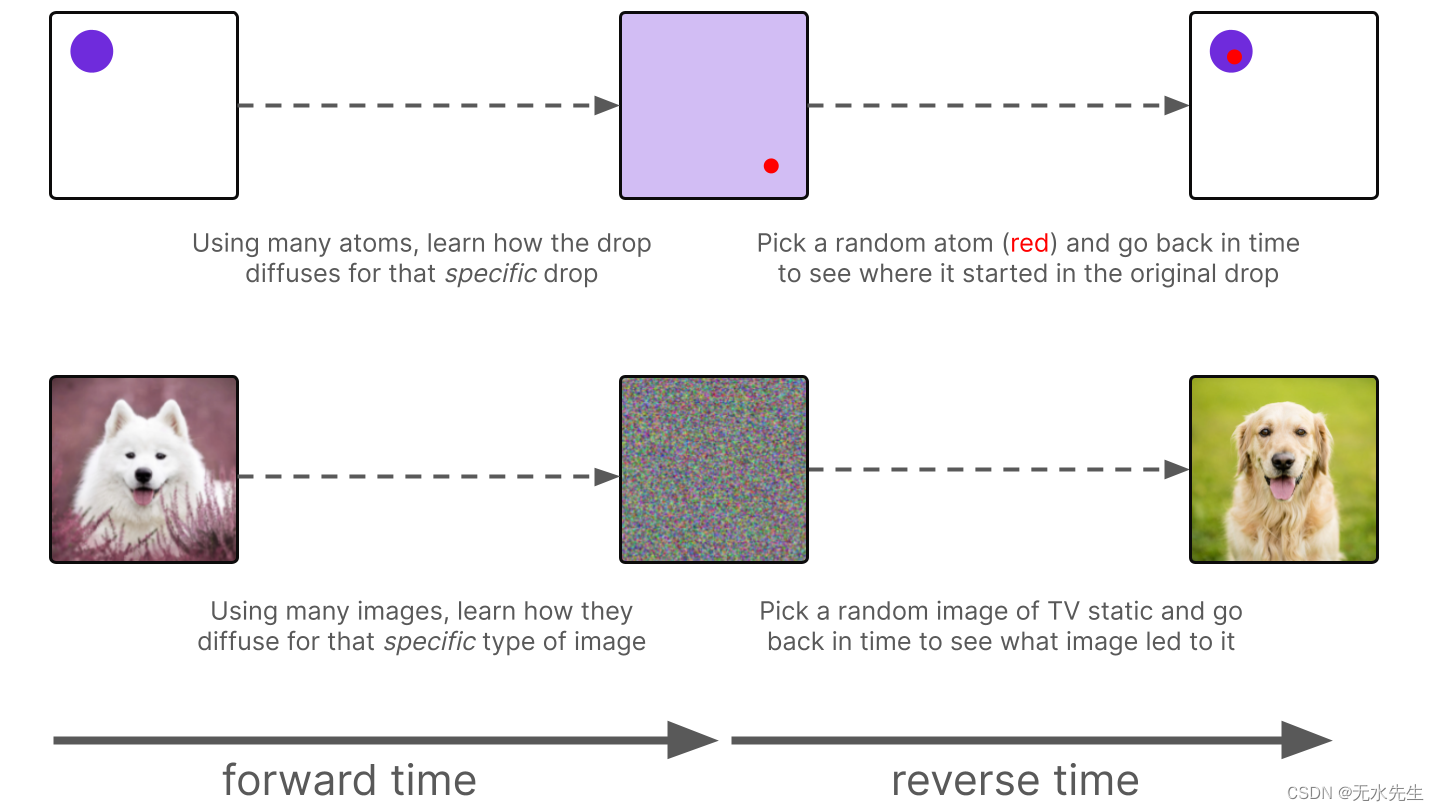
        图像就像原子 - 我们使用一组特定类型（例如狗）的示例（训练数据）来了解扩散过程如何适用于该类型的任何特定图像。然后，我们随机选择一张电视静态图像（不在训练数据中），并利用这些知识生成新颖的图像。

        这个过程与PFGM非常相似。借助 PFGM，我们对将数据分布映射到均匀半球的物理场进行了建模。由于半球很容易采样，我们在上面选择一个点，并在逆时运行物理场以生成新图像。通过扩散模型，我们对将数据分布映射到电视静态的物理场进行建模。由于电视静态很容易生成，因此我们随机选择一张电视静态图像，并在逆时运行物理以生成新图像。

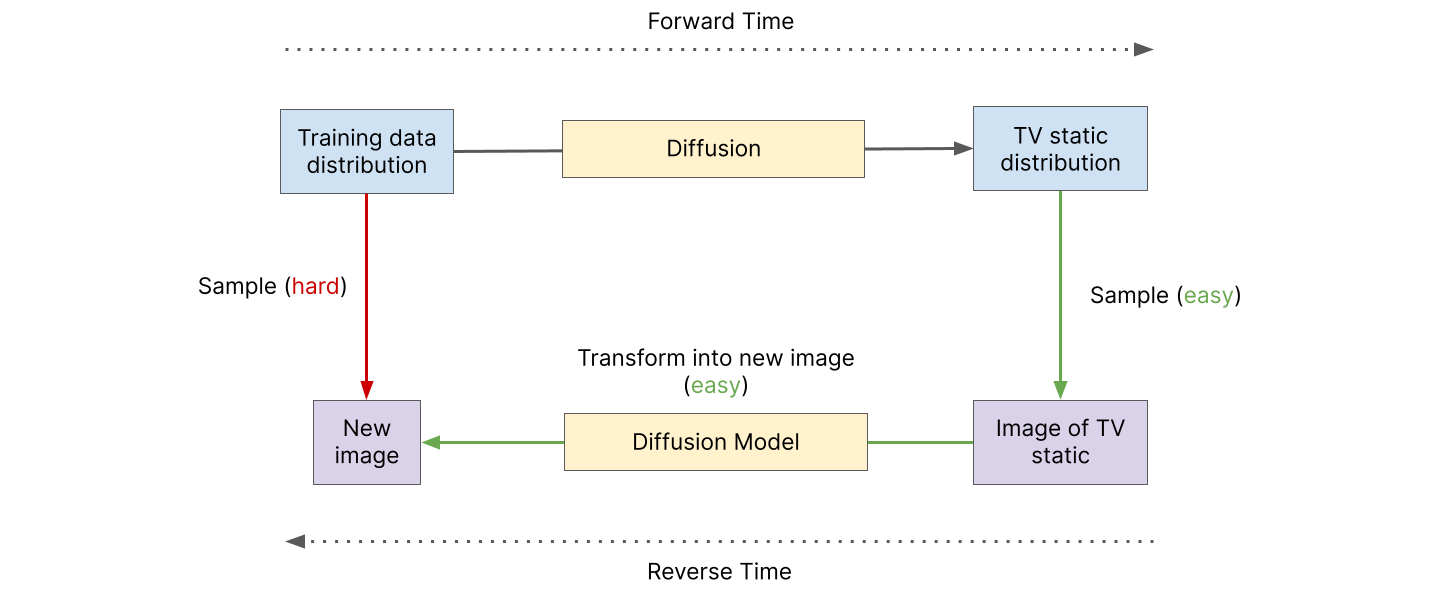
从数据分布中采样是困难的，但从电视静态分布中采样则不然。注意到物理学将前者转化为后者，我们使用反时间物理学将后者的样本转换为前者的样本。

扩散模型是生成式人工智能在图像领域取得很大进展的基础。像 Imagen 和 DALL-E 2 这样的文本到图像模型增强了这一过程，使我们能够告诉模型我们希望生成的图像是什么样子。

四、最后的话

        人工智能的许多最新进展都受到物理学思想的启发。正如我们所看到的，这些高级思想是生成式人工智能现代方法的基础，为最新一代的人工智能模型提供动力。

        如果您喜欢这篇文章，请随时查看我们的其他一些文章，以了解大型语言模型的涌现能力或 ChatGPT 的实际工作原理。或者，请随时订阅我们的时事通讯，以便在我们发布此类新内容时随时了解情况。