一、集成学习

1、传统学习的问题

传统学习面临的问题：没有任何情况下都最好的机器学习算法

2、集成学习

1）背景

通过将多个学习器进行集成，常可获得比单一学习器显著优越的泛化性能，这对弱学习器尤为明显。

弱学习器：准确率仅比随机猜测略高的学习器。
强学习器：准确率高并能在多项式时间内完成的学习器。

2）概念

通过构建并结合多个学习器完成学习任务
也称为多分类器系统(Multi-Classifier System)、基于委员会的学习(Committee based Learning)

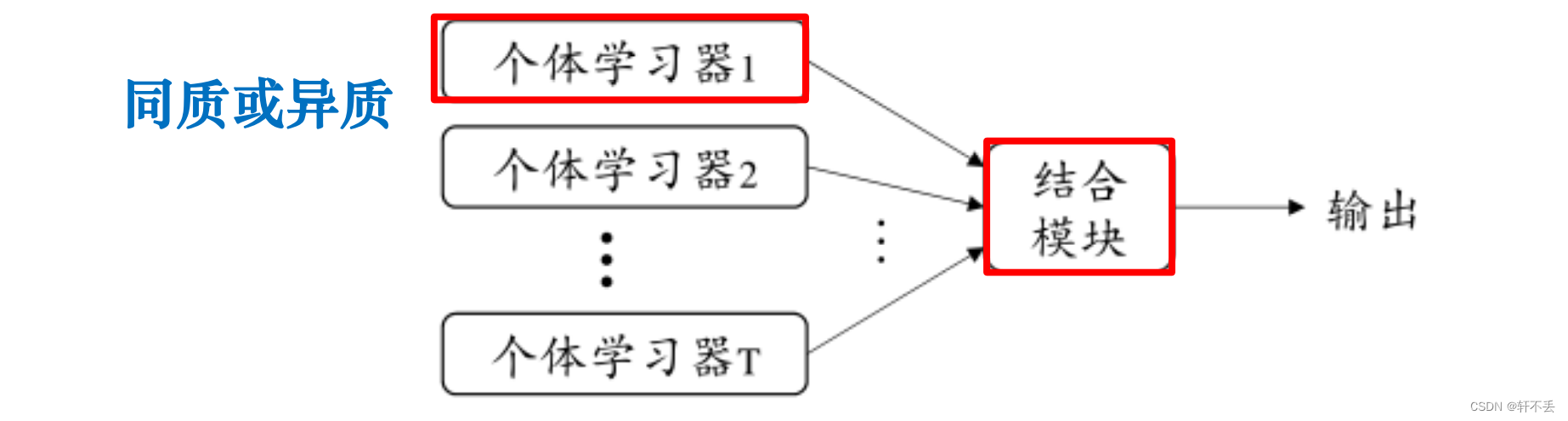
3）注意

多个学习器不一定比单一学习器性能好

由定理可知，在一定条件下，随着集成分类器数目的增加，集成的错误率将指数级下降，最终趋向于0

3、多样性度量

– 用于度量集成中个体学习器的多样性
– 考虑个体学习器的两两相似/不相似性

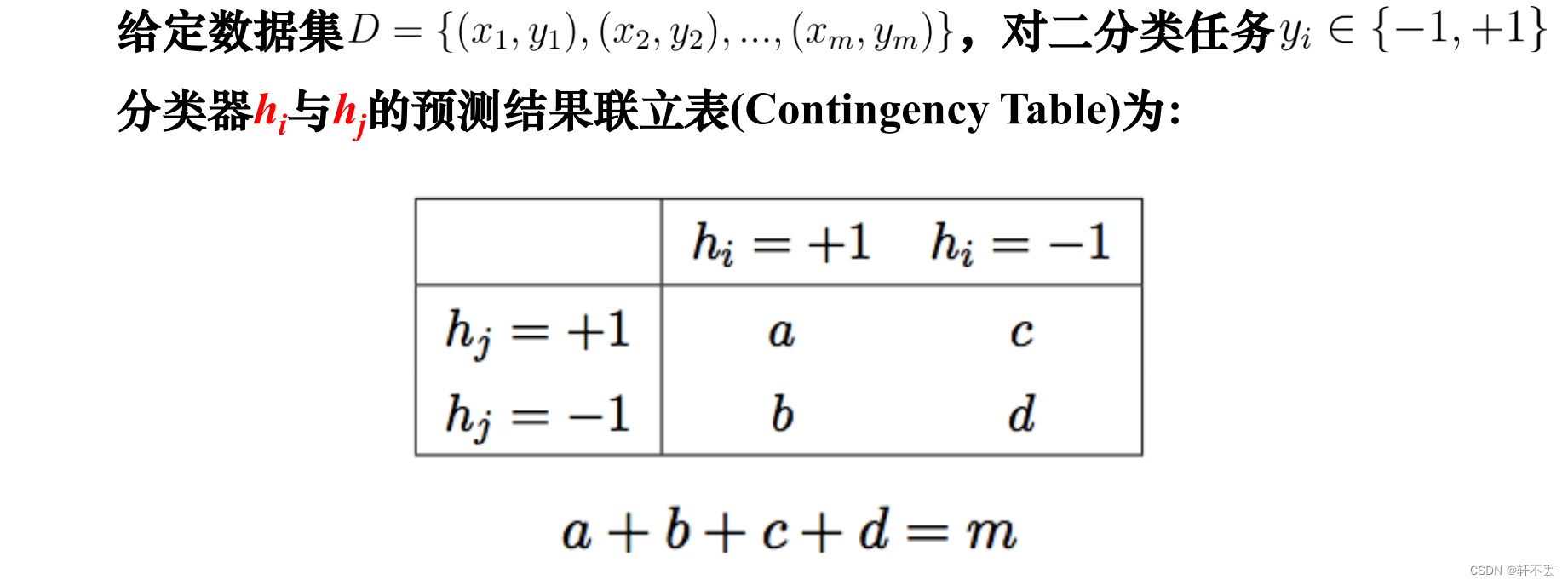
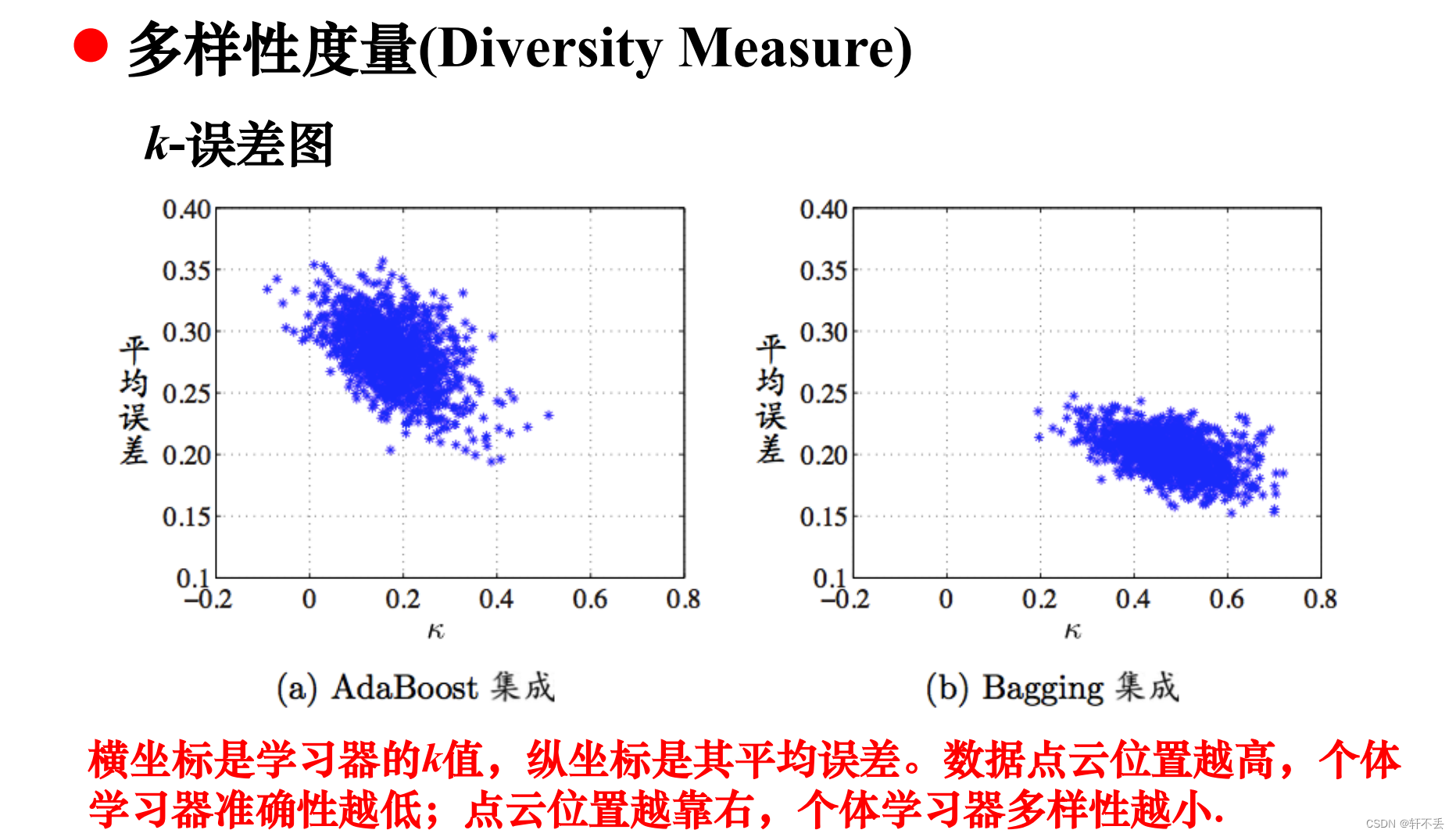
4、多样性增强

1）多样性增强：在学习过程引入随机性

– 数据样本扰动
    • Bagging中的自助采样
    • Adaboost中的序列采样
    – 对数据样本扰动敏感的基学习器(不稳定基学习器) 效果明显
    （决策树，神经网络等）
    – 对数据样本扰动不敏感的基学习器(稳定基学习器)效果不明显
     （线性学习器，支持向量机，朴素贝叶斯，K近邻等）

2） 输入属性扰动

不同子空间提供观察数据的不同视角

对包含大量冗余属性数据，可产生多样性大的个体学习器，还因属性数减少会大幅节省时间开销；若数据只含少量属性或冗余属性较少，则不宜使用

3） 输出表示扰动

在学习过程引入随机性

4） 算法参数扰动

随机设置不同的参数或环节。
单一学习器利用交叉验证对参数寻优，事实上相当于使用了不同参数训练学习器，最后仅选择了一个；而集成学习相当于把所有学习器都利用起来

– Adaboost：加入了数据样本扰动
– 随机森林：同时加入了数据样本扰动和输入属性扰动

5、集合策略

1）平均法

数值型输出最常见的结合策略

加权平均法是集成学习的基本出发点，各种结合方法都可视为其特例或变体，不同的集成学习方法是通过不同的方式确定加权平均法中基学习器的权重

2）投票法

标签型输出最常见的结合策略

3）学习法

当训练数据很多时采用另一个学习器进行结合

二、集成学习方法

根据个体学习器生成方式不同，形成两大类方法

1、串行化方法

条件：个体学习器间存在强依赖关系

1）典型算法：提升Boosting算法(Adaboost)

– 重赋权法(Re-weighting)：在每轮根据样本分布为每个训练样本重新赋予权重
– 重采样法(Re-sampling)：在每轮根据样本分布对训练集重新采样形成新的训练集

1. 先从初始数据集训练一个基学习器
2. 再根据其对训练样本分布（权重）进行调整，使先前错分样本在后续受到更多关注
3. 基于调整后的样本分布训练下一个基学习器；
4. 重复进行直至基学习器数目达到预先指定值；最终将这些基学习器加权结合

2）特点总结

1. 基本思想是用贪心法最小化损失函数，
2. 主要关注降低偏差：顺序串行地最小化损失函数，基于弱学习器逐步构造出很强的集成学习器，bias自然逐步下降
3. 但是由于模型的相关性很强，因此不能显著降低方差
4. 所以boosting主要靠降低bias来提升预测精度
5. Boosting中每个模型是弱模型，偏差高，方差低

2、并行化方法

条件：个体学习器间不存在强依赖关系

1）典型算法：Bagging算法

1. 利用自助法采样(Bootstrap Sampling)可构造T个含m个训练样本的采样集，基于每个采样集训练出一个基学习器，再将它们进行结合
2. 在对预测输出结合时，通常对分类任务使用简单投票法，对回归任务使用简单平均法
   

2）算法特点

1. 时间复杂度低：集成与直接训练一个学习器复杂度同阶
   假定基学习器的计算复杂度为$O(m)$，采样与投票/平均过程的复杂度为$O(s)$，则$Bagging$的复杂度大致为$T(O(m)+O(s))$；
2. 可以直接用于多分类、回归等任务；
3. 可包外估计(Out-of-Bag Estimate)泛化性能

3）特点总结

1. 主要关注降低方差，即通过多次重复训练提高稳定性，在易受样本扰动的学习器上效用更为明显(如不剪枝的决策树、神经网络等)
2. 在Bagging中，每个模型的偏差方差近似相同，但是互相相关性不太高，因此一般不能降低偏差
3. Bagging中的模型是强模型，偏差低，方差高

4）典型算法：随机森林算法

Bagging方法的一种扩展变体。以决策树为基学习器。
– 数据集的随机选择：自助采样法
– 待选属性的随机选择：对基决策树的每个结点，先从该结点的($d$个)属性集合中随机选择一个包含 $k$ 个属性的子集，再从这个子集选择一个最优属性用于划分, 一般情况下推荐 $k=lo{g}_{2}d$

5）算法流程

– 从原始数据集中每次随机有放回抽样选取与原始数据集相同数量的样本数据，构造数据子集；

– 每个数据子集从所有待选择的特征中随机选取一定数量的最优特征作为决策树的输入特征；

– 根据每个子集分别得到每棵决策树，由多棵决策树共同组成随机森林；

– 最后如果是分类问题，则按照投票的方式选取票数最多的类作为结果返回；如果是回归问题，则按照平均法选取所有决策树预测的平均值作为结果返回

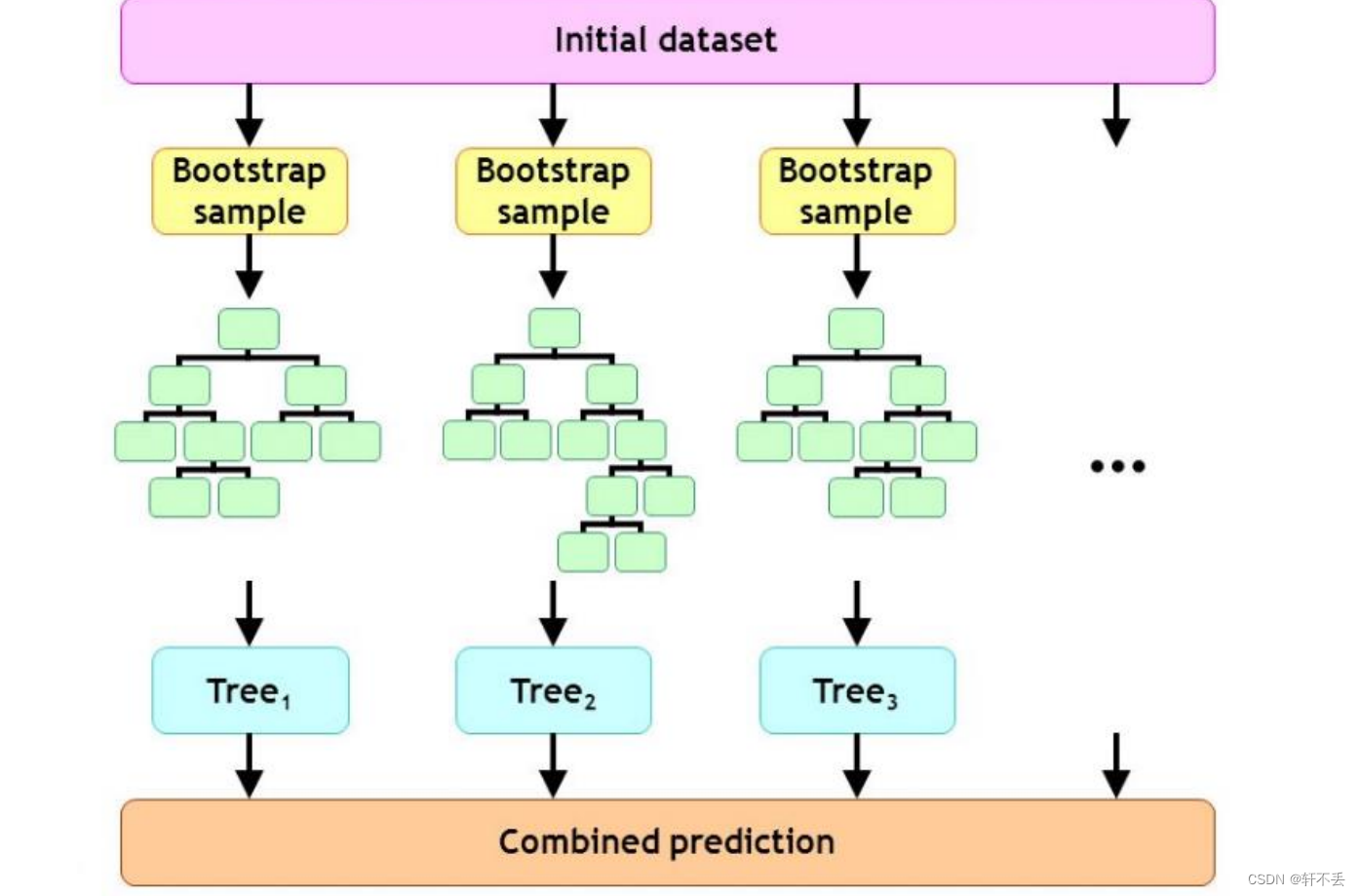
6）算法特点

– 基学习器多样性通过样本扰动和属性扰动实现
– 算法简单、容易实现、计算开销小
– 性能强大，被誉为“代表集成学习技术水平的方法”