决策树：理解机器学习中的关键算法
决策树是一种流行而强大的机器学习算法，它从数据中学习并模拟决策过程，以便对新的未知数据做出预测。由于其直观性和易理解性，决策树成为了分类和回归任务中的首选算法之一。在本文中，我们将深入探讨决策树的工作原理、如何构建决策树、它们的优缺点，以及在现实世界中的应用。
树模型
决策树：从根节点开始一步步走到叶子节点（决策）
所有的数据最终都会落到叶子节点，既可以做分类也可以做回归
例子：一个家庭里面找出玩游戏的人（通过年龄和性别两个特征）
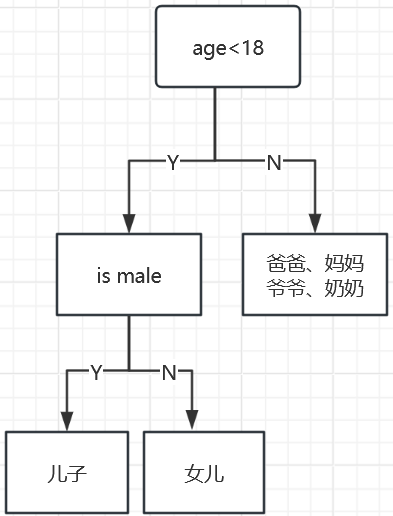
如何切分特征（选择节点）
问题：根节点的特征该用哪个特征？如何切分？
假设：我们目标应该是根节点就像一个老大一样能够更好的切分数据（分类的效果更好），根节点下面的节点自然就是二当家。
目标：通过一种衡量指标，来计算通过不同特征进行分支选择后的分类情况，找出最好的那个当成根节点，以此类推。
衡量指标——熵
熵：表示随机变量不确定性的度量（说白了就是物体内部的混乱程度，（概率越大）熵的值越小，物体的混乱程度越低，（概率越小）熵值越大，物体的混乱程度越高）
公式：
[ H(S) = -\sum_{i=1}^{n} p_i \log_2(p_i) ]
其中H（X）表示熵值大小
Pi表示：i在所有元素中的个数 / 元素总数
i:
例子：
A集合：【1，1，1，1，1，1，2，2，2，2】
B集合：【1，2，3，4，5，6，7，8，9，10】
A：负五分之三乘以二为底二分之一的对数减五分之二乘以二为底二分之一的对数
B：负十分之一乘以二为底十分之一的对数 再乘十
树的组成
根节点：第一个选择点
非叶子节点与分支：中间过程
叶子节点：最终的决策过程
决策树的基本原理
决策树通过一系列问题将数据集分割成越来越小的子集，最终达到一个可以做出预测的点。每个问题都基于特征和特征值，并且将数据集分割成两个或更多的同质子集，这些子集在目标变量上具有更高的纯度。
构建决策树的步骤
-
选择最佳特征：选择最佳分割特征是通过计算每个特征的信息增益（Information Gain）或基尼不纯度（Gini Impurity）来决定的。
-
分割数据：使用上一步选定的特征，将数据集分割成子集。分割可以基于一个阈值（用于连续特征）或特征的分类。
-
重复分割过程：在每个子集上重复步骤1和步骤2，直到每个子集达到一个停止标准（比如所有的记录都属于同一个类别，或者达到了树的最大深度）。
-
剪枝：为了避免过拟合，通过剪掉那些对模型预测能力提升不大的分支来简化决策树。
决策树的优点
-
直观易懂：决策树的结构清晰，易于理解和解释，它们的决策规则可以直观地展示出来。
-
不需要很多数据预处理：不需要标准化或归一化数据，也不需要处理缺失值。
-
可以处理非线性关系：由于分割过程的非参数性质，决策树能够捕捉到数据中的非线性关系。
-
多功能性：既可以处理分类问题，也可以处理回归问题。
决策树的缺点
-
容易过拟合：决策树可能会创建过于复杂的树结构，完美地匹配训练数据，但对新数据的泛化能力差。
-
稳定性较差：小的数据变动可能导致生成完全不同的树。
-
偏向于多类别的特征：使用信息增益作为分割标准时，决策树倾向于选择那些具有更多类别的特征。
应用实例
决策树广泛应用于各种领域，如医疗诊断、信用评分、股票市场分析、农业研究等。它们的直观性使得非专业人士也能够理解模型的预测结果。
结论
决策树由于其简单和有效性，在解决分类和回归问题上是一个不可或缺的工具。虽然单独的决策树可能容易过拟合，但通过组合多个决策树构成的集成方法，如随机森林和梯度提升决策树，可以大大提高模型的准确性和鲁棒性。学习和掌握决策树不仅有助于理解基本的机器学习原理，还为进一步探索更复杂的算法奠定了基础。
)
