RoPE位置编码是大模型中最常见的位置编码之一。像是谷歌的PaLM和meta的LLaMA等开源大模型都是RoPE位置编码,那么RoPE有什么特点呢?
本文将介绍如下内容:
- RoPE旋转位置编码概要
- 什么是位置编码?
- RoPE及其特点
- 总结
一、RoPE旋转位置编码概要
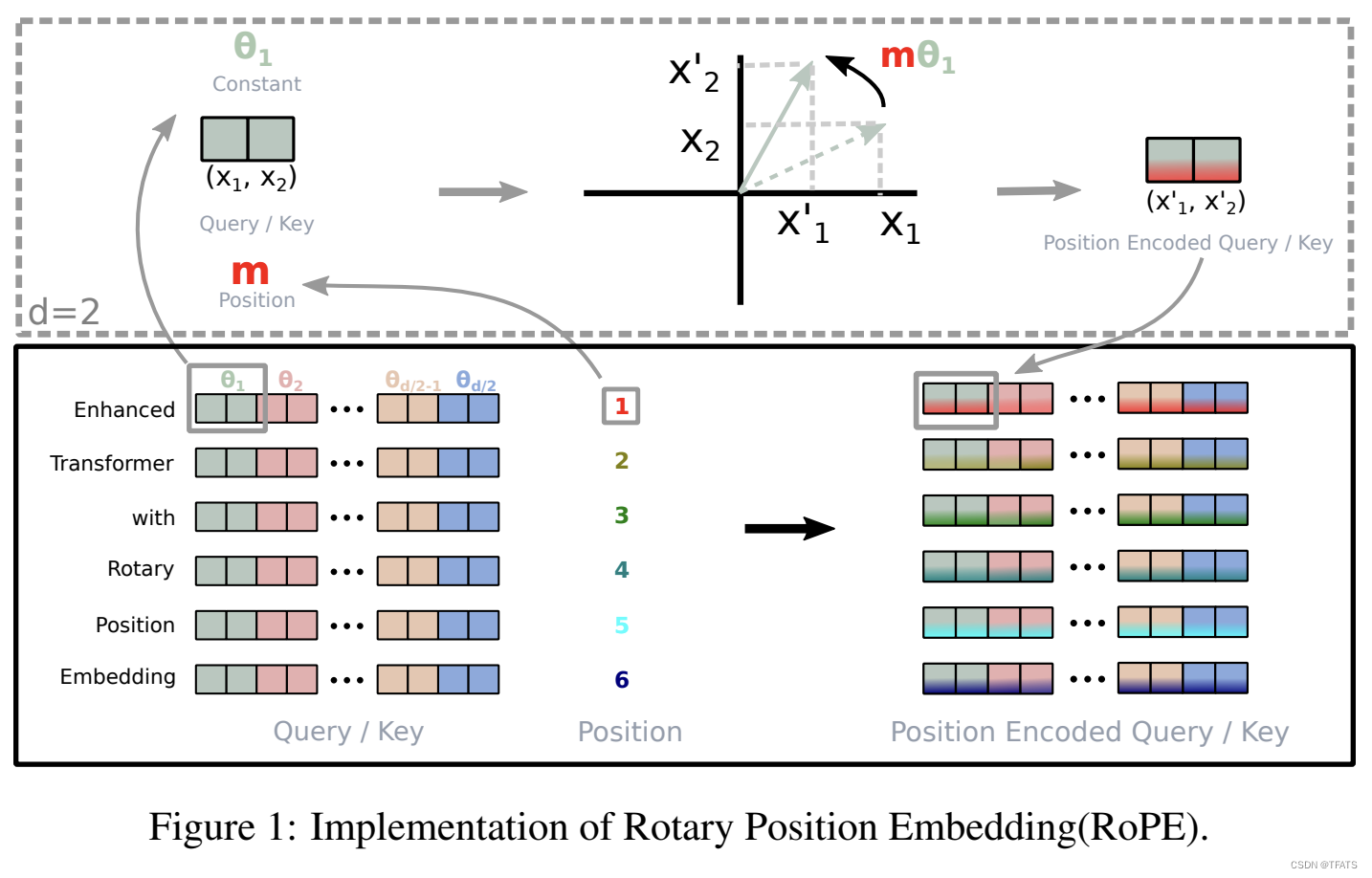
本文提出RoPE旋转位置编码方式,其关键思想是将上下文token表示和仅与位置相关的旋转矩阵相乘。RoPE具有良好的外推性和远程衰减的特性,应用到Transformer中体现出较好的处理长文本的能力。此外,RoPE还是目前唯一一种可用于线性Attention的相对位置编码。
中文原文:Transformer升级之路:2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces
代码地址:https://github.com/ZhuiyiTechnology/roformer
论文地址: ROFORMER: ENHANCED TRANSFORMER WITH ROTARY
POSITION EMBEDDING
二、什么是位置编码?
我们知道句子中不同词语之前的位置信息十分重要,但是self-attention框架无法直接利用位置信息,因此研究者提出了许多方法将位置信息编码到学习过程中。一是绝对位置编码方法,将位置信息直接加入到输入中;二是相对位置编码方法,研究者通过微调attention的结构,使它具有识别token位置信息的能力。
1、绝对位置编码
绝对位置编码比较简单,研究者一般会将绝对位置信息加到输入中:在输入的第 k k k个向量 x k x_k xk中加入位置向量 p k p_k pk得到 x k + p k x_k+p_k xk+pk,其中 p k p_k pk仅与 k k k相关 。计算 p k p_k pk的方法一般有两种:
训练式:将位置向量设置为可训练的参数,如Bert就将位置向量初始化设为512×768的矩阵,并在训练中更新。但是这种方法有个明显的缺点就是不具备外推性,如果预训练时句子最长设为512,它就无法处理更长的句子了。
编码式:最著名的就是《Attention is all you need》中提出的Sinusoidal位置编码(如下所示, p i , 2 t p_i,2t pi,2t表示位置 k k k的向量的第 2 i 2i 2i个分量, d d d表示向量维度),它显式的编码了位置信息,且具有一定的外推性。
2、相对位置编码
我们前面讲到相对位置编码是微调Attention矩阵的计算方式,先看看绝对位置编码怎样计算Attention矩阵:
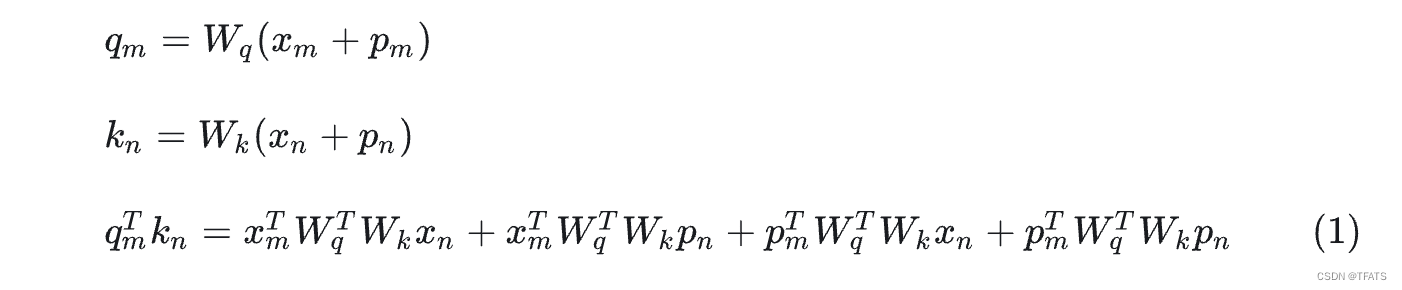
可以看到计算attention矩阵的过程如公式(1)所示,其中第一项和位置信息无关,第二至四项和位置信息相关。因此研究者通常是直接修改第二至四项的内容,直接在attention矩阵中添加相对位置信息。 常见的有以下几种方法:
XLNET式: 如(2)所示,xlnet将(1)中的二至四项都做了改变,具体的将 p n p_n pn替换为了Sinusoidal生成式编码 R ~ n − m \tilde{\mathbb{R}}_{n-m} R~n−m,将 p m p_m pm换成了两个可以训练的向量 u , v u,v u,v 。
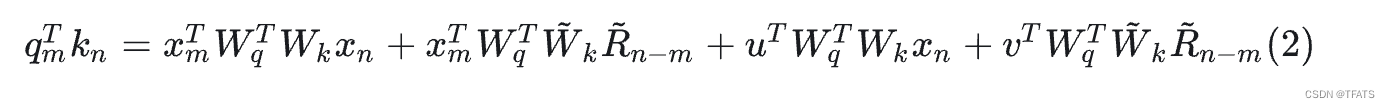
T5式: 如(3)所示,它的作者认为输入和位置间不应过多的交互,因此将第二、三项删除,将第四项都替换为一个可学习的偏执 b m , n b_{m,n} bm,n,这仅仅是在Attention矩阵的基础上加一个可训练的偏置项而已,十分简单。
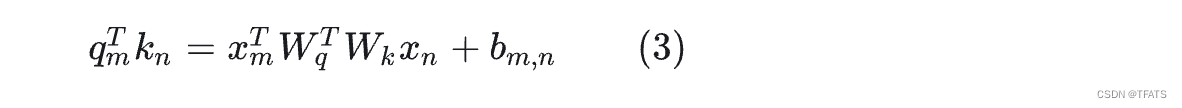
DeBerta式: 和T5的构造相反,它舍弃了公式(1)中第四项,保留了第二、三项并将位置信息替换为了相对位置向量 R ~ n − m \tilde{\mathbb{R}}_{n-m} R~n−m
。
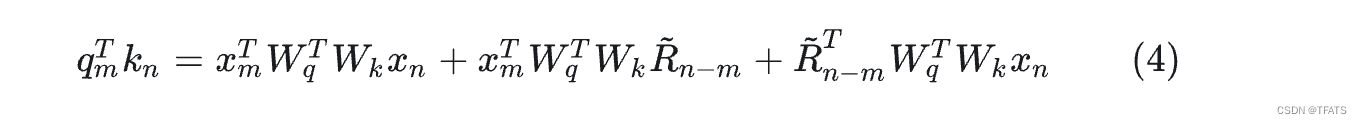
三、RoPE及其特点
Attention的核心运算是内积,所以我们希望经过内积的结果能够带有相对信息。那么我们希望
q m q_m qm和 k n k_n kn 的内积仅与输入 x m x_m xm, x n x_n xn和他们的相对位置 m − n m-n m−n有关,那么我们可以假设存在函数 g g g,使得:

1、RoPE的表示形式
为了方便理解我们可以先考虑二维形式,然后借助复数的运算法则来理解。首先分别用复数的指数形式表示各个向量变化,即有:
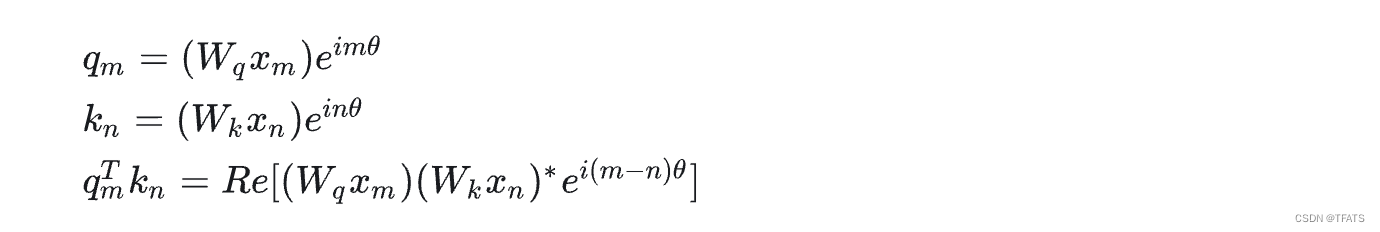
PS1. 向量内积与复数乘积的关系为内积 < i , j > = R e ( i j ∗ ) <i,j>=Re(ij*) <i,j>=Re(ij∗),其中 R e Re Re表示复数的实部。
PS2. 这个形式证明过程可以参考论文的3.4.1节。但是要注意的是向量内积是标量,而 g ( x m , x n , m − n ) g(x_m,x_n,m-n) g(xm,xn,m−n)是向量,所以其公式(21) 应改为 q m T k n = < f q ( x , m ) , f k ( m , n ) > = R e [ ( x m , x n . m − n ) ] q^{T}_mk_n=<f_q(x,m),f_k(m,n)>=Re[(x_m,x_n.m-n)] qmTkn=<fq(x,m),fk(m,n)>=Re[(xm,xn.m−n)],这样公式(24)才好理解。
以 q m q_m qm为例,假设 e i m θ e^{im\theta} eimθ表示为模长为1的复数,根据复数乘法的几何意义, ( W q x m ) e i m θ (W_qx_m)e^{im\theta} (Wqxm)eimθ变换实际上对应着向量 W q x m W_qx_m Wqxm的旋转,所以我们称之为“旋转式位置编码”,它还可以写成矩阵形式:
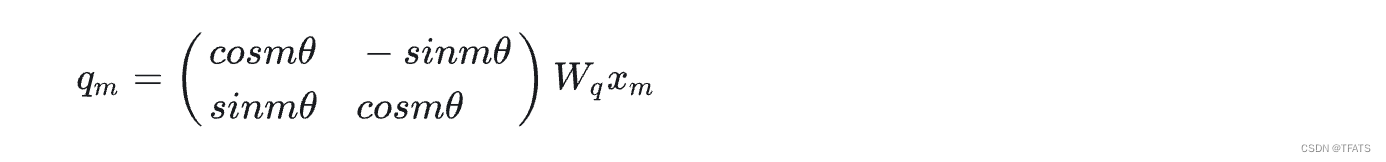
以 q m q_m qm为例,考虑多维情况,可以得到旋转式位置编码的一般形式为: q m = R Θ , m d W q x m q_m=R^d_{\Theta,m}W_qx_m qm=RΘ,mdWqxm ,其中:
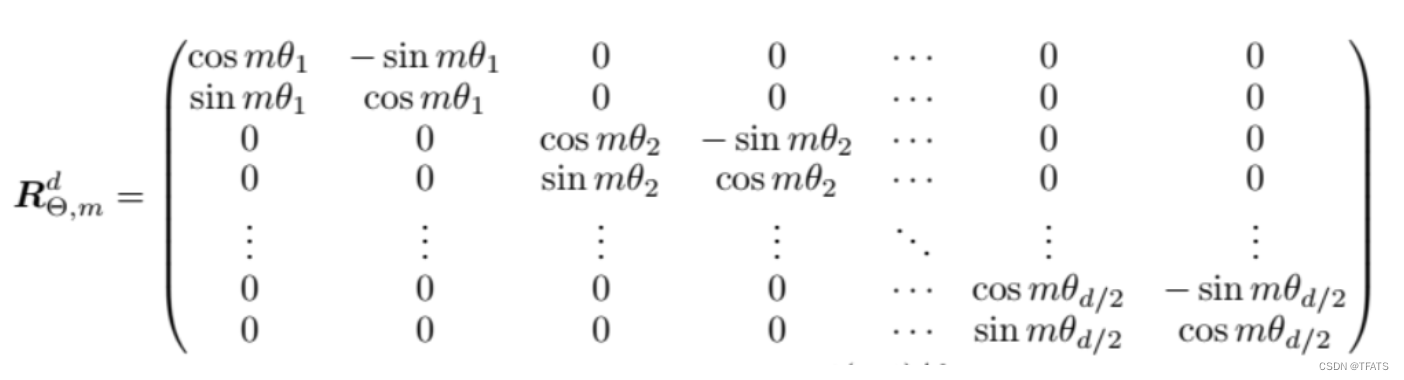
PS3. 矩阵 R Θ , m d R^d_{\Theta,m} RΘ,md为正交矩阵,它不会改变向量的模长,因此通常来说它不会改变原模型的稳定性。
2、RoPE的优点
-
远程衰减: 参考Sinusoidal位置编码形式,RoPE中将 θ i = 1000 0 − 2 i / d \theta_i=10000^{-2i/d} θi=10000−2i/d,作者并证明了RoPE具有远程衰减的优点,相对距离更大的token之间的联系更少。
-
可用于线性Attention:Attention的空间和时间复杂度都是 O ( n 2 ) O(n^2) O(n2)级别的, n n n是序列长度,所以 n n n当比较大时Transformer模型的计算量难以承受。因此有研究者提出了线性注意力机制,将复杂度将至 O ( n ) O(n) O(n)。线性注意力机制详见:线性Attention的探索:Attention必须有个Softmax吗? - 科学空间|Scientific Spaces。
线性注意力机制的表达式为:
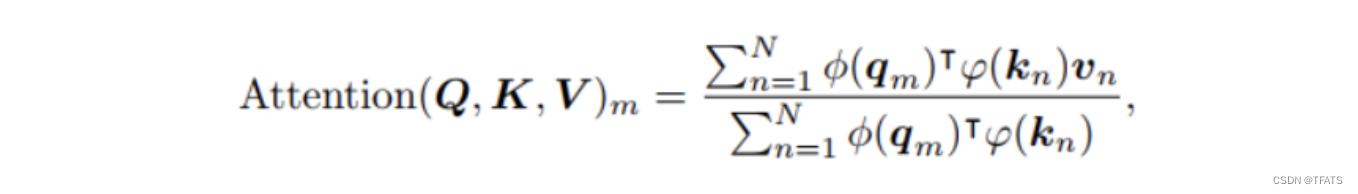
其中 φ ( ⋅ ) \varphi(\cdot) φ(⋅)为非负函数,像原生注意力中的softmax就位非负函数。因为线性Attention计算方式不一样了,所以前面提到的一些相对位置编码方式都不再适用。前面我们提到RoPE是通过旋转输入的方式添加位置信息,并不会改变各个参数的归一化值。因此,我们可以只在分子中将旋转矩阵乘以 φ ( ⋅ ) \varphi(\cdot) φ(⋅),即:
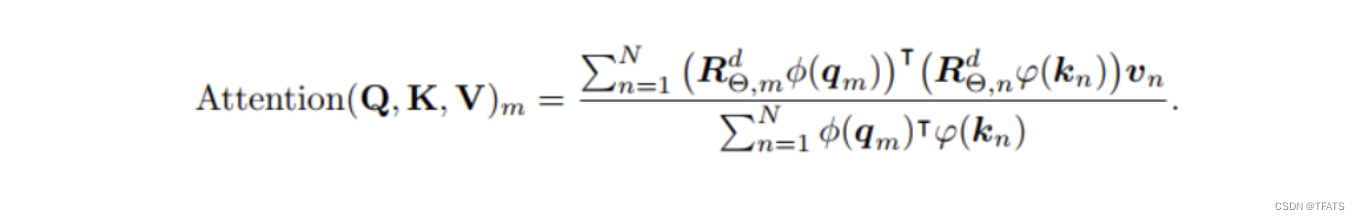
四、总结
本文作者详细梳理了位置编码的流派,提出了一种旋转位置编码方式RoPE,并从数学角度证明RoPE带来的诸多优点。RoPE能够应用于线性注意力中,这使得它在不引入爆炸计算量的前提下能够接受更长的输入,这可能是许多大模型都应用RoPE的原因。
参考:
【论文阅读】RoPE为何成为大模型中最常见的位置编码?
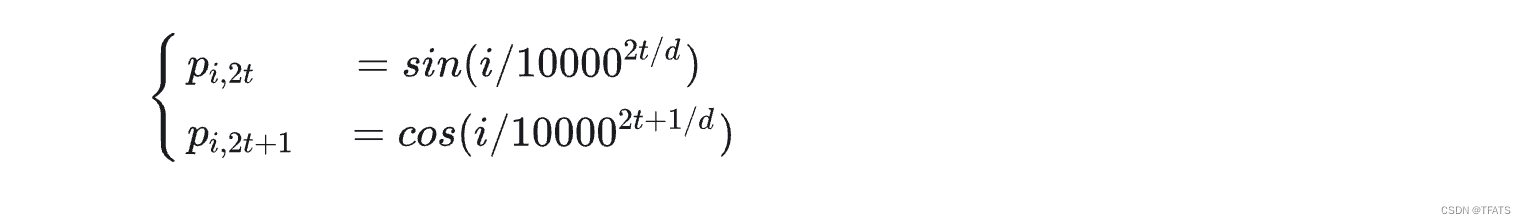


















)
