一、均方预测和随机序列分解
考虑随机序列
使用预测
定义
称为的均方可预测部分。
若相互独立,则
是均方不可预测的。
定义随机序列的新息序列
V(k)基于样本观测的条件均值为0,即均方不可预测。
V(k)与是正交的,即
。
二、卡尔曼滤波
输入观测量,对
进行估计得到
1. 系统模型
状态方程
观测方程
其中,
:状态向量,
:观测向量,
:状态噪声,
,高斯白噪声
:观测噪声,
,高斯白噪声
:状态转移矩阵,
:观测矩阵,
相关性质:
(1)乘积率:
(2)状态噪声自相关矩阵:
(3)观测噪声自相关矩阵:
(4)噪声独立性:
2. 新息过程
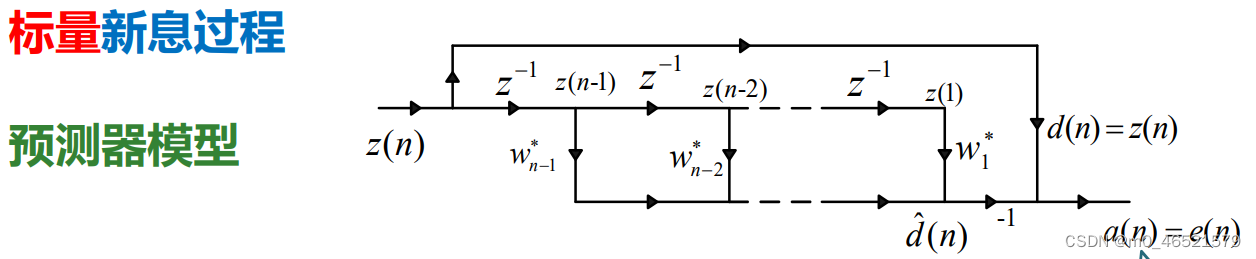
定义MMSE下的预测误差为新息过程,记作
记作
是用前n-1个观测值对z(n)进行MMSE估计。
其中,
观测向量:
权向量:
性质
(1)当前新息与以前各观测量正交
(2)当前新息与以前各新息正交
(3)新息与观测量等价

3. 用观测量估计(MMSE估计)状态变量
其中,
递推形式:
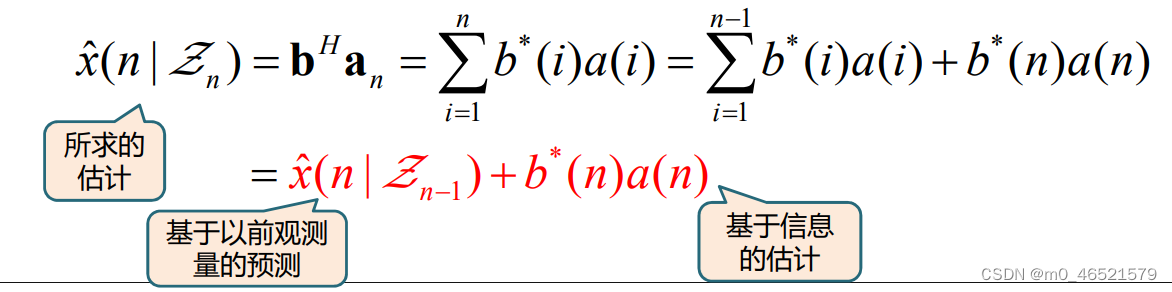


第2版 例3-4 CSS 立方体)





)

)




的模拟实现)
》)

