扰乱字符串
题目要求


解题思路
初步分析
给定两个字符串T和S,假设T是由S变换而来的
- 如果T和S长度不一样,必定不能变来
- 如果长度一样,顶层字符串S能够划分 S 1 S_1 S1和 S 2 S_2 S2,同样字符串T也能够划分为 T 1 T_1 T1和 T 2 T_2 T2
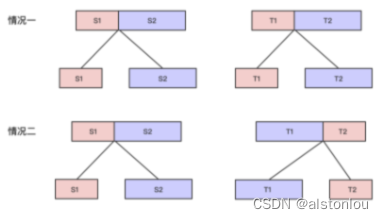
- 情况一:没交换, S 1 S_1 S1> T 1 T_1 T1, S 2 S_2 S2> T 2 T_2 T2
- 情况二:没交换, S 1 S_1 S1> T 2 T_2 T2, S 2 S_2 S2> T 1 T_1 T1
- 子问题就是分别讨论两种情况, T 1 T_1 T1是否由 S 1 S_1 S1变来, T 2 T_2 T2是否由 S 2 S_2 S2变来,或 T 1 T_1 T1是否由 S 2 S_2 S2变来, T 2 T_2 T2是否由 S 1 S_1 S1变来.
得到状态
dp[i][j][k][h]表示T[k…h]是否由S[i…j]变来。由于变换必须长度是一样的,因此这边有个关系 i - j = h - k,可以把四维数组降成三维。dp[i][j][len]表示从字符串S中i开始长度为len的字符串是否能变换为从字符串T中j开始长度为len的字符串
转移方程
dp[i][j][k]=- OR1<=w<=k-1{dp[i][j][k] && dp[i+w][j+w][k-w] }
- OR1<=w<=k-1 {dp[i][j+k-w][w] && dp[i+w][j][k-w]}
解释一下:枚举 S1长度 w(从 1~k-1,因为要划分),f[i][j][w]表示S1能变成T1,f[i+w][j+w][k−w]表示S2能变成T2,或者是S1能变成T2,S2能变成T1。
初始条件
对于长度为1的子串,只有相等才能变过去,相等为true,不等为false
代码
lens1=len(s1)lens2 = len(s2)if lens1 != lens2:return False# 初始化dp3维数组dp[i][j][k]# i为0~lens1-1共lens1个, j为0~lens1-1共lens1个, k为1~lens1+1共lens1个dp=[ [ [False]*(lens1+1) for _ in range(lens1) ] for _ in range(lens1)]#初始化单个字符的情况for i in range(lens1):for j in range(lens1):dp[i][j][1]= s1[i]==s2[j]#前面排除了s1和s2为单个字符的情况,那么我们就要划分区间了,k从2到lens1,也就是划分为s1[:k]和s1[k:]#枚举区间长度2~lens1for k in range(2,lens1+1):#枚举S中的起点位置for i in range( lens1-k+1):#也就是在s1中枚举i的位置,因为后面会出现i+w的情况,而w最大就是k,# 就会有i+k的情况,所以i的取值范围就是0~lens1-k#枚举T中的起点位置for j in range(lens1-k+1):#枚举划分位置,s1[:k]中从for w in range(1, k):#第一种情况:S1->T1,S2->T2if dp[i][j][w] and dp[i + w][j + w][k - w]:dp[i][j][k] = Trueprint("i,j,k", i, j, k)break#第二种情况:S1->T2,S2->T1#S1起点i,T2起点j + 前面那段长度k-w,S2起点i+前面长度kif dp[i][j + k - w][w] and dp[i + w][j][k - w]:dp[i][j][k] = Trueprint("i,j,k", i, j, k)breakreturn dp[0][0][lens1]
复杂度分析
时间复杂度: O ( N 3 ) O(N^3) O(N3)
空间复杂度: O ( N 4 ) O(N^4) O(N4)
其他解法
递归
这个题相当于让我们来判断两颗二叉树是否能通过翻转某些子树而相互得到。
思路:从一个位置将两个字符串分别划分为两个子串,然后递归判断两个字符串是否互相为[扰乱字符串]。
因为不知道在哪个位置分割字符串,所以直接遍历每个位置进行分割。在判断是否两个子串能否通过翻转变成相等的时候,需要保证传给函数的两个子串长度是相同的。
综上,因此分两个情况讨论:
S1[0:i]和S2[0:i]作为左子树,S1[i:N]和S2[i:N]作右子树S1[0:i]和S2[N-i:N]作为左子树,S1[i:N]和S2[0:N-i]作为右子树
其中左子树的两个字符串的长度都是i,右子树的两个字符串的长度都是N-i。如果上面两种情况由一种能够成立,则s1和s2是[扰乱字符串]
递归终止符号:当长度是0,长度是1时的两个字符串是否相等进行判断。如果两个字符串本身包含的字符就不等,那么一定不是[扰乱字符串],所以我们对两个字符串排序后,是否相等也进行判断。
记忆化递归
本题如果直接使用上面的递归方法解答,会超时,因为在不同的递归输入时,存在对相同子串的重复计算。避免重复计算的方式是使用[记忆化递归]。这个思路不难,就是把已经计算过的结果保存到缓存中,当此后再有同样的递归输入的时候,直接从缓存里面查,从而避免了重复计算。
在python中,有一个实现记忆化递归的神器,就是functool模块的lru_cache装饰器,它可以把函数的输入和输出结果缓存住,在后续调用中如果遇到了相同的输入,直接从缓存里面读取。顾名思义,它使用的是LRU(最近最少使用)的缓存淘汰策略。
@functools.lru_cache(maxsize=None, typed=False)
maxsize为最多缓存次数,如果为None,则无限制;typed = True时,表示不同参数类型的调用将分别缓存。
这装饰器使用方法很简单,看下面代码的第二行。
代码:
class Solution:@functools.lru_cache(None)def isScramble(self, s1: str, s2: str) -> bool:N = len(s1)if N == 0: return Trueif N == 1: return s1 == s2if sorted(s1) != sorted(s2):return Falsefor i in range(1, N):if self.isScramble(s1[:i], s2[:i]) and self.isScramble(s1[i:], s2[i:]):return Trueelif self.isScramble(s1[:i], s2[-i:]) and self.isScramble(s1[i:], s2[:-i]):return Truereturn False复杂度分析
时间复杂度: O ( N ! ) O(N!) O(N!)
空间复杂度: O ( N ! ) O(N!) O(N!)
)








)
/经管类的期刊投稿指南)




)

)
到HDFS)
