三角剖分（Triangulation），对数值分析（比如有限元分析）以及图形学来说，都是极为重要的一项预处理技术。尤其是Delaunay三角剖分，由于其独特性，关于点集的很多种几何图都和Delaunay三角剖分相关，如Voronoi图，EMST树，Gabriel图等。Delaunay三角剖分有最大化最小角，“最接近于规则化的“的三角网和唯一性（任意四点不能共圆）两个特点。

Delaunay三角剖分

Delaunay三角剖分 定义

三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：1.除了端点，平面图中的边不包含点集中的任何点。2.没有相交边。3.平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。

是不是有点不好理解，那我接下来就通俗一点解释一下。
请看下图

这上面的蓝色小点就是上文所说二维实数的有限点集：V

下图任一连接的线段 就是 点集中的点作为端点构成的封闭线段：边e
那么所有封闭线段就是  Delaunay 边合集：E

Delaunay 边

Delaunay边：假设E中的一条边e（两个端点为a,b），e若满足下列条件，则称之为Delaunay边：存在一个圆经过a,b两点，圆内(注意是圆内，圆上最多三点共圆)不含点集V中任何其他的点，这一特性又称空圆特性。

Delaunay 空圆特性

什么叫空圆特性呢，简单来说：任意四点不能共圆。
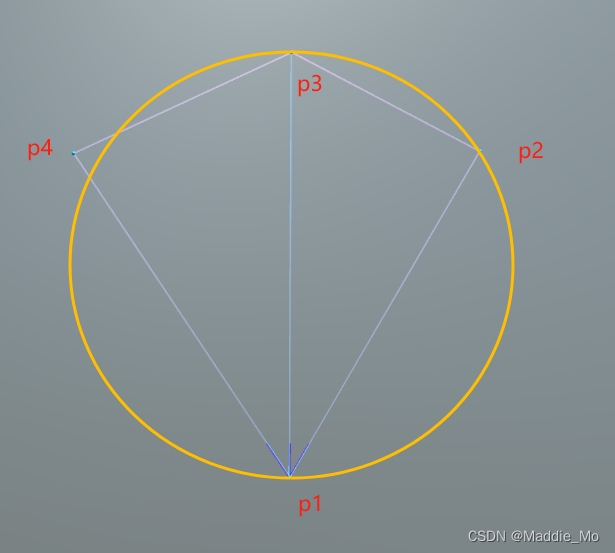
就是需要保证：在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在。以线段P13为直径画圆，发现点P1、P2、P3共圆，P4在当前圆外，满足空圆特性，所以线段P13为Delaunay边。
这里插一嘴其实P24 也满足Delaunay边空圆特性，为什么没有使用呢，这就要说到Delaunay 的另一个特点了。
《最大化最小角特性》

Delaunay 三角形

Delaunay三角剖分：如果点集V的一个三角剖分T只包含Delaunay边，那么该三角剖分称为Delaunay三角剖分。

Delaunay 最大化最小角特性

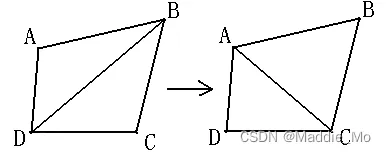
最大化最小角特性：在散点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。具体的说是指在两个相邻的三角形构成凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。

什么意思呢：就是要保证每个内角的最大化。
啧，再换个说话就是：最好是等边三角形。对对对  就是这样

Delaunay 三角形特征

Delaunay 三角形 具备的优异特性：1.最接近：以最近的三点形成三角形，且各线段(三角形的边)皆不相交。2.唯一性：不论从区域何处开始构建，最终都将得到一致的结果。3.最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小的角度不会变大。4.最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。5.区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。6.具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

废话不多说 直接上图

	1.最接近：以最近的三点形成三角形，且各线段(三角形的边)皆不相交。2.唯一性：不论从区域何处开始构建，最终都将得到一致的结果。

	3.最优性：任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小的角度不会变大。4.最规则：如果将三角网中的每个三角形的最小角进行升序排列，则Delaunay三角网的排列得到的数值最大。

有限点集 V  增加

	5.区域性：新增、删除、移动某一个顶点时只会影响临近的三角形。

	6.具有凸多边形的外壳：三角网最外层的边界形成一个凸多边形的外壳。

Delaunay 算法

不同情况选择不同的优化算法。Lawson算法：容易快速实现，执行迅速但是点集过大会造成卡顿问题。Bowyer-Watson算法：实现难度中等，执行逻辑会慢一点，但是比较完善，属于Lawson算法的优化版本。

Delaunay Lawson算法

逐点插入的Lawson算法是Lawson在1977年提出的，该算法思路简单，易于编程实现。基本原理为：首先建立一个大的三角形或多边形，把所有数据点包围起来，向其中插入一点，该点与包含它的三角形三个顶点相连，形成三个新的三角形，然后逐个对它们进行空外接圆检测，同时用Lawson设计的局部优化过程LOP进行优化，即通过交换对角线的方法来保证所形成的三角网为Delaunay三角网。上述基于散点的构网算法理论严密、唯一性好，网格满足空圆特性，较为理想。
由其逐点插入的构网过程可知，遇到非Delaunay边时，通过删除调整，可以构造形成新的Delaunay边。
在完成构网后，增加新点时，无需对所有的点进行重新构网，只需对新点的影响三角形范围进行局部联网，且局部联网的方法简单易行。同样，点的删除、移动也可快速动态地进行。但在实际应用当中，这种构网算法当点集较大时构网速度也较慢，如果点集范围是非凸区域或者存在内环，则会产生非法三角形。

当离散点集构成圆环时，Lawson算法产生的非法三角形

圆环状 离散点集

中间区域就是 Lawson算法产生的非法三角形网格。
当然你要是选择的是覆盖模式的话，他就是合法的。所以说算法没有好坏只有应用不同。

Delaunay Bowyer-Watson算法

Bowyer-Watson 算法是一种用于生成 Delaunay 三角剖分的算法。它是基于迭代的插入点的方法，逐步构建三角网格。

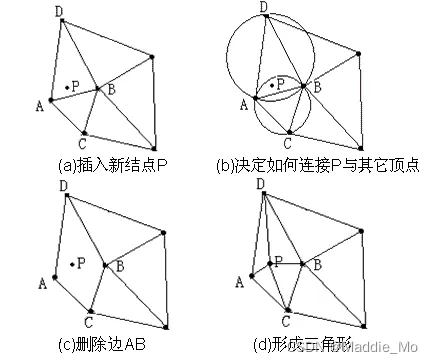
 Bowyer-Watson 算法的基本步骤：1.初始化：在算法开始之前，创建一个超级三角形，它包含所有要进行三角剖分的点。超级三角形的顶点选择应该是足够远离点集的范围，以确保所有的点都在超级三角形内。2.逐个插入点：对于每个要插入的点，执行以下步骤：a).找到包含该点的三角形（称为“外接三角形”）。b.从外接三角形中的顶点开始，以逆时针的方式遍历三角形的边。c).对于每条边，检查是否有一个以该边为边界的外接圆包含了插入点。d).如果存在这样的外接圆，说明当前三角形不是 Delaunay 三角形。将该三角形从三角网格中删除，并将插入点与边的另一个顶点形成两个新的三角形。e).如果不存在这样的外接圆，说明当前三角形是 Delaunay 三角形。将插入点与当前三角形的三个顶点形成三个新的三角形。3.清除超级三角形：在最后生成的三角网格中，删除所有包含超级三角形顶点的三角形。

Bowyer-Watson 算法的核心思想在于维护一个有效的 Delaunay 三角剖分，并通过检查外接圆来确保生成的三角形满足 Delaunay 条件。算法的迭代插入点过程将逐步构建出完整的三角网格。需要注意的是，Bowyer-Watson 算法并不是最高效的三角剖分算法，但它相对简单易懂，并且在许多实际应用中已经被广泛使用。
有一些更高效的算法，如 Lawson 翻转算法和S-hull 算法，可以用于生成更快速的三角剖分。

Bowyer-Watson算法 第2步 执行逻辑：

Bowyer-Watson算法 执行效果

Unity Delaunay三角剖分 应用

Unity 工程创建

随便哪个版本都行。1.新建工程2.新建一个场景（当然不新建也是可以的）3.在Hierachy 面板新建 两个Plane物体 然后放到一个你喜欢的地方4.一样在Hierachy 面板新建一个空物体并重命名为：Script5.选中Script并添加 Delaunay算法脚本（Delaunay_ZH 我的叫这个名字）
当然图省劲上面的步骤我就一一略过了  哈哈哈

点击物体  tag

Unity 预制体创建

	6.LineRender 预制体创建在 Hierachy 面板创建一个空物体并重命名为 LineRender 

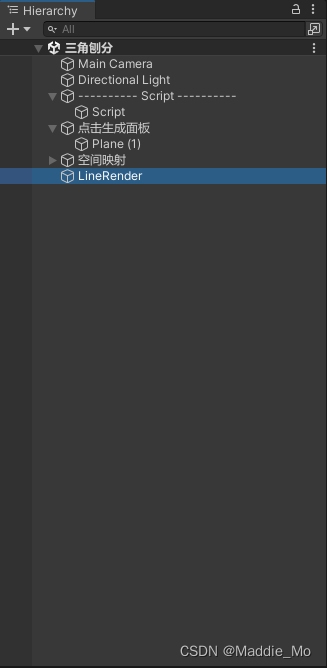
添加 LineRender 组件
当然 我这里是已经添加过了

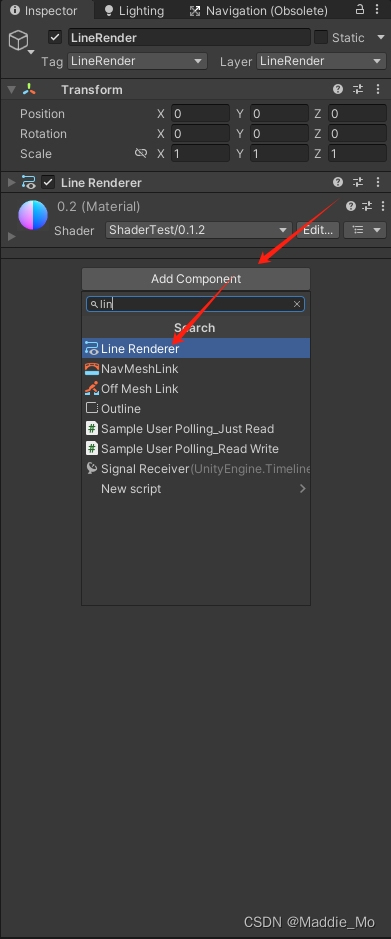
为 LineRender 组件 添加你自己喜欢的 材质球

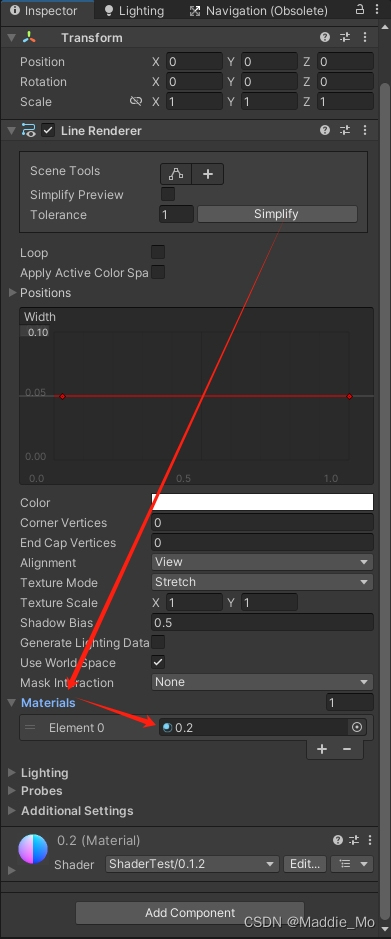
把 LineRender 物体拉到 Assets 文件夹下 生成 LineRender 预制体

	7.Mark_Prefab 预制体 创建在 Hierachy 面板创建一个空物体并重命名为 Mark_Prefab 方便后期点击生成 有限点集 V 数组  也就是顶点

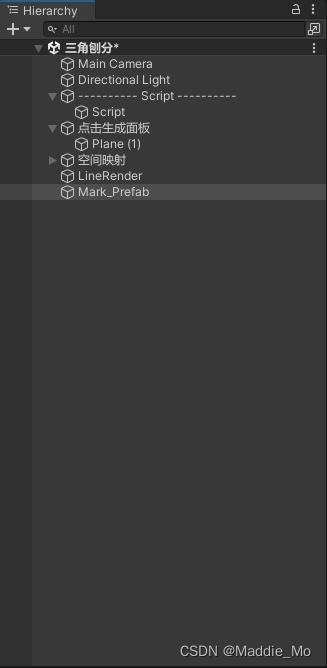
材质球赋予

把 Mark_Prefab 物体拉到 Assets 文件夹下 生成 Mark_Prefab 预制体

Unity 代码相关

Delaunay 超级三角形添加 GetTriangle

这个方法用于获取一个三角形的数组表示形式。参数含义：	参数 _a 是三角形的第一个顶点。参数 _b 是三角形的第二个顶点。参数 _c 是三角形的第三个顶点。实现逻辑：1.创建一个长度为3的 result 数组，用于存储三角形的顶点。2.将参数 _a 赋值给 result 数组的第一个元素 result[0]，表示将三角形的第一个顶点存储在数组中的第一个位置。3.将参数 _b 赋值给 result 数组的第二个元素 result[1]，表示将三角形的第二个顶点存储在数组中的第二个位置。4.将参数 _c 赋值给 result 数组的第三个元素 result[2]，表示将三角形的第三个顶点存储在数组中的第三个位置。5.返回存储了三角形顶点的 result 数组。该方法的目的是将三角形的顶点存储在一个数组中，并返回该数组。
这样可以方便地表示和传递三角形的信息。在这个特定的实现中，返回一个长度为3的数组，数组的三个元素分别为三角形的三个顶点。

  /// <summary>/// 三角形获取/// </summary>/// <param name="_a"></param>/// <param name="_b"></param>/// <param name="_c"></param>/// <returns></returns>static Vector2[] GetTriangle(Vector2 _a, Vector2 _b, Vector2 _c){Vector2[] result = new Vector2[3];result[0] = _a;result[1] = _b;result[2] = _c;return result;}

Delaunay 边界顶点存储 AddVertex

这个方法用于将新顶点添加到边界顶点存储中，更新三角形数组。参数含义：参数 _Triangles 是一个存储三角形数组的列表。参数 _NewVertex 是要添加的新顶点。实现逻辑：1.创建一个名为 _Edges 的列表，用于存储边界边的数组表示。2.使用一个循环遍历 _Triangles 列表中的每个三角形：a. 获取当前三角形的顶点数组并将其存储在变量 t0 中。b. 调用 Inside 方法判断新顶点 _NewVertex 是否在当前三角形的内部。如果是，则表示新顶点在当前三角形内部，需要进行以下操作：3.从 _Triangles 列表中移除当前三角形，使用 RemoveAt(i--)，i-- 用于保持正确的索引位置。4.将当前三角形的三条边的数组表示分别添加到 _Edges 列表中，使用 GetEdge 方法获取边的数组表示。5.使用两个嵌套循环遍历 _Edges 列表中的边界边：a. 在外层循环中，使用变量 i 遍历 _Edges 列表。b. 在内层循环中，使用变量 n 从 i+1 开始遍历 _Edges 列表。c. 获取当前边界边的数组表示并存储在变量 ei 中。d. 获取内层循环中当前边界边的数组表示并存储在变量 en 中。e. 调用 IsDoubleSide 方法判断边界边 ei 和 en 是否为双边。如果是双边，表示这两条边重叠，需要进行以下操作：6.从 _Edges 列表中移除边界边 en，使用 RemoveAt(n)。7.从 _Edges 列表中移除边界边 ei，使用 RemoveAt(i--)，i-- 用于保持正确的索引位置。8.使用 break 退出内层循环，继续下一次外层循环。9.使用 foreach 循环遍历 _Edges 列表中的边界边。a. 对于每个边界边的数组 v，调用 GetTriangle 方法将边界边的起点 v[0]、终点 v[1] 和新顶点 _NewVertex 组成一个新的三角形。b. 将新的三角形添加到 _Triangles 列表中。该方法的目的是将新顶点添加到边界顶点存储中，并根据新顶点与原有三角形的关系更新三角形数组。
它处理了新顶点在三角形内部的情况，将与新顶点相关的边界边添加到 _Edges 列表中，并根据边界边的重叠情况进行合并或移除操作，最后生成新的三角形并添加到 _Triangles 列表中。

	/// <summary>/// 边界顶点存储/// </summary>/// <param 三角形数组="_Triangles"></param>/// <param 新的顶点="_NewVertex"></param>static void AddVertex(List<Vector2[]> _Triangles, Vector2 _NewVertex){List<Vector2[]> _Edges = new List<Vector2[]>();for (int i = 0; i < _Triangles.Count; i++){//获取当前三角形Vector2[] t0 = _Triangles[i];//三角形内部判断if (Inside(t0, _NewVertex)){_Triangles.RemoveAt(i--);_Edges.Add(GetEdge(t0[0], t0[1]));_Edges.Add(GetEdge(t0[0], t0[2]));_Edges.Add(GetEdge(t0[1], t0[2]));}}for (int i = 0; i < _Edges.Count; i++){var ei = _Edges[i];for (int n = i + 1; n < _Edges.Count; n++){var en = _Edges[n];if (IsDoubleSide(ei[0], ei[1], en[0], en[1])){_Edges.RemoveAt(n);_Edges.RemoveAt(i--);break;}}}foreach (var v in _Edges){_Triangles.Add(GetTriangle(v[0], v[1], _NewVertex));}}

Delaunay 超级三角形范围判断 ContainAnyone

这个方法用于判断一个三角形是否包含在超级三角形中的任意一个顶点参数含义：参数：_Triangle 是一个由三个顶点组成的数组，表示一个三角形。参数：_Supers 是一个包含多个超级三角形的列表。每个超级三角形都由三个顶点组成，表示一个大的预设三角形。实现逻辑：1.对于给定的三角形 _Triangle 中的每个顶点 v（通过循环遍历 _Triangle 数组），执行以下步骤：2.遍历超级三角形列表 _Supers 中的每个超级三角形 sv（通过循环遍历 _Supers 列表）。3.对于超级三角形 sv 中的每个顶点 sv[m]（通过循环遍历 sv 数组），执行以下步骤：4.检查当前顶点 v 是否与超级三角形 sv 中的顶点 sv[m] 相等。如果相等，表示三角形 _Triangle 中的顶点之一与超级三角形的顶点重合，即三角形 _Triangle 包含在超级三角形中。5.如果在任何一个顶点的比较中找到了匹配，即顶点 v 与超级三角形 sv 中的顶点 sv[m] 相等，则返回 true，表示三角形 _Triangle 包含在超级三角形中的任意一个顶点。6.如果在所有的比较中都没有找到匹配，表示三角形 _Triangle 不包含在超级三角形中的任何一个顶点，返回 false。这个方法主要用于在进行三角剖分时，判断生成的三角形是否与预设的超级三角形有重叠，以便在最终结果中将这些超级三角形排除掉。

    /// <summary>/// 三角形内是否包含超级三角形中的任意一点/// </summary>/// <param 三角形="_Triangle"></param>/// <param 最大预设三角形="_Supers"></param>/// <returns></returns>static bool ContainAnyone(Vector2[] _Triangle, List<Vector2[]> _Supers){for (int i = 0; i < _Triangle.Length; i++){Vector2 v = _Triangle[i];for (int n = 0; n < _Supers.Count; n++){Vector2[] sv = _Supers[n];for (int m = 0; m < sv.Length; m++){if (v == sv[m]) return true;}}}return false;}

Delaunay 三角形 三角边获取 GetEdgeFromTriangles

这个方法用于从给定的三角形列表中获取所有的边。参数含义：参数 _Triangles 是一个包含多个三角形的列表，每个三角形由三个顶点组成。实现逻辑：1.创建一个空的 _Result 列表，用于存储所有的边。2.对于给定的三角形列表 _Triangles 中的每个三角形 t0（通过循环遍历 _Triangles 列表），执行以下步骤：3.调用 AddEdge 方法将 t0 中的第一个顶点和第二个顶点作为参数，并将结果添加到 _Result 列表中。这表示将从第一个顶点到第二个顶点的边添加到边列表中。4.调用 AddEdge 方法将 t0 中的第一个顶点和第三个顶点作为参数，并将结果添加到 _Result 列表中。这表示将从第一个顶点到第三个顶点的边添加到边列表中。5.调用 AddEdge 方法将 t0 中的第二个顶点和第三个顶点作为参数，并将结果添加到 _Result 列表中。这表示将从第二个顶点到第三个顶点的边添加到边列表中。6.循环结束后，返回存储了所有边的 _Result 列表。在三角剖分中，获取三角形的边是非常常见的操作。该方法通过遍历每个三角形，并将三角形的三条边添加到一个边列表中，最终返回了包含所有边的列表。这样可以方便进行后续的边缘处理和分析。

    /// <summary>/// 从三角形中获取边/// </summary>/// <param 预设三角形="_Triangles"></param>/// <returns></returns>static List<Vector2[]> GetEdgeFromTriangles(List<Vector2[]> _Triangles){List<Vector2[]> _Result = new List<Vector2[]>();for (int i = 0; i < _Triangles.Count; i++){var t0 = _Triangles[i];AddEdge(t0[0], t0[1], _Result);AddEdge(t0[0], t0[2], _Result);AddEdge(t0[1], t0[2], _Result);}return _Result;}

Delaunay 三角形 三角边添加 AddEdge

这个方法用于在边列表中添加一条边。参数含义：参数 _From 是边的起点。参数 _To 是边的终点。参数 _Result 是存储边的列表。实现逻辑：1.对于给定的起点 _From 和终点 _To，执行以下步骤：2.遍历边列表 _Result 中的每条边 v（通过循环遍历 _Result 列表）。3.调用 IsDoubleSide 方法，将 _From、_To 和边 v 的起点 v[0]、终点 v[1] 作为参数进行比较。4.如果 IsDoubleSide 方法返回 true，表示起点 _From 和终点 _To 与边 v 的起点和终点形成的边已经存在于边列表中，说明这条边已经被添加过了。在这种情况下，直接返回，不做任何操作。5.如果 IsDoubleSide 方法返回 false，表示起点 _From 和终点 _To 与边 v 的起点和终点形成的边不存在于边列表中，说明这条边是新的。在这种情况下，调用 GetEdge 方法，将起点 _From 和终点 _To 作为参数，获取这条边的数组表示形式，并将其添加到边列表 _Result 中。该方法的目的是避免在边列表中添加重复的边。通过遍历边列表中的每条边，并通过 IsDoubleSide 方法进行比较，如果起点和终点形成的边已经存在于边列表中，则不添加重复的边。
如果起点和终点形成的边不存在于边列表中，则将其添加到边列表中。这样可以保证边列表中的每条边都是唯一的。

    /// <summary>/// 三角边添加/// </summary>/// <param name="_From"></param>/// <param name="_To"></param>/// <param name="_Result"></param>static void AddEdge(Vector2 _From, Vector2 _To, List<Vector2[]> _Result){for (int i = 0; i < _Result.Count; i++){var v = _Result[i];if (IsDoubleSide(_From, _To, v[0], v[1])) return;}_Result.Add(GetEdge(_From, _To));}

Delaunay 三角形 双边判断 IsDoubleSide

这个方法用于判断两条边是否是双边，即两条边在相同的方向上重叠。参数含义：参数 _a0 和 _a1 是第一条边的起点和终点。参数 _b0 和 _b1 是第二条边的起点和终点。实现逻辑：1.创建两个变量 x 和 y，并初始化为 0。2.对于给定的边 _a0 和 _a1，执行以下步骤：3.将 _a0 的 x 坐标减去 _b0 的 x 坐标，并将结果累加到变量 x 中。这表示计算第一条边的起点与第二条边的起点在 x 方向上的差异。4.将 _a0 的 y 坐标减去 _b0 的 y 坐标，并将结果累加到变量 y 中。这表示计算第一条边的起点与第二条边的起点在 y 方向上的差异。5.将 _a1 的 x 坐标减去 _b1 的 x 坐标，并将结果累加到变量 x 中。这表示计算第一条边的终点与第二条边的终点在 x 方向上的差异。6.将 _a1 的 y 坐标减去 _b1 的 y 坐标，并将结果累加到变量 y 中。这表示计算第一条边的终点与第二条边的终点在 y 方向上的差异。7.判断变量 x 和 y 是否同时等于 0。如果相等，表示两条边在 x 和 y 方向上的差异都为 0，即两条边重叠在一起，可以被认为是双边。在这种情况下，返回 true。8.如果变量 x 和 y 不同时等于 0，表示两条边在 x 和 y 方向上有差异，即不重叠，不是双边。在这种情况下，返回 false。该方法通过计算两条边的起点和终点在 x 和 y 方向上的差异，判断是否为双边。如果两条边在相同的方向上重叠（差异为0），则被认为是双边。如果两条边在任何一个方向上有差异，即不重叠，则不是双边。

	/// <summary>///  是否是双边/// </summary>/// <param name="_a0"></param>/// <param name="_a1"></param>/// <param name="_b0"></param>/// <param name="_b1"></param>/// <returns></returns>static bool IsDoubleSide(Vector2 _a0, Vector2 _a1, Vector2 _b0, Vector2 _b1){float x = 0, y = 0;x += _a0.x - _b0.x;y += _a0.y - _b0.y;x += _a1.x - _b1.x;y += _a1.y - _b1.y;return x == 0 && y == 0;}

Delaunay 三角形 三角边信息添加 GetEdge

这个方法用于获取一条边的数组表示形式。参数含义：参数 _a 是边的起点。参数 _b 是边的终点。实现逻辑：1.创建一个长度为2的 result 数组，用于存储边的起点和终点。2.将参数 _a 赋值给 result 数组的第一个元素 result[0]，表示将边的起点存储在数组中的第一个位置。3.将参数 _b 赋值给 result 数组的第二个元素 result[1]，表示将边的终点存储在数组中的第二个位置。4.返回存储了边起点和终点的 result 数组。该方法的目的是将边的起点和终点存储在一个数组中，并返回该数组。这样可以方便地表示和传递边的信息。在这个特定的实现中，返回一个长度为2的数组，第一个元素是边的起点，第二个元素是边的终点。

    /// <summary>/// 三角边返回/// </summary>/// <param name="_a"></param>/// <param name="_b"></param>/// <returns></returns>static Vector2[] GetEdge(Vector2 _a, Vector2 _b){Vector2[] result = new Vector2[2];result[0] = _a;result[1] = _b;return result;}

Delaunay 三角形 外接圆判断 Inside

这个方法用于判断一个顶点是否在给定三角形的内部。参数含义：参数 _Triangle 是一个包含三角形的顶点的数组，顺序为顶点0、顶点1、顶点2。参数 _NewVertex 是要判断的新顶点。实现逻辑：1.调用 GetBisector 方法两次，分别传入 _Triangle 的顶点0和顶点1，以及 _Triangle 的顶点0和顶点2。这将返回两个垂直平分线的数组表示，分别存储在 t01 和 t02 变量中。2.调用 LineIntersection 方法，传入 t01 的起点、终点以及 t02 的起点、终点。这将计算并返回外接圆的圆心坐标，存储在 circelPoint 变量中。3.使用 Vector2.Distance 方法计算 _Triangle 的顶点0与圆心 circelPoint 的距离，得到圆心半径 r。4.使用 Vector2.Distance 方法计算新顶点 _NewVertex 与圆心 circelPoint 的距离，得到新顶点到圆心的距离 r2。5.检测 r2 是否小于等于 r，即新顶点是否在圆内。如果是，则返回 true 表示新顶点在三角形的内部；否则返回 false 表示新顶点在三角形的外部。该方法的目的是基于外接圆的概念来判断一个顶点是否在给定三角形的内部。它通过计算三角形的垂直平分线，求取外接圆的圆心，并计算圆心半径。然后，通过比较新顶点与圆心的距离，判断新顶点是否在圆内，从而确定是否在三角形的内部。

    /// <summary>/// 顶点内部判断/// 外接圆判断/// </summary>/// <param 三角形="_Triangle"></param>/// <param 顶点="_NewVertex"></param>/// <returns></returns>static bool Inside(Vector2[] _Triangle, Vector2 _NewVertex){//> 求三角形任意两边垂直平分线Vector2[] t01 = GetBisector(_Triangle[0], _Triangle[1]);Vector2[] t02 = GetBisector(_Triangle[0], _Triangle[2]);//> 求圆心Vector2 circelPoint = LineIntersection(t01[0], t01[1], t02[0], t02[1]);//> 求圆心半径float r = Vector2.Distance(_Triangle[0], circelPoint);float r2 = Vector2.Distance(_NewVertex, circelPoint);//> 检测是否在圆内 return r2 <= r;}

Delaunay 三角形 三角边相交判断 get_line_intersection

这个方法用于计算两条直线的交点。参数含义：方法的参数包括八个浮点数，分别为线段1的起点坐标 (p0_x, p0_y)、线段1的终点坐标 (p1_x, p1_y)、线段2的起点坐标 (p2_x, p2_y)、线段2的终点坐标 (p3_x, p3_y)。实现逻辑：1.声明并计算变量 s10_x 和 s10_y，分别表示线段1的横向长度和纵向长度，通过计算 p1_x - p0_x 和 p1_y - p0_y 得到。2.声明并计算变量 s32_x 和 s32_y，分别表示线段2的横向长度和纵向长度，通过计算 p3_x - p2_x 和 p3_y - p2_y 得到。3.计算变量 denom，表示两条直线的分母部分，通过计算 s10_x * s32_y - s32_x * s10_y 得到。4.声明并计算变量 s02_x 和 s02_y，分别表示线段1起点到线段2起点的横向距离和纵向距离，通过计算 p0_x - p2_x 和 p0_y - p2_y 得到。5.计算变量 t_numer，表示两条直线的分子部分，通过计算 s32_x * s02_y - s32_y * s02_x 得到。6.计算变量 t，表示两条直线的参数 t 值，通过计算 t_numer / denom 得到。7.创建一个名为 v 的 Vector2 结构变量。8.计算交点的 x 坐标，通过计算 p0_x + (t * s10_x) 得到。9.计算交点的 y 坐标，通过计算 p0_y + (t * s10_y) 得到。10.将交点的坐标存储在 v 的 x 和 y 字段中。10返回 v，即两条直线的交点坐标。该方法的目的是根据两条直线的起点和终点坐标，通过求解直线方程的参数 t 值，计算出两条直线的交点坐标。它使用了数学上的直线交点计算公式，并将结果封装在一个 Vector2 结构中返回。
作用就是求外接圆圆心  因为有了三角形任意两边垂直平分线 所以就可以使用 get_line_intersection() 直接求出当前Delaunay 三角形外接圆圆心  以及外接圆半径。

    /// <summary>/// 获得直线相交点/// </summary>/// <param name="p0_x"></param>/// <param name="p0_y"></param>/// <param name="p1_x"></param>/// <param name="p1_y"></param>/// <param name="p2_x"></param>/// <param name="p2_y"></param>/// <param name="p3_x"></param>/// <param name="p3_y"></param>/// <returns></returns>static Vector2 get_line_intersection(float p0_x, float p0_y, float p1_x, float p1_y,float p2_x, float p2_y, float p3_x, float p3_y){float s02_x, s02_y, s10_x, s10_y, s32_x, s32_y, t_numer, denom, t;s10_x = p1_x - p0_x;s10_y = p1_y - p0_y;s32_x = p3_x - p2_x;s32_y = p3_y - p2_y;denom = s10_x * s32_y - s32_x * s10_y;s02_x = p0_x - p2_x;s02_y = p0_y - p2_y;//s_numer = s10_x * s02_y - s10_y * s02_x; t_numer = s32_x * s02_y - s32_y * s02_x;t = t_numer / denom;Vector2 v;v.x = p0_x + (t * s10_x);v.y = p0_y + (t * s10_y);return v;}

Delaunay 三角形 三角边相交判断 get_line_intersection

这个方法用于获取任意线段的垂直平分线。参数含义：方法的参数 _a 和 _b 是表示线段的两个端点的二维向量。实现逻辑：1.声明并计算变量 rotate，表示旋转角度，设置为 π/2，即 90 度。2.创建一个名为 a 的向量，表示线段的方向向量，通过计算 _b - _a 得到。3.修改 _a 和 _b 的值，使得 _a 向线段方向移动一个向量 a 的距离， _b 向线段方向移动一个向量 a 的距离。这样可以确保垂直平分线的起点和终点在线段的延长线上。4.创建一个长度为2的向量数组 r，用于存储两条垂直平分线的起点和终点。5.计算垂直平分线的起点，通过以下公式计算：r[0].x = _a.x * Mathf.Cos(rotate) - _a.y * Mathf.Sin(rotate) 和 r[0].y = _a.x * Mathf.Sin(rotate) + _a.y * Mathf.Cos(rotate)。6.计算垂直平分线的终点，通过以下公式计算：r[1].x = _b.x * Mathf.Cos(rotate) - _b.y * Mathf.Sin(rotate) 和 r[1].y = _b.x * Mathf.Sin(rotate) + _b.y * Mathf.Cos(rotate)。7.计算垂直平分线的起点和终点的偏移量，通过以下公式计算：r[0].x += half.x * (1 - Mathf.Cos(rotate)) + half.y * Mathf.Sin(rotate)、r[0].y += half.y * (1 - Mathf.Cos(rotate)) - half.x * Mathf.Sin(rotate)、r[1].x += half.x * (1 - Mathf.Cos(rotate)) + half.y * Mathf.Sin(rotate)、r[1].y += half.y * (1 - Mathf.Cos(rotate)) - half.x * Mathf.Sin(rotate)。这样可以将垂直平分线的起点和终点平移到线段的中点。8.返回垂直平分线的起点和终点的数组 r。该方法的目的是通过对给定线段进行旋转和平移操作，计算出该线段的垂直平分线。它使用了数学上的旋转和平移公式，以及向量运算，来确定两条垂直平分线的起点和终点，并将结果存储在一个向量数组中返回。
作用就是为了方便计算求取Delaunay 外接圆的圆心。

    /// <summary>/// 获取任意线段的垂直平分线/// </summary>/// <param name="_a"></param>/// <param name="_b"></param>/// <returns></returns>static Vector2[] GetBisector(Vector2 _a, Vector2 _b){float rotate = Mathf.PI / 2;Vector2 a = _b - _a;_a -= a;_b += a;Vector2[] r = new Vector2[2];Vector2 half = _a + (_b - _a) / 2;r[0].x = _a.x * Mathf.Cos(rotate) - _a.y * Mathf.Sin(rotate);r[0].y = _a.x * Mathf.Sin(rotate) + _a.y * Mathf.Cos(rotate);r[1].x = _b.x * Mathf.Cos(rotate) - _b.y * Mathf.Sin(rotate);r[1].y = _b.x * Mathf.Sin(rotate) + _b.y * Mathf.Cos(rotate);r[0].x += half.x * (1 - Mathf.Cos(rotate)) + half.y * Mathf.Sin(rotate);r[0].y += half.y * (1 - Mathf.Cos(rotate)) - half.x * Mathf.Sin(rotate);r[1].x += half.x * (1 - Mathf.Cos(rotate)) + half.y * Mathf.Sin(rotate);r[1].y += half.y * (1 - Mathf.Cos(rotate)) - half.x * Mathf.Sin(rotate);return r;}

Unity Delaunay 三角剖分 代码搭载

注意预制体添加

Unity Delaunay 三角剖分 完整代码

其实整体来说难度没有那么大，可能有一两个数学相关的转换有一点点绕，不过多看两遍也就过了。
大家加油，我躺了  哈哈哈

using System.Collections;
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
using UnityEngine.Serialization;
/// <summary>
/// 三角刨分 算法
/// </summary>
public class Delaunay_ZH : MonoBehaviour
{[Header("点击位置数组")]public List<Vector2> _VecLinkedList = new List<Vector2>();[Header("目标生成")]private List<Transform> _MarkList = new List<Transform>();[Header("生成目标预制体")]public Transform _MarkPrefab;[Header("绘画 LineRender")]public LineRenderer _WaitingLr;//缓存三角形 数组public List<Vector3> _CurrentNode = new List<Vector3>();private void Awake(){Initialize();}void Update(){//鼠标点击if (Input.GetMouseButtonDown(0)){//物理射线if (Physics.Raycast(Camera.main.ScreenPointToRay(Input.mousePosition), out var _HitInfo)){//响应层if (_HitInfo.transform.gameObject.CompareTag("Target")){//点击数组 存储_VecLinkedList.Add(_HitInfo.point);//遮罩生成_MarkList.Add(Instantiate(_MarkPrefab, _HitInfo.point, Quaternion.identity));}}}if (Input.GetKeyDown(KeyCode.Q)){//绘画线条清除for (int i = 0; i < GameObject.FindGameObjectsWithTag("LineRender").Length; i++){Destroy(GameObject.FindGameObjectsWithTag("LineRender")[i]);}//剖分算法 生成 初始化var _DelaunayResult = GetTriangles2D(_VecLinkedList);//获取所有三角形数组for (int i = 0; i < _DelaunayResult.Triangles.Count; i++){//清空 初始化_CurrentNode.Clear();//获取每个三角形的顶点for (int k = 0; k < _DelaunayResult.Triangles[i].Length; k++){//_CurrentNode.Add(new Vector3(Delaunay_ZH.GetTriangles2D(_VecLinkedList).Triangles[i][k].x, Delaunay_ZH.GetTriangles2D(_VecLinkedList).Triangles[i][k].y, 0));//_CurrentNode.Add(_DelaunayResult.Triangles[i][k]);_CurrentNode.Add(new Vector3(_DelaunayResult.Triangles[i][k].x, _DelaunayResult.Triangles[i][k].y,_MarkList[0].position.z));}//绘画var _LienRender = Instantiate(_WaitingLr);GenerateVectors(_LienRender);}}if (Input.GetMouseButtonDown(2)){Initialize();}}/// <summary>/// 初始化/// </summary>public void Initialize(){//顶点数组清空_VecLinkedList.Clear();//绘画线条清除for (int i = 0; i < GameObject.FindGameObjectsWithTag("LineRender").Length; i++){Destroy(GameObject.FindGameObjectsWithTag("LineRender")[i]);}//生成物体销毁for (int t = 0; t < _MarkList.Count; t++){Destroy(_MarkList[t].gameObject);}_MarkList.Clear();}/// <summary>/// 绘画生成/// </summary>public void GenerateVectors(LineRenderer _WaitingLr){_WaitingLr.positionCount = 0;_WaitingLr.loop = true;_WaitingLr.startColor = Color.black;_WaitingLr.endColor = Color.black;_WaitingLr.startWidth = 0.05f;_WaitingLr.endWidth = 0.05f;var _PositionArray = _CurrentNode.ToArray();_WaitingLr.positionCount = _PositionArray.Length;_WaitingLr.SetPositions(_PositionArray);}/// <summary>/// Delaunay 三角剖分算法 生成/// </summary>/// <param 顶点数组="_Vertexes"></param>/// <returns></returns>public static DelaunayResult GetTriangles2D(List<Vector2> _Vertexes){//三角面数组List<Vector2[]> _Triangles = new List<Vector2[]>();//边列表List<Vector2[]> _Edges = new List<Vector2[]>();//缓存超级三角形List<Vector2[]> _Super = new List<Vector2[]>();//> 找到最小和最大的点float minX = 0, minY = 0, maxX = 0, maxY = 0, minZ = 0, maxZ = 0;//寻找最外沿顶点foreach (var v in _Vertexes){if (v.x < minX) minX = v.x;if (v.y < minY) minY = v.y;if (v.x > maxX) maxX = v.x;if (v.y > maxY) maxY = v.y;//if (v.z < minZ) minZ = v.z;//if (v.z > maxZ) maxZ = v.z;}minX -= 10;minY -= 10;minZ -= 10;maxX += 10;maxY += 10;maxZ += 10;//> 创建超级三角形Vector2 leftUp = new Vector2(minX, maxY);// 0 1 0Vector2 rightUp = new Vector2(maxX, maxY);// 1 1 0Vector2 rightDown = new Vector2(maxX, minY);// 1 0 0Vector2 leftDown = new Vector2(minX, minY);// 0 0 0//Vector3 leftUpfoward = new Vector3(minX, maxY,maxZ);// 0 1 1//Vector3 rightUpfoward = new Vector3(maxX, maxY, maxZ);// 1 1 1//Vector3 rightDownfoward = new Vector3(maxX, minY, maxZ);// 1 0 1//Vector3 leftDownfoward = new Vector3(minX, minY,  maxZ);// 0 0 1//> 为了确保所有的点都包含在三角形内//> 这里使用了两个超级三角形拼成的矩形_Super.Add(GetTriangle(leftUp, rightUp, rightDown));//(0,1,0)(1,1,0)(1,0,0)_Super.Add(GetTriangle(leftUp, rightDown, leftDown));//(0,1,0)(1,0,0)(0,0,0)//_Super.Add(GetTriangle(leftUpfoward, rightUpfoward, rightDownfoward));//(0,1,1)(1,1,1)(1,0,1)//_Super.Add(GetTriangle(leftUpfoward, rightDownfoward, leftDownfoward));//(0,1,1)(1,0,1)(0,0,1)//预设最大规则三角形_Triangles.AddRange(_Super);foreach (var v in _Vertexes)AddVertex(_Triangles, v);for (int i = 0; i < _Triangles.Count; i++){//超级三角形范围判断if (ContainAnyone(_Triangles[i], _Super)){_Triangles.RemoveAt(i--);}}var _ResultCache = new DelaunayResult();_ResultCache.Triangles = _Triangles;_ResultCache.Vertexes = _Vertexes;_ResultCache.Edges = GetEdgeFromTriangles(_Triangles);return _ResultCache;}/// <summary>/// 从三角形中获取边/// </summary>/// <param 预设三角形="_Triangles"></param>/// <returns></returns>static List<Vector2[]> GetEdgeFromTriangles(List<Vector2[]> _Triangles){List<Vector2[]> _Result = new List<Vector2[]>();for (int i = 0; i < _Triangles.Count; i++){var t0 = _Triangles[i];AddEdge(t0[0], t0[1], _Result);AddEdge(t0[0], t0[2], _Result);AddEdge(t0[1], t0[2], _Result);}return _Result;}/// <summary>/// 三角边添加/// </summary>/// <param name="_From"></param>/// <param name="_To"></param>/// <param name="_Result"></param>static void AddEdge(Vector2 _From, Vector2 _To, List<Vector2[]> _Result){for (int i = 0; i < _Result.Count; i++){var v = _Result[i];if (IsDoubleSide(_From, _To, v[0], v[1])) return;}_Result.Add(GetEdge(_From, _To));}/// <summary>/// 三角形内是否包含超级三角形中的任意一点/// 超级三角形范围判断/// </summary>/// <param 三角形="_Triangle"></param>/// <param 最大预设三角形="_Supers"></param>/// <returns></returns>static bool ContainAnyone(Vector2[] _Triangle, List<Vector2[]> _Supers){for (int i = 0; i < _Triangle.Length; i++){Vector2 v = _Triangle[i];for (int n = 0; n < _Supers.Count; n++){Vector2[] sv = _Supers[n];for (int m = 0; m < sv.Length; m++){if (v == sv[m]) return true;}}}return false;}/// <summary>/// 边界顶点存储/// </summary>/// <param 三角形数组="_Triangles"></param>/// <param 新的顶点="_NewVertex"></param>static void AddVertex(List<Vector2[]> _Triangles, Vector2 _NewVertex){List<Vector2[]> _Edges = new List<Vector2[]>();for (int i = 0; i < _Triangles.Count; i++){//获取当前三角形Vector2[] t0 = _Triangles[i];//三角形内部判断if (Inside(t0, _NewVertex)){_Triangles.RemoveAt(i--);_Edges.Add(GetEdge(t0[0], t0[1]));_Edges.Add(GetEdge(t0[0], t0[2]));_Edges.Add(GetEdge(t0[1], t0[2]));}}for (int i = 0; i < _Edges.Count; i++){var ei = _Edges[i];for (int n = i + 1; n < _Edges.Count; n++){var en = _Edges[n];if (IsDoubleSide(ei[0], ei[1], en[0], en[1])){_Edges.RemoveAt(n);_Edges.RemoveAt(i--);break;}}}foreach (var v in _Edges){_Triangles.Add(GetTriangle(v[0], v[1], _NewVertex));}}/// <summary>///  是否是双边/// </summary>/// <param name="_a0"></param>/// <param name="_a1"></param>/// <param name="_b0"></param>/// <param name="_b1"></param>/// <returns></returns>static bool IsDoubleSide(Vector2 _a0, Vector2 _a1, Vector2 _b0, Vector2 _b1){float x = 0, y = 0;x += _a0.x - _b0.x;y += _a0.y - _b0.y;x += _a1.x - _b1.x;y += _a1.y - _b1.y;return x == 0 && y == 0;}/// <summary>/// 三角边/// </summary>/// <param name="_a"></param>/// <param name="_b"></param>/// <returns></returns>static Vector2[] GetEdge(Vector2 _a, Vector2 _b){Vector2[] result = new Vector2[2];result[0] = _a;result[1] = _b;return result;}/// <summary>/// 三角形获取/// </summary>/// <param name="_a"></param>/// <param name="_b"></param>/// <param name="_c"></param>/// <returns></returns>static Vector2[] GetTriangle(Vector2 _a, Vector2 _b, Vector2 _c){Vector2[] result = new Vector2[3];result[0] = _a;result[1] = _b;result[2] = _c;return result;}/// <summary>/// 顶点内部判断/// 外接圆判断/// </summary>/// <param 三角形="_Triangle"></param>/// <param 顶点="_NewVertex"></param>/// <returns></returns>static bool Inside(Vector2[] _Triangle, Vector2 _NewVertex){//> 求三角形任意两边垂直平分线Vector2[] t01 = GetBisector(_Triangle[0], _Triangle[1]);Vector2[] t02 = GetBisector(_Triangle[0], _Triangle[2]);//> 求圆心Vector2 circelPoint = LineIntersection(t01[0], t01[1], t02[0], t02[1]);//> 求圆心半径float r = Vector2.Distance(_Triangle[0], circelPoint);float r2 = Vector2.Distance(_NewVertex, circelPoint);//> 检测是否在圆内 return r2 <= r;}/// <summary>/// 获取任意线段的交点/// </summary>/// <param name="p0"></param>/// <param name="p1"></param>/// <param name="e0"></param>/// <param name="e1"></param>/// <returns></returns>static Vector2 LineIntersection(Vector2 p0, Vector2 p1, Vector2 e0, Vector2 e1){return get_line_intersection(p0.x, p0.y, p1.x, p1.y, e0.x, e0.y, e1.x, e1.y);}/// <summary>/// 获得直线相交点/// </summary>/// <param name="p0_x"></param>/// <param name="p0_y"></param>/// <param name="p1_x"></param>/// <param name="p1_y"></param>/// <param name="p2_x"></param>/// <param name="p2_y"></param>/// <param name="p3_x"></param>/// <param name="p3_y"></param>/// <returns></returns>static Vector2 get_line_intersection(float p0_x, float p0_y, float p1_x, float p1_y,float p2_x, float p2_y, float p3_x, float p3_y){float s02_x, s02_y, s10_x, s10_y, s32_x, s32_y, t_numer, denom, t;s10_x = p1_x - p0_x;s10_y = p1_y - p0_y;s32_x = p3_x - p2_x;s32_y = p3_y - p2_y;denom = s10_x * s32_y - s32_x * s10_y;s02_x = p0_x - p2_x;s02_y = p0_y - p2_y;//s_numer = s10_x * s02_y - s10_y * s02_x; t_numer = s32_x * s02_y - s32_y * s02_x;t = t_numer / denom;Vector2 v;v.x = p0_x + (t * s10_x);v.y = p0_y + (t * s10_y);return v;}/// <summary>/// 获取任意线段的垂直平分线/// </summary>/// <param name="_a"></param>/// <param name="_b"></param>/// <returns></returns>static Vector2[] GetBisector(Vector2 _a, Vector2 _b){float rotate = Mathf.PI / 2;Vector2 a = _b - _a;_a -= a;_b += a;Vector2[] r = new Vector2[2];Vector2 half = _a + (_b - _a) / 2;r[0].x = _a.x * Mathf.Cos(rotate) - _a.y * Mathf.Sin(rotate);r[0].y = _a.x * Mathf.Sin(rotate) + _a.y * Mathf.Cos(rotate);r[1].x = _b.x * Mathf.Cos(rotate) - _b.y * Mathf.Sin(rotate);r[1].y = _b.x * Mathf.Sin(rotate) + _b.y * Mathf.Cos(rotate);r[0].x += half.x * (1 - Mathf.Cos(rotate)) + half.y * Mathf.Sin(rotate);r[0].y += half.y * (1 - Mathf.Cos(rotate)) - half.x * Mathf.Sin(rotate);r[1].x += half.x * (1 - Mathf.Cos(rotate)) + half.y * Mathf.Sin(rotate);r[1].y += half.y * (1 - Mathf.Cos(rotate)) - half.x * Mathf.Sin(rotate);return r;}}/// <summary>
/// Delaunay  结构
/// </summary>
public class DelaunayResult
{/// <summary>/// 三角形列表/// </summary>public List<Vector2[]> Triangles;/// <summary>/// 边列表/// </summary>public List<Vector2[]> Edges;/// <summary>/// 顶点列表/// </summary>public List<Vector2> Vertexes;
}

Unity Delaunay 三角剖分 运行效果

操作说明：鼠标左键：有限点集 添加鼠标中间：初始化场景键盘 Q 键：生成 Delaunay 三角网格应用领域：1.游戏开发：Delaunay 三角剖分算法在游戏开发中被广泛应用于生成地形、地图、水面、粒子效果等。通过将游戏场景中的点云数据进行三角剖分，可以方便地生成可用于碰撞检测、寻路、光照计算等的三角网格。2.动画和模拟：Delaunay 三角剖分算法可以用于生成动画或模拟中的网格变形、变形动画、粒子系统等。通过将关键点或顶点进行三角剖分，并结合插值和变形算法，可以实现各种形状的变化和动画效果。3.数据可视化：Delaunay 三角剖分算法可用于数据可视化领域，特别是在地理信息系统（GIS）和数据分析中。通过将数据点进行三角剖分并绘制三角形，可以更好地展示数据的分布、密度和关联性，帮助用户更好地理解和分析数据。4.物理模拟：Delaunay 三角剖分算法可以用于物理模拟中的碎裂效果、液体模拟等。通过将物体表面的点云数据进行三角剖分，可以生成具有真实物理特性的网格，从而实现更逼真的物理模拟效果。5.图形渲染和绘图：Delaunay 三角剖分算法可以用于生成渲染效果中的纹理映射、渐变填充、光照计算等。通过将图形或纹理上的点进行三角剖分，可以生成用于渲染和绘制的三角形网格，提供更多的绘制和渲染选项。更多的就靠大家自己发挥想象了，总之这个东西就是一个基础的算法，至于如何使用，灵活多变吧。

暂时先这样吧，如果有时间的话就会更新，实在看不明白就留言，看到我会回复的。
路漫漫其修远兮，与君共勉。