盖子的c++小课堂——第二十四讲：差分数组

前言

嗨嗨嗨，这里是盖子的小课堂哟，这次更新主要是因为快放假了，时间多了，好嘞，废话不多说，点赞评论拿来吧你~

差分数组

一维差分数组

假设给你一个数组 nums ，先对区间 [a,b] 中每个元素加 3 ，在对区间 [c,d] 每个元素减 5 …… ，这样非常频繁的区间修改，常规的做法可以一个个计算。

public void increment(int[] nums, int a, int b, int k) {for (int index = a; index <= b; index++) {nums[index] += k;}}

频繁对数组的一段区间进行增加或减去同一个值，如果一个个去操作，很明显效率很差，我们可以使用差分数组，差分数组就是原始数组相邻元素之间的差。定义差分数组 d[n] ，我们可以得到： d[i] = nums[i] − nums[i−1] ，其中 d[0] = nums[0] ，如下图所示。

我们可以看到原数组就是差分数组的前缀和。

nums[0] = d[0]num[3] = d[0] + d[1] + d[2] + d[3]

有了差分数组，如果对区间 [a,b] 每个元素加 3 ，不需要在一个个操作，只需要在两端修改即可，如下图所示。

d[a] += 3;d[b+1] -= 3;

来看下代码：

public class DiffNums {private int[] diff;// 差分数组。private int[] nums;// 原数组。public DiffNums(int[] nums) {this.nums = nums;diff = new int[nums.length];diff[0] = nums[0];for (int i = 1; i < diff.length; i++)diff[i] = nums[i] - nums[i - 1];}// 给区间[a,b]每个元素增加val（也可为负数）。public void increment(int a, int b, int val) {diff[a] += val;if (b + 1 < diff.length)diff[b + 1] -= val;}// 返回结果数组。public int[] result() {nums[0] = diff[0];for (int i = 1; i < diff.length; i++)nums[i] = diff[i] + nums[i - 1];return nums;}}

二维差分数组

我们把一维差分数组看做是一条直线，只需要用后面的值减去前面的值就可以构造差分数组。而二维差分数可以把他看做是一个平面，如下图所示，他的定义如下：

d[i][j] = a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]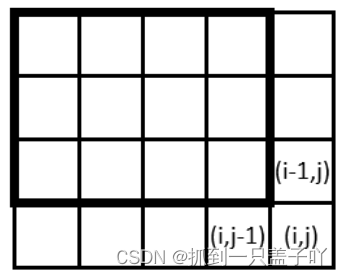

如果想获取原数组，根据上面的公式可以得到：

a[i][j] = a[i-1][j]+a[i][j-1]-a[i-1][j-1]+d[i][j]

如下图所示，以 (x1,y1) 为左上角， (x2,y2) 为右下角构成一个区间，如果对这个区间内的每个元素增加 val ，只需要执行下面四步即可。

public void add(int x1, int y1, int x2, int y2, int val) {d[x1][y1] += val;// 增加S1d[x1][y2 + 1] -= val;// 减去S2d[x2 + 1][y1] -= val;// 减去S3d[x2 + 1][y2 + 1] += val;//加上S4}

代码如下：

private int[][] d;// 差分数组。private int[][] a;// 原数组。public TwoDiffNums(int[][] a) {this.a = a;int m = a.length;int n = a[0].length;d = new int[m][n];// 求差分数组。for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)add(i, j, i, j, a[i][j]);}public void add(int x1, int y1, int x2, int y2, int val) {d[x1][y1] += val;if (y2 + 1 < d[0].length)d[x1][y2 + 1] -= val;if (x2 + 1 < d.length)d[x2 + 1][y1] -= val;if (x2 + 1 < d.length && y2 + 1 < d[0].length)d[x2 + 1][y2 + 1] += val;}// 返回结果数组。public int[][] result() {for (int i = 0; i < a.length; i++) {for (int j = 0; j < a[0].length; j++) {int x1 = i > 0 ? a[i - 1][j] : 0;int x2 = j > 0 ? a[i][j - 1] : 0;int x3 = i > 0 && j > 0 ? a[i - 1][j - 1] : 0;a[i][j] = x1 + x2 - x3 + d[i][j];}}return a;}

差分数组是与前缀和数组所对应的一种逆操作，类似于求导和积分，也就是说，对差分数组求前缀和，可以得到原数组，同样的，对前缀和数组求差分，也可以得到原数组。