
一、说明
二、SymPy — 函数类
SymPy 包包含 sympy.core.function 模块中的 Function 类。该类作为各种数学函数的基础,也充当未定义函数类的构造函数。
以下类别的函数继承自 Function 类 -
- 复数函数
- 三角函数
- 整数函数
- 组合函数
- 其他杂项功能
三、复数函数
这组函数在sympy.functions.elementary.complexes模块中定义。
-
re -- 该函数返回表达式的实部
from sympy import *
re(5+3*I)Output:
5re(I)Output:
0-
Im --表达式的虚部
im(5+3*I)Output:
3im(I)Output:
1-
sign --表达式的符号
他的函数返回表达式的复数符号。
对于真实的表达,符号将是 -
- 1 如果表达式为正
- 如果表达式等于 0,则为 0
- 如果表达式为负数,则为 -1
如果表达式是虚数,则返回的符号为 -
- I 如果 im(表达式) 为正
- -I 如果 im(表达式) 为负数
sign(1.55), sign(-1), sign(S.Zero)Output:
(1, -1, 0)sign (-3*I), sign(I*2)Output:
(-I, I)-
Abs
该函数计算复数的大小,测量复平面上从原点 (0,0) 到点 (a, b) 的距离。它是 abs() 函数的扩展,允许符号输入。
Abs(2+3*I)Output:
√13-
conjugate -- 共轭
该函数返回复数的共轭。为了找到复共轭,我们改变虚部的符号。
conjugate(4+7*I)Output:
4 - 7i四、三角函数(Trigonometric functions)
SymPy 提供三角函数的定义,如正弦、余弦、正切及其反函数(asin、acos、atan),以计算以弧度表示的角度值。
sin(pi/2), cos(pi/4), tan(pi/6)Output:
(1, sqrt(2)/2, sqrt(3)/3)asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)Output:
(pi/2, pi/4, pi/6)五、整数函数
这是一组函数,旨在对整数执行各种操作。
- 天花板Ceiling
这是一个单变量函数,提供大于或等于其输入的最小整数值。处理复数时,向上运算分别应用于实部和虚部。
ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)Output:
(4, 7, 3 + 4*I)地面floor
此函数提供小于或等于输入参数的最大整数的整数值。处理复数时,此函数独立确定实部和虚部的下限值。
floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)Output:
(3, 16, 6 - 6*I)压裂frac
该函数表示 x 的小数部分。
frac(3.99), frac(Rational(10,3)), frac(10)Output:
(0.990000000000000, 1/3, 0)六、组合函数
组合学处理与有限或离散系统中的选择、排列和操作元素相关的数学问题。
阶乘
阶乘在组合数学中起着至关重要的作用,它决定了 n 个对象的排列。记为𝑥!并用作非负整数阶乘的实现。对于负整数,阶乘结果为复无穷大。
x=Symbol('x')
factorial(x)Output:
x!factorial(5)Output:
120factorial(-1)Output:
∞∽七、二项式binomial
该函数表示我们可以从 n 个元素的集合中选择 k 个元素的方式数。
x,y=symbols('x y')
binomial(x,y)Output:
(x/y)binomial(4,2)Output:
6Rows of Pascal's triangle can be generated with the binomial function.for i in range(5): print ([binomial(i,j) for j in range(i+1)])Output:
[1][ 1, 1 ] [1, 2, 1][1, 3, 3, 1][1, 4, 6, 4, 1]斐波那契
斐波那契数列以 F0=0 和 F1=1 开始,后续的每一项都通过添加前面的两项来确定 (Fn=Fn−1+Fn−2)。
[fibonacci(x) for x in range(10)]Output:
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]tribonacci
Tribonacci 数形成一个整数序列,从 F0=0、F1=1、F2=1 开始,后续的每一项都是前面三项的和 (Fn=Fn-1+Fn-2+Fn-3) 。
tribonacci(5, Symbol('x'))Output:
x^8+3x^5+3x^2[tribonacci(x) for x in range(10)]Output:
[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]八、杂项功能
以下是一些常用功能的汇总:
- Min:此函数提供列表中的最小值。它被命名为“Min”是为了防止与内置函数“min”发生冲突。
- Max:当您需要列表中的最大值时,“Max”函数可以满足您的需求,旨在避免与内置“max”函数发生冲突。
- root:“root”函数用于获取给定数字 x 的 n 次方根。
- sqrt:如果您对数字的主平方根感兴趣,可以使用“sqrt”函数。
- cbrt:“cbrt”函数计算数字的主立方根,这是 x++Rational(1,3) 的便捷快捷方式。
现在,让我们看一些示例,说明这些杂项函数的用法及其相应的结果。
Min(pi,E)Output:
eMax(5, Rational(11,2))Output:
11/2root(7,Rational(1,2))Output:
49sqrt(2)Output:
√2cbrt(1000)Output:
10九、SymPy — 四元数
在数学领域,四元数系统是比复数更广泛的框架。在每个四元数实体中,存在四个标量变量,包含一个真实维度和三个虚构维度。
四元数由以下表达式表示:
q = a + bi + cj + dk
在此表达式中,“a”、“b”、“c”和“d”都是实数值,而“i”、“j”和“k”表示四元数单位。值得注意的是,这些单位满足以下关系:i² = j² = k² = ijk。
四元数类可以在 sympy.algebras.quaternion 模块中找到。
from sympy.algebras.quaternion import Quaternion
q=Quaternion(2,3,1,4)
qOutput:
2+3i+1j+4k四元数用于纯数学,也用于应用数学、计算机图形学、计算机视觉等。
from sympy import *
x=Symbol('x')
q1=Quaternion(x**2, x**3, x)
q1Output:
x^2+x^3i+xj+0k四元数对象也可以有虚数系数
q2=Quaternion(2,(3+2*I), x**2, 3.5*I)
q2Output:
2+(3+2i)i+x2j+3.5ik十、添加 add()
Quaternion 类中提供的此方法执行两个 Quaternion 对象的加法。
q1=Quaternion(1,2,3,4)
q2=Quaternion(4,3,2,1)
q1.add(q2)Output:
5+5i+5j+5k可以在四元数对象中添加数字或符号。
q1+2Output:
3+2i+3j+4kq1+xOutput:
(x+1)+2i+3j+4k十一、乘法mul()
此方法执行两个四元数对象的乘法。
q1=Quaternion(1,2,1,2)
q2=Quaternion(2,4,3,1)
q1.mul(q2)Output:
(−11)+3i+11j+7k十二、逆inverse()
此方法返回四元数对象的逆。
q1.inverse()Output:
1/10+(−1/5)i+(−1/10)j+(−1/5)k十三、pow()
此方法返回四元数对象的幂。
q1.pow(2)Output:
(−8)+4i+2j+4k十四、指数exp()
此方法计算四元数对象的指数,即 eq
q=Quaternion(1,2,4,3)
q.exp()
十五、SymPy — 求解器 Solvers
由于Python的符号=和==作为赋值运算符和相等运算符具有特定含义,因此它们不适合表达符号方程。为了创建符号方程,SymPy 提供了 Eq() 函数作为专用工具。
from sympy import *
x,y=symbols('x y')
Eq(x,y)Output:
x = ySince x=y is possible if and only if x-y=0, above equation can be written as −Eq(x-y,0)Output:
x − y = 0SymPy 中的求解器模块提供了 soveset() 函数,其原型如下 -
solveset(equation, variable, domain)默认情况下,域为 S.Complexes。使用solvet()函数,我们可以求解代数方程如下 -
solveset(Eq(x**2-9,0), x)Output:
{−3, 3}solveset(Eq(x**2-3*x, -2),x)Output:
{1,2}Solveset 的输出是解的有限集。如果没有解决方案,则返回 EmptySet
solveset(exp(x),x)Output:
∅十六、线性方程
我们必须使用 linsolve() 函数来求解线性方程。
例如,方程如下 -
xy=4
x+y=1
from sympy import *
x,y=symbols('x y')
linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))Output:
{(5/2,−3/2)}linsolve() 函数还可以求解以矩阵形式表示的线性方程。
a,b=symbols('a b')
a=Matrix([[1,-1],[1,1]])
b=Matrix([4,1])
linsolve([a,b], (x,y))Output:
{(5/2,−3/2)}十六、非线性方程
为此,我们使用 nonlinsolve() 函数。这个例子的方程 -
a2+a=0 ab=0
a,b=symbols('a b')
nonlinsolve([a**2 + a, a - b], [a, b])Output:
{(−1,−1),(0,0)}十七、微分方程
首先,通过将 cls=Function 传递给符号函数来创建一个未定义的函数。要求解微分方程,请使用 dsolve。
x=Symbol('x')
f=symbols('f', cls=Function)
f(x)Output:
f(x)Here f(x) is an unevaluated function. Its derivative is as follows −f(x).diff(x)Output:
d/dxf(x)We first create Eq object corresponding to following differential equationeqn=Eq(f(x).diff(x)-f(x), sin(x))
eqnOutput:
−f(x)+d/dxf(x)=sin(x)dsolve(eqn, f(x))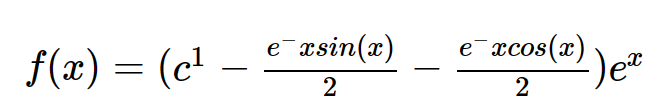
所以就是这样。这些函数是重要的构建块,构成模拟复杂数学情况的重要组成部分。




)








HDFS源码剖析)
)




