文章目录
- 回溯法
- 迷宫游戏
- N皇后问题
- 基本概念
- 解空间
- 4后问题的解空间
- 可行解和最优解
- 回溯法
- 回溯法术语
- 回溯法的关键问题
- 回溯法的基本思想
- 4后问题的约束条件
- n后问题
- 生成问题状态的基本方法
- ==子集和问题==
- 一个朴素的求解方法
- 回溯
- 回溯法的剪枝技术
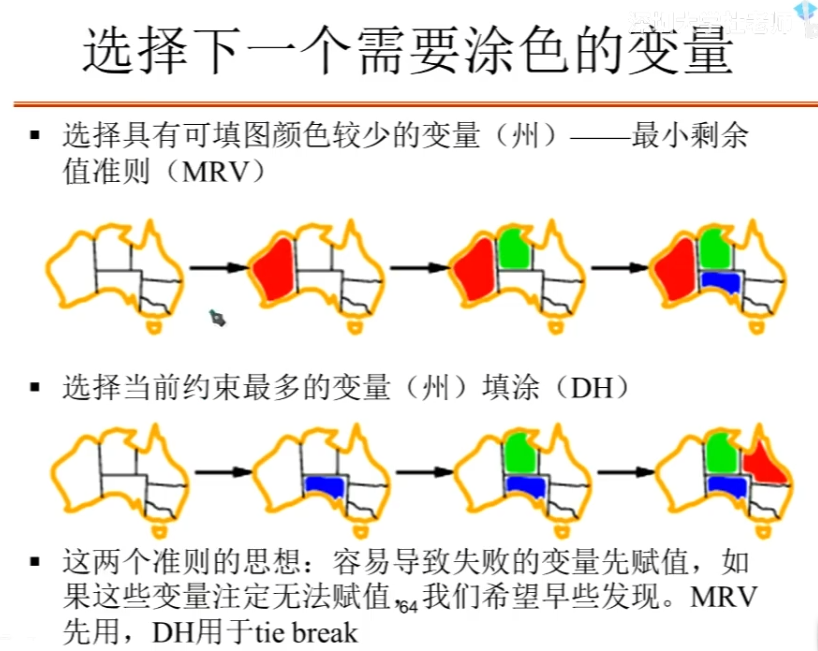
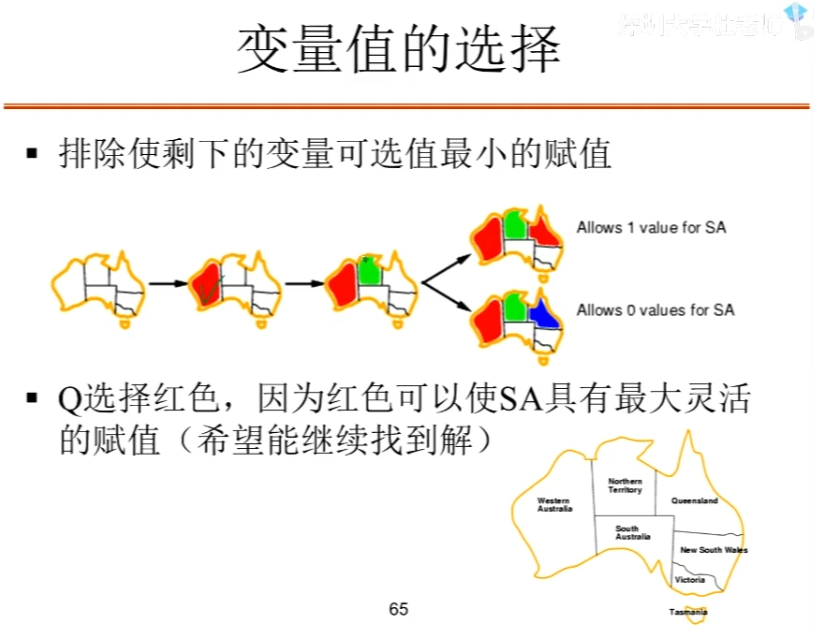
- 地图填色问题
回溯法
迷宫游戏
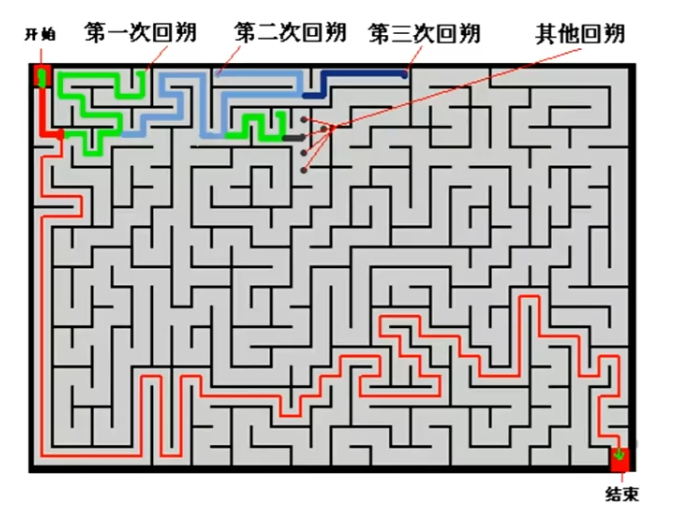
深度优先遍历。某一条线路卡死了就回溯回来。
这种回溯思想,和一个完全蛮力的蛮力法相比,它的好处:
1)不用遍历所有的路线;
2)不用每次都从起点开始。
它只是回溯到分叉点的地方,再去选另一条路走,而不是每次都从迷宫起点开始。
不过说白了,回溯法其实就是蛮力法的一种,说白了回溯法也就是个蛮力法。
-
主要思想
- 用于发现所有或者部分解的一种通用策略
- 逐步构建部分备选解(partial candidates to the solutions)
- 如果备选解不能成为一个有效的解,则立即放弃该分支
-
求可行解问题
- 八皇后问题
- 子集和问题
-
求最优解问题
- 0/1背包问题
-
回溯法只能用于问题可以分解为部分备选解(partial candidate solutions),并可以快速检验部分备选解是否能够成为一个有效的解。
-
如果可行,回溯法一般比蛮力法要快得多,因为回溯法可以排除一群备选解。
N皇后问题
皇后指的就是国际象棋里面那个叫皇后的棋子。
- 在n×n格的棋盘上放置彼此不受攻击的n个皇后。按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
- n后问题等价于在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
- n=1显而易见。n=2、3,问题无解。n>=4时,问题才有意义。
以4后为例
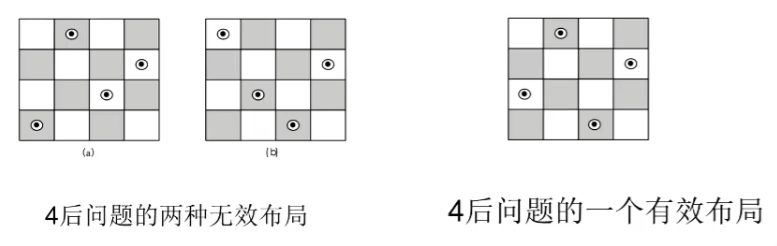
蛮力法
把所有的情况全部列出来。
比如,第一个皇后放在第一行第一列,那么第二个皇后能够放在哪些位置、第三个皇后继而能够放在哪些位置、第四个皇后继而能够放在哪些位置。
第一个皇后放在第一行第二列时,第二、三、四个……放在什么位置。
感觉没说太清楚,但是就是这个意思,通过蛮力法求出所有可能的摆放情况。
总之,可见,n比较小的时候,也许蛮力法还可以,比如七八个皇后,蛮力法勉强也行。但是数量大了以后,就很困难了。
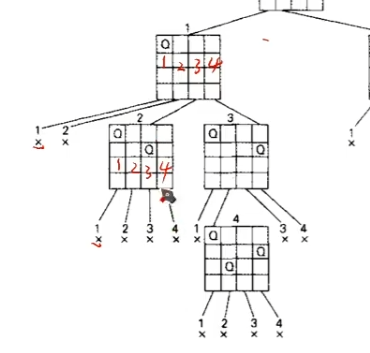
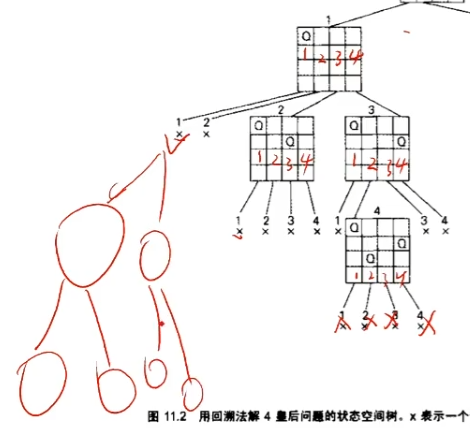
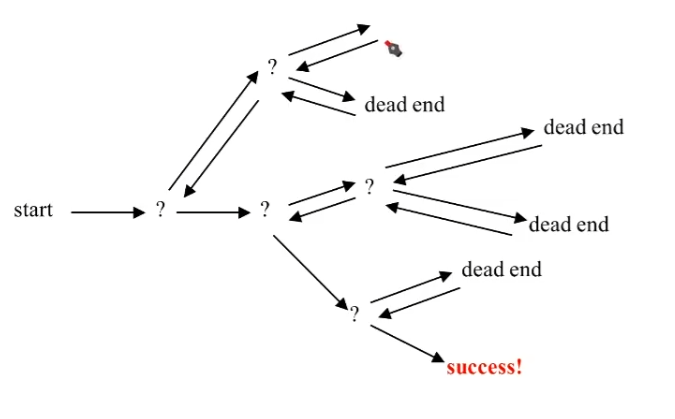
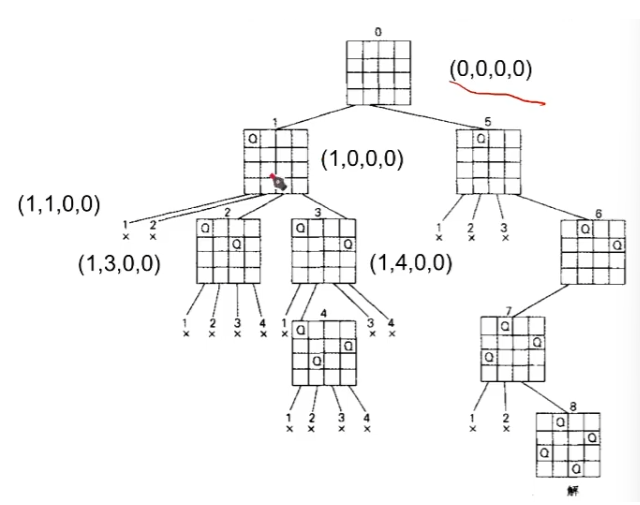
4皇后问题,采用回溯法,求解过程图示
采用深度优先遍历(DFS)。
(你如果要说BFS行不行,也没啥问题,只不过是另一种方式了)
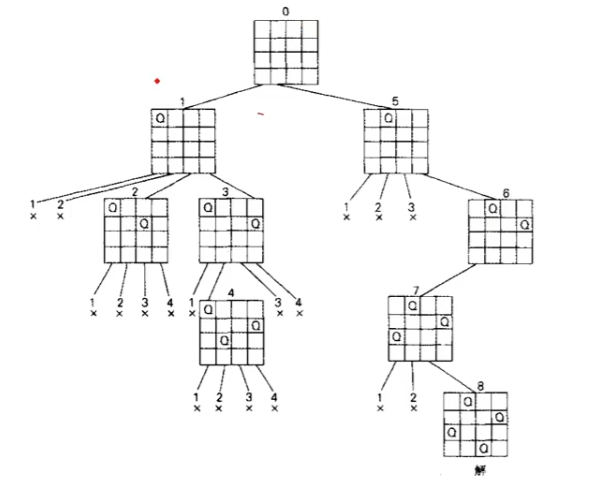
啥意思呢,比如:
第一行,在第一列摆一个皇后。
那么第二行的那个皇后,总共有4种摆法,分别为1、2、3、4。
第二行摆在1——不可行,回退。
第二行摆在2——不可行,回退。
第二行摆在3——可行,进一步讨论:
——第三行摆在1,不可行,回退;
——第三行摆在2,不可行,回退;
——第三行摆在3,不可行,回退;
——第三行摆在4,不可行,回退;
第二行摆在4——可行,进一步讨论:
——第三行摆在1,不可行,回退;
——第三行摆在2,可行,进一步讨论:
————第四行摆在1,不可行,回退;
————第四行摆在2,不可行,回退;
————第四行摆在3,不可行,回退;
————第四行摆在4,不可行,回退。
——第三行摆在3,不可行,回退;
——第三行摆在4,不可行,回退;
至此,对于第一行摆在第一位的所有“进一步讨论”的结果,均无法得到最终可行方案,均回退。
所以,之后又该讨论“第二行摆在位置2”下面所有的可能情况,同理,可行的就进一步讨论,不可行的就排除并回退。
这个问题和走迷宫本质是同样的,走不通就回退并排除,最终找到一个可行的解。
可见,它其实也是在蛮力。只不过它和蛮力还是有区别的:
什么是蛮力法?就是,我即使这个方法已经不可行了,但是我还是要把它下面所有的分支遍历一遍并且讨论一下。
回溯法是,当我这里不可行了,它下面的是什么东西我根本就不去看它了。
所以,回溯法其实就是一种蛮力法,而不是什么高级的办法。只不过是说,回溯法,当我发现这个情况不可行了,那我在它后续的所有结点就不需要去找了。
回溯法就是一种“剪枝”的蛮力法。而纯粹的蛮力法是不剪枝的。
思路大致明白了,再思考一些问题
问题
1、解怎么表示?
2、解如何组织?
3、怎么找到最优解?
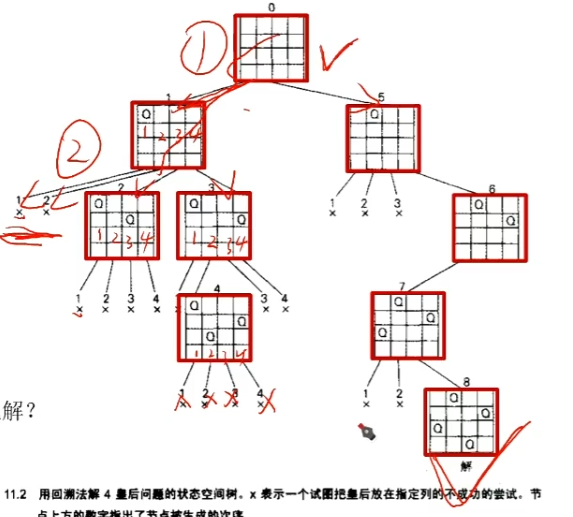
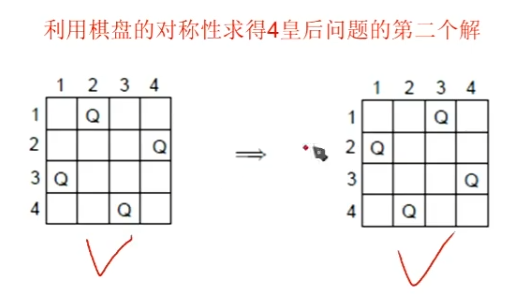
除了找到的这1个解,还有没有其他解?——肯定有。因为“对称”的情况,和它是一样的,肯定也是它的解。
而我只搜索到一个解就结束了。后面不管还有没有其他的解,都不看了。
如果找到一个可行解之后,还想找其他的解。
继续使用回溯法查找,就可以得到问题的其他解。
n皇后问题——n-Queens Problem
- 在做4皇后问题时,有没有什么办法可以优化一下问题搜索呢?
刚才也说了,找到一个可行解之后,我们最起码可以用“对称性”再找另外几个解出来。
基本概念
- 解空间
- 可能解
- 可行解
- 最优解
解空间
- 问题的解向量 X = ( x 0 , x 1 , . . . , x n − 1 ) X=(x_0,x_1,...,x_{n-1}) X=(x0,x1,...,xn−1)——解的表达形式。
- x i x_i xi的取值范围 S i S_i Si, S i = { a i . 0 , a i . 1 , . . . , a i , m i } S_i=\{a_{i.0},a_{i.1},...,a_{i,m_i}\} Si={ai.0,ai.1,...,ai,mi}。
- 问题的解空间由笛卡尔积 A = S 0 × S 1 × . . . × S n − 1 A=S_0×S_1×...×S_{n-1} A=S0×S1×...×Sn−1构成。
4后问题的解空间
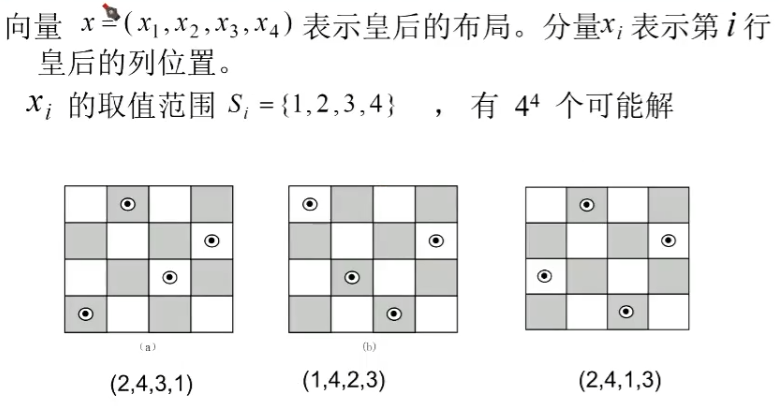
例如:4皇后问题:
解向量 x = ( x 1 , x 2 , x 3 , x 4 ) x=(x_1,x_2,x_3,x_4) x=(x1,x2,x3,x4):4维的向量。
x i x_i xi表示第 i i i行皇后的列位置,取值范围 S i = { 1 , 2 , 3 , 4 } S_i=\{1,2,3,4\} Si={1,2,3,4}。
解空间——4维向量的全部组合。
可行解和最优解
- 可行解:满足约束条件的解,解空间中的一个子集。
区分“可能解”与“可行解”。
- 最优解:使目标函数取极值(极大或极小)的可行解,一个或少数几个。
达到“最优”时的可行解。可能有1个,也可能有少数的几个。
- 找可行解,一般找到就可以,但是找最优解一般要遍历整棵树。
打个比方,比如,一个男的要找个女朋友。
解空间:所有女的。(男的就不在我解空间里面了)
可能解:所有女的里面,哪些跟我是有可能成功的。(比如那些已婚的就不是可能解)
可行解:有一些条件,比如年龄之类的?——满足约束条件的解。(虽然可能,但是得符合我规定的一些条件)
最优解:能够让一些条件达到极值,此时就是最优解。
实际上,由此可见,在“可行解”和“最优解”之间还会有一种“满意解”。
最优解可能不是那么好找,但是光是可行解还感觉不够,可以找一个满意解,尽量能贴近最优解,我就比较满足了。
回溯法
有“通用解题法”之称,将所有的解(问题的解空间)按照一定结构排列,再进行搜索。
- 一般解空间构造成树状结构,用深度优先的策略搜索。
- 两种方式:
- 只需要一个解的话,找到解就停止。
- 需要求所有解,则需做“树的遍历”找到所有解。
- 通常用排除法(剪枝),减少搜索空间。
如果不考虑最后一条,不剪枝,它就是纯蛮力法了。
-
给定问题有一个约束集合以及目标函数。
-
可以用状态空间树
state space tree来表示解空间。- 状态空间树的根代表了
0个选择的状态。 - 深度为
1的节点代表第1次选择后的状态。 - 深度为
2的节点代表第2次选择后的状态。 - ……
- 状态空间树上一条从根到叶子的路径代表了备选解。
- 状态空间树的根代表了
-
可行问题(Feasibility problem):一些选择可以到达可行的解,一些选择不能达到可行解。
回溯法术语
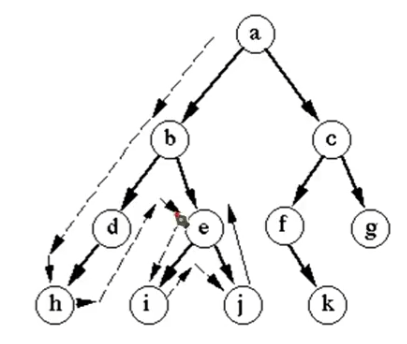
树由节点组成:
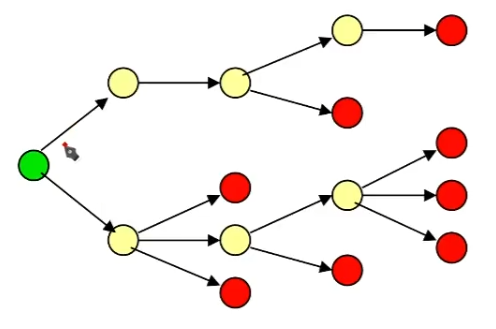
有三种节点:
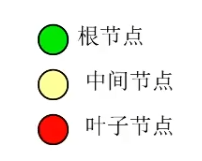
回溯法就是搜索树中某个特定目标节点。
一些特征
- 树中每个非叶子结点都是一个或是多个其他结点的父结点。
- 树中结点(除了根结点)都只有一个父结点。
回溯法的关键问题
- 结点的含义是什么?(根据问题确定)
- 结点在树中的关系是什么?(根据问题确定)
- 如何产生新的结点?(树的遍历算法)
- 如何判断结点是否是所求解?
这四点实际上不仅仅是回溯法的关键,它其实也是蛮力法的关键。
当然,回溯法实际上还有个第五点:剪枝。
回溯法的基本思想
- 针对所给问题,定义问题的解空间。(定义结点)
- 确定易于搜索的解空间结构。(定义结点关系)
- 以深度优先方式搜索解空间(产生新结点),并在搜索过程中用剪枝函数避免无效搜索(尽量少产生新结点)。
常用剪枝函数:用约束函数在扩展结点处剪去不满足约束的子树。
4后问题的约束条件
-
4后问题状态空间树:4叉完全树
-
约束方程: 1 ≤ i ≤ 4 , 1 ≤ j ≤ 4 , i ≠ j 1≤i≤4,1≤j≤4,i≠j 1≤i≤4,1≤j≤4,i=j
-
不在同一列:第
i行皇后列位置与第j行皇后列位置不同,即 x i ≠ x j x_i≠x_j xi=xj。 -
不在同一个斜线上: ∣ x i − x j ∣ ≠ ∣ i − j ∣ |x_i-x_j|≠|i-j| ∣xi−xj∣=∣i−j∣。
则求解过程:
- 向量 x = ( x 1 , x 2 , x 3 , x 4 ) x=(x_1,x_2,x_3,x_4) x=(x1,x2,x3,x4)表示皇后的布局。分量 x i x_i xi表示第
i行皇后的列位置。 - x i x_i xi的取值范围 S i = { 1 , 2 , 3 , 4 } S_i=\{1,2,3,4\} Si={1,2,3,4}
n后问题
- 解向量: ( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn)
- 显约束: x i = 1 , 2 , . . . , n x_i=1,2,...,n xi=1,2,...,n
- 隐约束:
- 不同列: x i ≠ x j x_i≠x_j xi=xj
- 不处于同一正、反对角线: ∣ i − j ∣ ≠ ∣ x i − x j ∣ |i-j|≠|x_i-x_j| ∣i−j∣=∣xi−xj∣
bool Queen::Place(int k) { //检查前k行是否合法for(int j=1; j<k; j++) {if( abs(k-j)==abs(x[j]-x[k]) || (x[j]==x[k]) )return false;}return true;
}void Queen::Backtrack(int t) { //对第t行放置皇后if(t>n) //当层数大于n时,说明前n行都放好了。可行解的个数+1sum++;else {for(int i=1; i<=n; i++) {x[t] = i;if(Place(t))Backtrack(t+1); //如果可以放置,继续找下一行位置}}
}
这样一个递归地遍历的过程,实际上就是一个深度优先的遍历。
生成问题状态的基本方法
- 扩展结点:一个正在产生儿子的结点称为扩展结点。
- 活结点:一个自身已生成但其儿子还没有全部生成的结点称作活结点。
- 死结点:一个所有儿子已经产生的结点称作死结点。
- 深度优先的问题状态生成法:如果对一个扩展结点R,一旦产生了它的一个儿子C,就把C当做新的扩展结点。在完成对子树C(以C为根的子树)的穷尽搜索之后,将R重新变成扩展结点,继续生成R的下一个儿子(如果存在)。
- 宽度优先的问题状态生成法:在一个扩展结点变成死结点之前,它一直是扩展结点。
- 回溯法:为了避免生成那些不可能产生最佳解的问题状态,要不断地利用限界函数(bounding function)来处死那些实际上不可能产生所需解的活结点,以减少问题的计算量。具有限界函数的深度优先生成法称为回溯法。
子集和问题
- 问题:给定n个正整数 w 1 , . . . w n w_1,...w_n w1,...wn集合,一个正整数 S S S,找到所有子集,使其和等于 S S S。
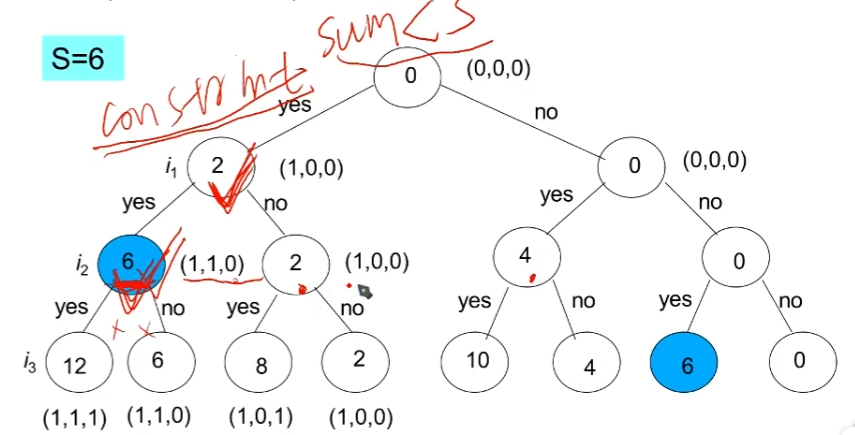
举例: n = 3 , w 1 = 2 , w 2 = 4 , w 3 = 6 , S = 6 n=3,w_1=2,w_2=4,w_3=6,S=6 n=3,w1=2,w2=4,w3=6,S=6.
解: { 2 , 4 } a n d { 6 } \{2,4\}and\{6\} {2,4}and{6}
蛮力法:找出集合所有的子集合。——时间复杂度 O ( 2 n ) O(2^n) O(2n),因此问题规模很大时不适用。
- 为了更好解决问题,利用回溯法。
- 向量 x = ( x 1 , x 2 , . . . , x n ) x=(x_1,x_2,...,x_n) x=(x1,x2,...,xn)表示节点,每个 x i x_i xi的取值范围 { 0 , 1 } \{0,1\} {0,1}。
- 使用二叉状态空间树binary state space tree进行回溯
- 深度为0的根结点:表示0个元素的集合的和
- 深度为1的结点是包括元素1或者不包括元素1
- 对每个深度为 i − 1 i-1 i−1的结点,左分支包括 w i ( ′ y e s ′ ) w_i('yes') wi(′yes′),右分支包括 w i ( ′ n o ′ ) w_i('no') wi(′no′)。
- 每个结点赋予一个值,表示当前求和大小。
但是至此,这说的还是纯粹的穷举法啊。
一个朴素的求解方法
-
构造二叉状态空间树
-
检查每个叶子结点,该结点的值是否是 S S S,如果是,返回从根到叶子结点的路径。
- 检查可以在构造树的时候进行,也可以在树构造好之后进行。
- 问:既然可以在构造树的时候进行,那为什么还要在树构造好之后进行?
- 答:也许我们想求得对于 S S S不同的子集。
- 检查可以在构造树的时候进行,也可以在树构造好之后进行。
-
要找到所有的解,我们要用一种方法来系统地遍历整个树。
注意:叶子结点之间没有指针相连。
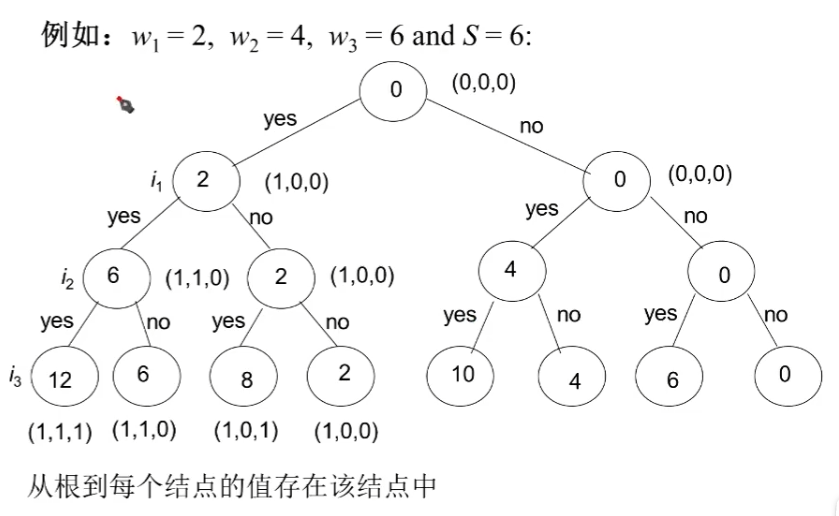
我们先对这些正整数做一个排序,这样对我们之后的工作有好处。
把整个树已经构建出来了,这个就是我们的状态空间树。
接下来,我们对这棵树做深度优先搜索。
深度优先搜索
- 使用深度优先搜索(Depth First Search,DFS)以找到所有的正确的解。
- DFS:
- 开始从根搜索。
- 搜索从最近访问的结点v到下一个新的结点
- 如果该结点的左子结点还没有被访问,访问该左子结点
- 否则,如果该结点的右子结点还没有被访问,访问该右子结点
- 否则,如果v是叶子结点,或者v的所有子树都已经被访问,返回v的父结点
- 直到所有结点都被访问。
深度优先搜索的算法此处就不展开讲了,应该是会的。
DFS(v)if v = NILreturnexplore(v)DFS(left(v))DFS(right(v))
初始调用: D F S ( T . r o o t ) DFS(T.root) DFS(T.root)。
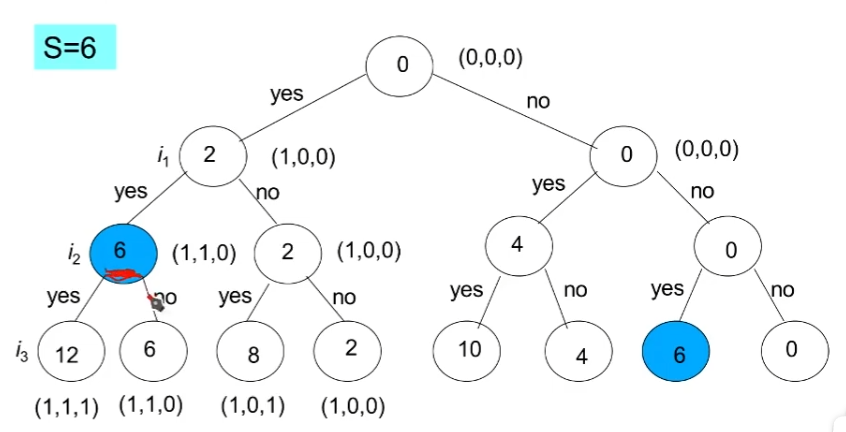
那好,我对这棵树做深度优先搜索,我找到为6的结点了,那这个结点再往下的任何子结点我都不需要再去看了。
然后继续深度优先遍历其余的地方,一直找找找……。后面的遍历过程中可能又找到了一个为6的结点。
**注意:**这里就体现刚才所说的,检查每个叶子结点,该结点的值是否是 S S S,如果是,返回从根到叶子结点的路径。**检查可以在构造树的时候进行,也可以在树构造好之后进行。**这个道理了。
如果你是在构建树的过程中检查,就会导致:我构建的过程中构建了一个
6出来,我就结束了,其他的我全都不管了。而如果我是在构造完毕整个树之后,才去做深度优先进行检查,就能找到所有的情况了。
- 用DFS找到子集和问题的所有解
- 在DFS中,检查结点v是否是叶子结点
- 如果是叶子结点,检查当前和是否是S
- 问题:非常慢
- 有n个输入项的树,有 2 n 2^n 2n叶子结点。
比如上面那个例子,
我每次判断
sum < S,若符合,则继续向下面去深度遍历,否则就不必继续。但即使这样,我仍旧会有大量的路要走,所花费的代价还是很高。
这个时候,我们就运用我们的回溯法,加速它。
回溯
-
用回溯法加速DFS算法,以避免访问没有希望的结点。
-
如果该结点不能产生一个可行解,那么该结点是没有希望的
non-promising。否则该结点就是有希望的promising。 -
主要思路:
- 在状态空间树上做深度优先搜索
- 检查该结点是否是有希望的
- 如果该结点是没有希望的,返回其父结点
-
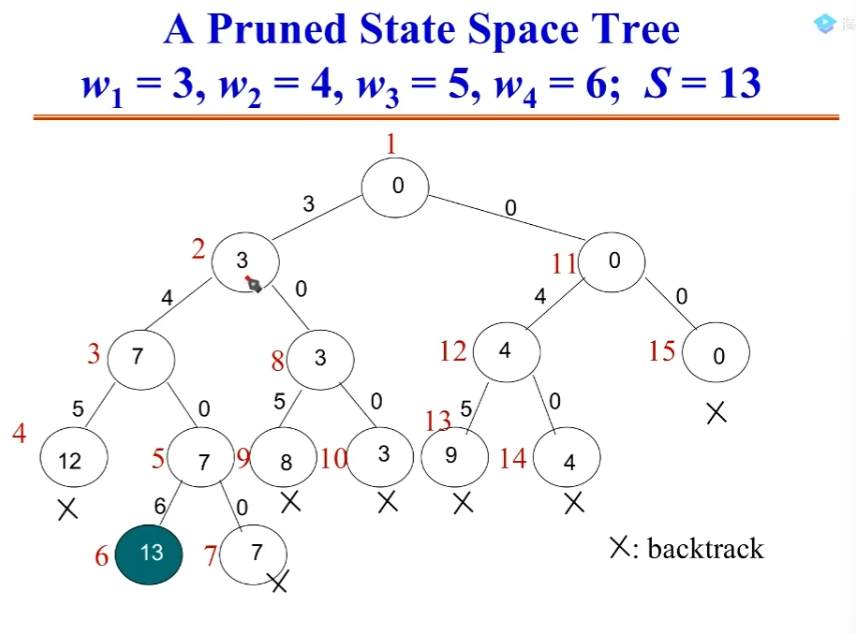
包含被访问结点的子树被称为被剪枝状态空间树
pruned state space tree。
回溯法的剪枝技术
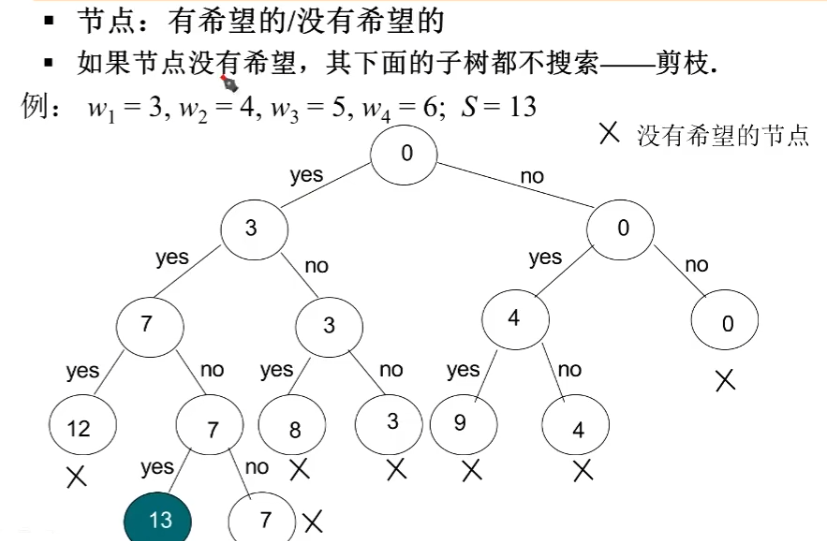
因为我们可供选择的数字是经过递增排序过了的。
所以对于第四层的
12来说,它再往下不可能加出13来,它就是没有希望的。其他结点同理。
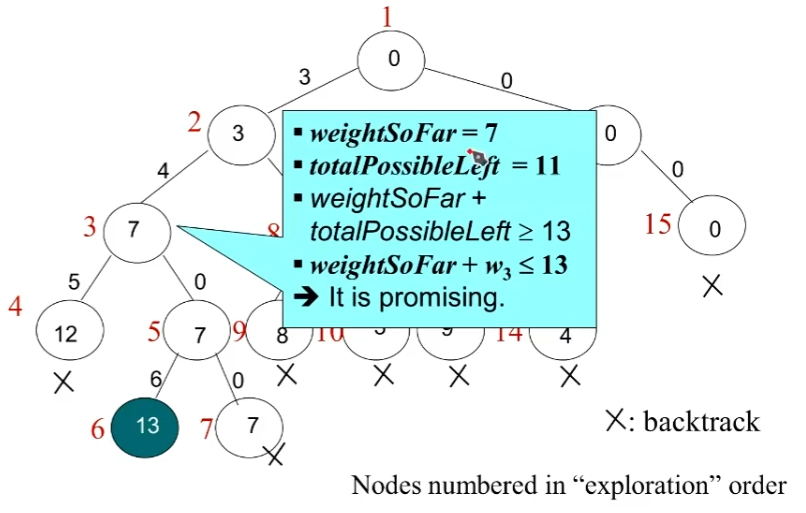
Checknode(v) //v is a nodeif(promising(v))if(aSolutionAt(v))output the solutionelse //expand the nodefor each child u of vChecknode(u)
promising(v)检查v代表的部分解是否还有可能产生有效的解。aSolutionAt(v)检查v代表的部分解是否解决了问题。
那具体到底是如何判断有没有希望的?



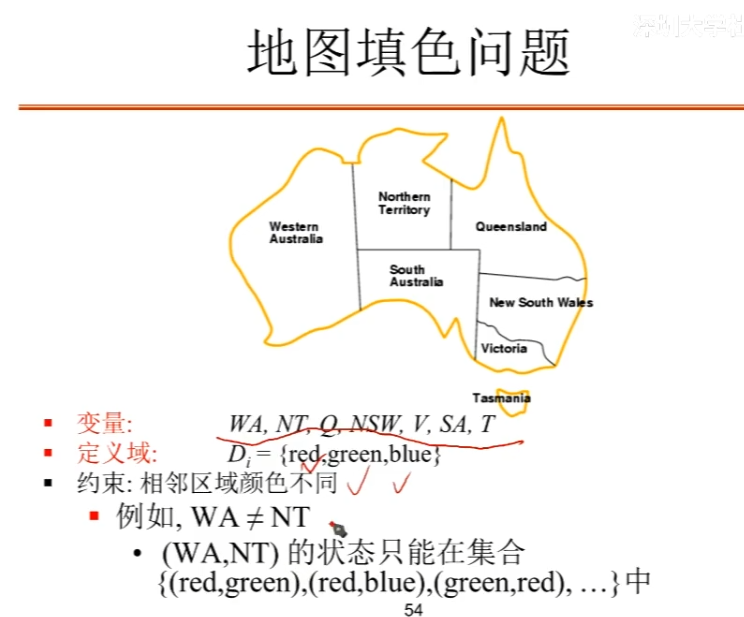
地图填色问题
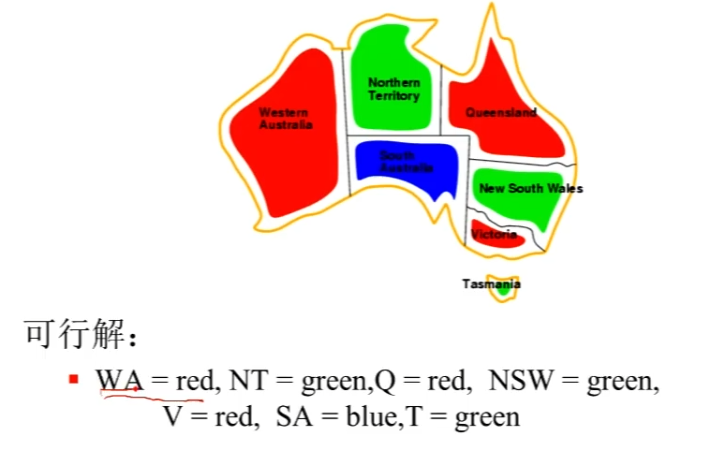
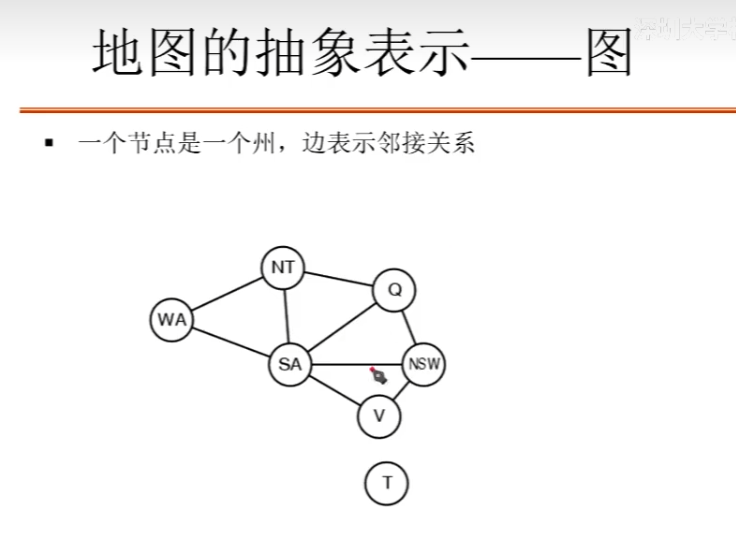

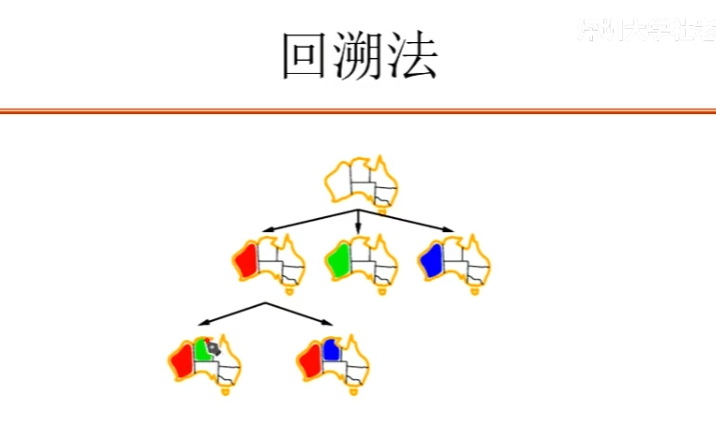
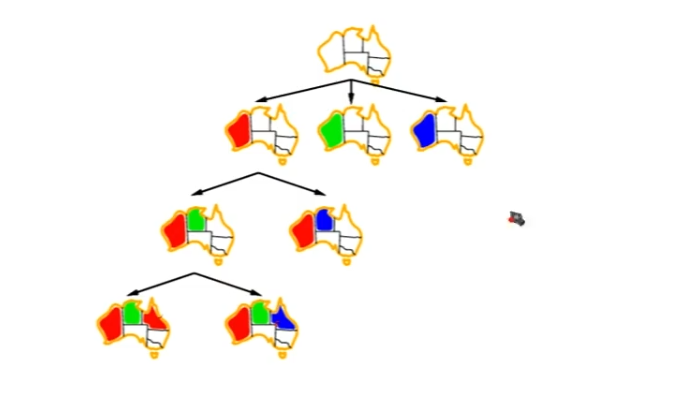
我们要想办法让这个树的规模变小,提高效率。