1.4.1梯度下降

4.1、梯度下降的概念

※【总结一句话】：系统通过自动的调节参数w和b的值，得到最小的损失函数值J。

如下：是梯度下降的概念图。

• 我们有一个损失函数 J(w,b)，包含两个参数w和b（你可以想象成J(w,b) = w*x + b） ，我们想要找到最合适的w和b，尝试最小化损失函数 J(w,b)的值

• ”梯度下降“：梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

• 它还适用于有多个参数的（如图：w1~ wn，b） ：梯度下降的任务是调节w1 ~ wn 和 参数 b 的值，最小化损失函数的值

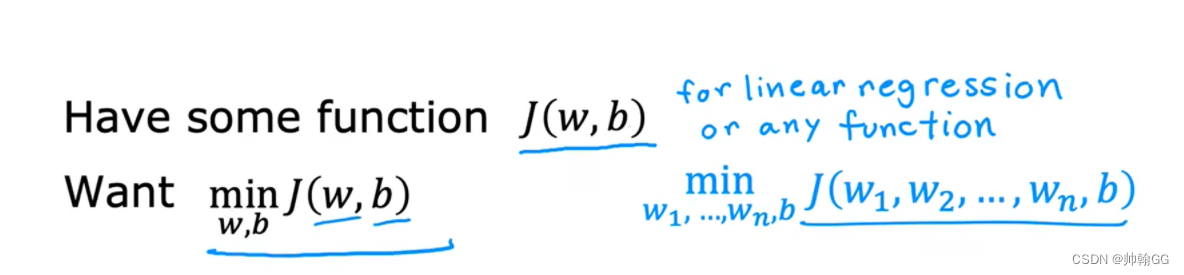
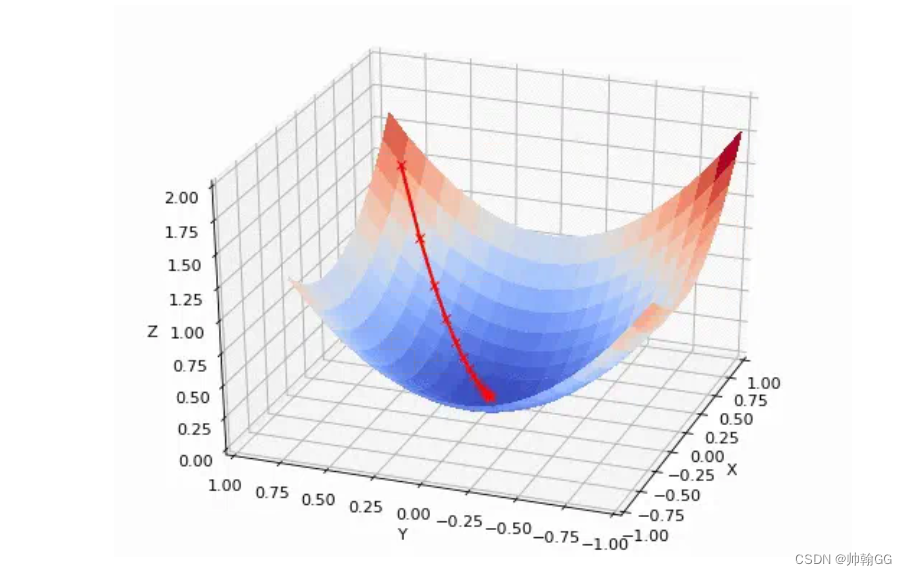
• 梯度下降法是用来计算损失函数最小值的。它的思路很简单，想象在山顶放了一个球，一松手它就会顺着山坡最陡峭的地方滚落到谷底：

4.2、梯度下降概述

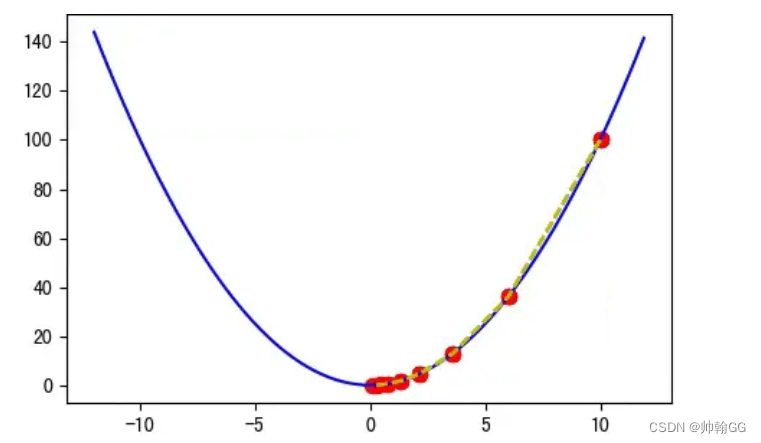
• J（w,b） = wx + b ： 我们开始的时候w和b可以设置为任意值。（这里我们设置 w=0 , b = 0）
• “梯度下降”要做的就是：通过迭代不断的调整 w和b 的值，去尽量的降低损失函数J(w,b)
• 直到我们的损失函数J(w,b) 达到/接近 “谷底”/最小值
• 【※注意】 ：损失函数可能不仅仅是一个如右图的抛物线，也可能是“高尔夫球场图”，这样的话minimum最小值的个数就不仅仅是一个了

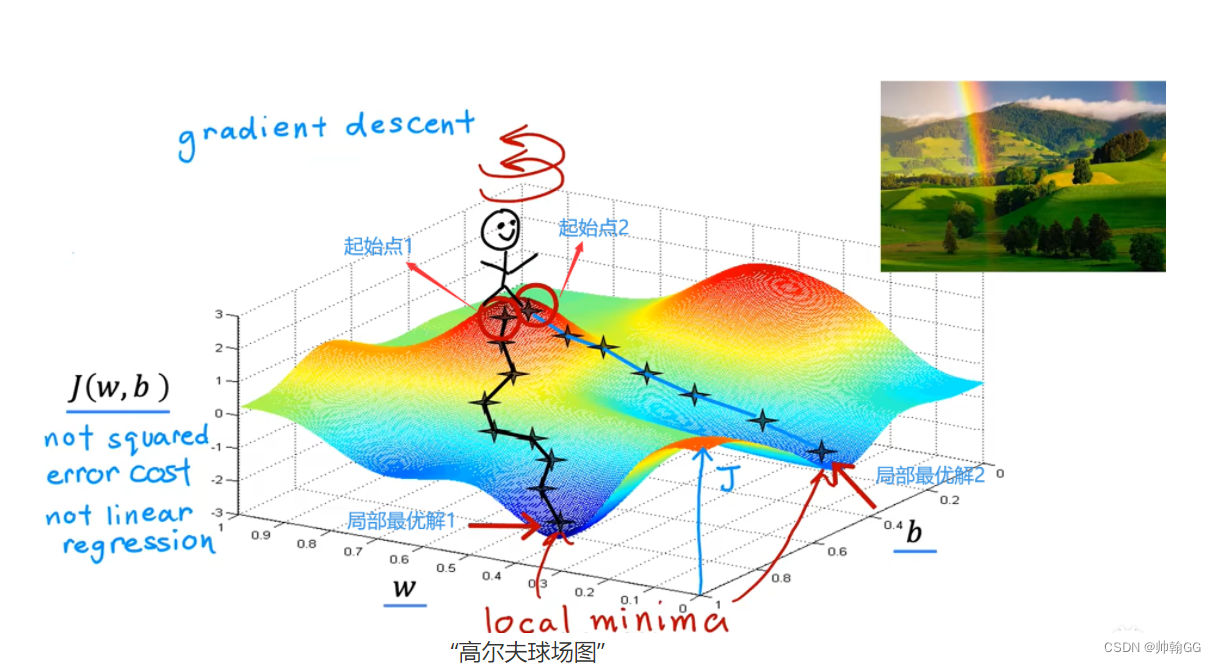
“高尔夫球场图”

• 图中XYZ轴分别代表：W，b ， 损失函数 J(w,b)的值

• 他不是一个 “平方误差损失函数”（线性回归使用 平方误差损失函数）图，因为 “平方误差损失函数”常常以抛物线 / 吊床 的形状结束

• 这个小人站在哪的起始点取决于你选择的参数w 和 b的起始值

• 两个谷底最低点都是局部最优解

1.4.2 理解梯度下降+梯度下降偏导的意义+α学习率

• 图解定义：

• 对梯度下降公式算法的解读：
  • 其中参数 w和b 是一个同步进行 修改/微调 的。（同步进行，就是计算w和b的更新的两个公式是同步计算 的）
  • 重复以上两个公式，直到达到结果收敛为止
  • 在收敛重复这个公式的过程中，在计算tmp_w 和tmp_b中 的w是上一次迭代的w的值，只有tmp_w 和tmp_b都计算完成才会进行更新
• 你可能存在疑问：为什么不要用中间值 tmp_w 和wmp_b，直接就是 w = w - α…;b= b - α…不行吗？？？
  • 答：你提问的很好。但是在这个梯度下降w，b迭代执行过程中，w和b同时参与了w,b的计算。
  • 简单的说如下图，以W为例，加入在第i次迭代的情况下：
    • 在第i次迭代的情况下执行完第一步w = w -0.2 后（假设这时候 J(w,b) = 0.2），
    • 执行第二步 b = b - J(w,b) 的时候,你想放 执行w = w -0.2 更新之前的值 or 更新之后的值？？？
    • 每一次迭代，在这第i次中，w 和 b对应的是第i -1次的值，在第i次迭代结束时才一起更新
    • 如果不借用中间值 tmp_w 和 tmp_b，那么w 和 b 的最终值 就会受到影响
    • 

为了方便理解α（学习率），我们这里把b设置为0，只考虑有w的一维情况

• 其中α：称为学习率（粉色框内容），通常这个值在 0~1 之间，是控制w和b的调参步长

  • 合适：

  过程解释：

  红框中：是求w的偏导，这里求完偏导知道是>0

  α永远是 大于0 小于1 的数

  然后w = w - α（正数） ====> w变小

  所以就实现了微调

  

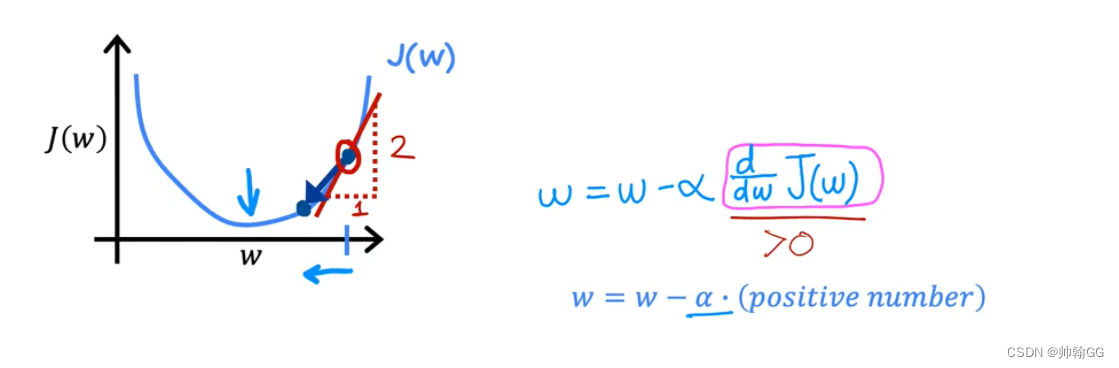
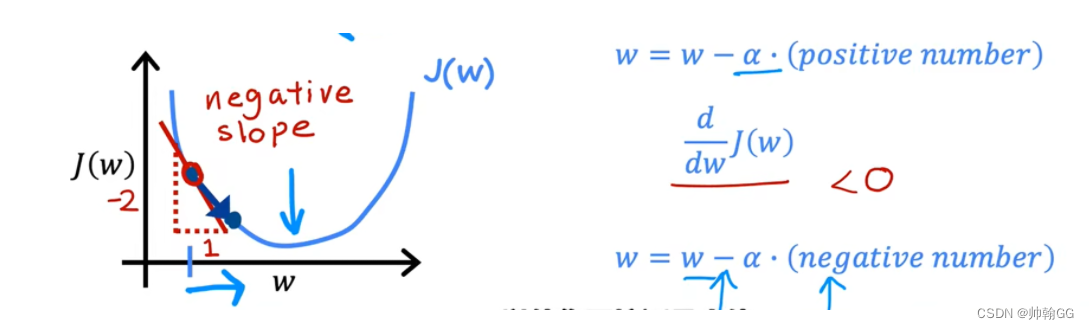
  当W的偏导< 0 时：
  红框中：是求w的偏导，这里求完偏导知道是<0

  α永远是 大于0 小于1 的数

  然后w = w - α（负数） ====> w变大

  所以就实现了微调.

  

  • 如果α非常大：那么这个是一个非常激进的梯度下降的过程，步长会非常大，反而会越过谷底，不断上升：+

  • 动图地址
    

  吴恩达老师的解释：

  ​ 如果α过大/过大的步长：

  ​ 会导致超过 ， 并且从来不会达到最小值。

  ​ 不能直线收敛，甚至是发散

• 如果α非常小：比如 α = 0.0001 就过于小了，迭代 20 次后离谷底还很远，实际上 100 次后都无法到达谷底：

  梯度下降会起作用，但是需要很长的时间

• 动图地址
  

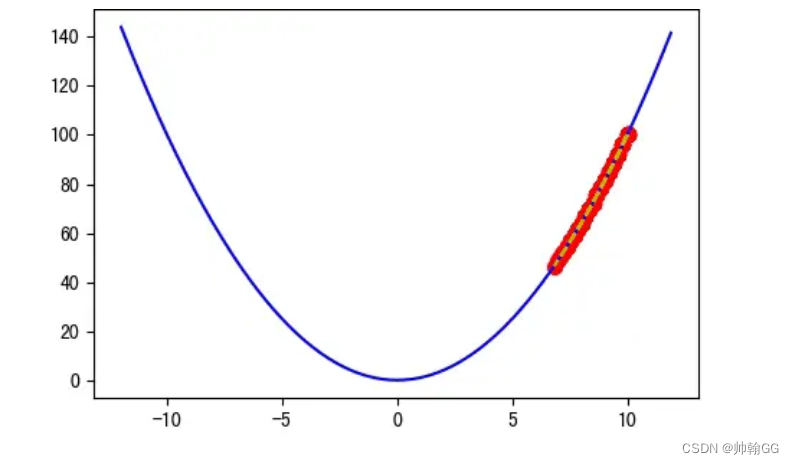
吴恩达的解释：

​ 如果α 步长太小，会实现收敛，但是这个收敛的过程会很慢很慢

• **总结：**不同的步长α ，随着迭代次数的增加，会导致被优化函数f(x) 的值有不同的变化：

关于α选择以及判定的 详细内容看: 2.2.3机器学习—— 判定梯度下降是否收敛 + α学习率的选择

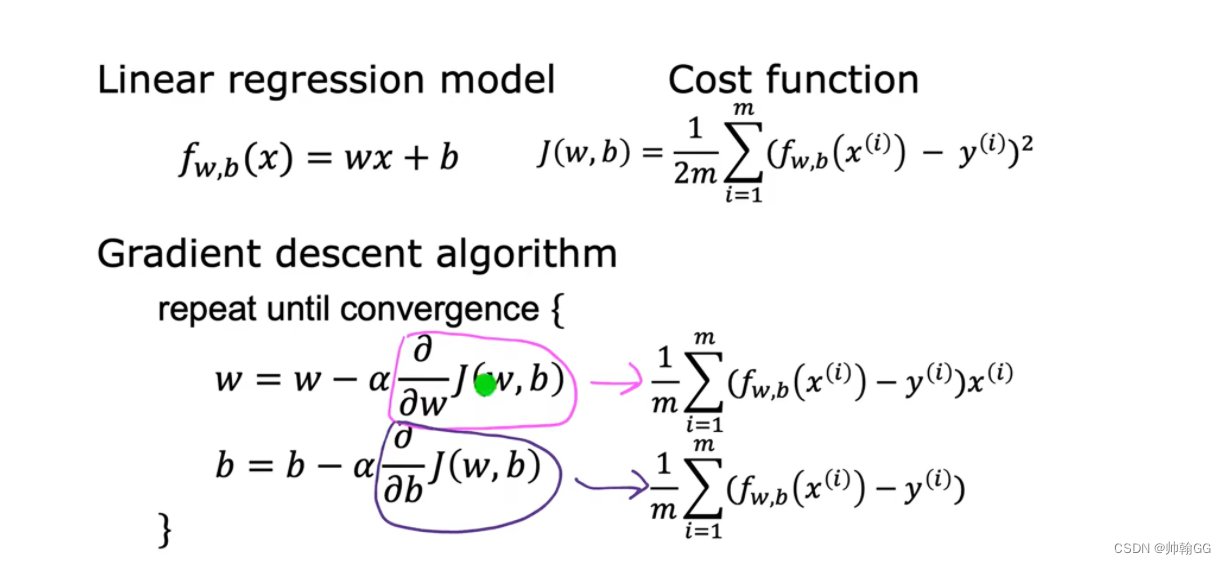
1.4.3 用于线性回归的梯度下降

• 公式推到来源：

  

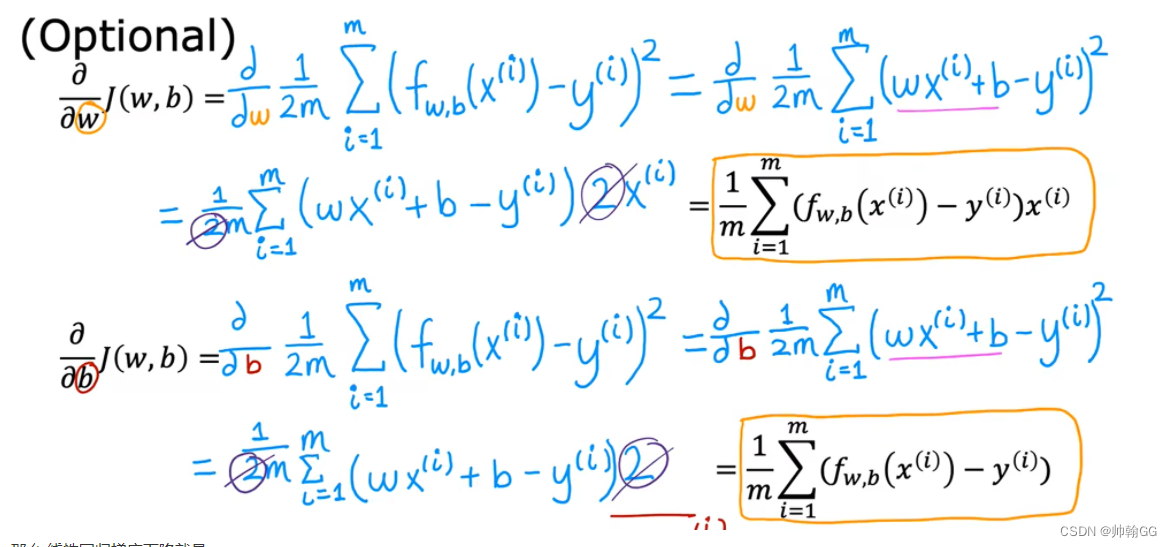
• 那么 线性回归梯度下降就是：

重复对w 和 b 执行更新直到收敛

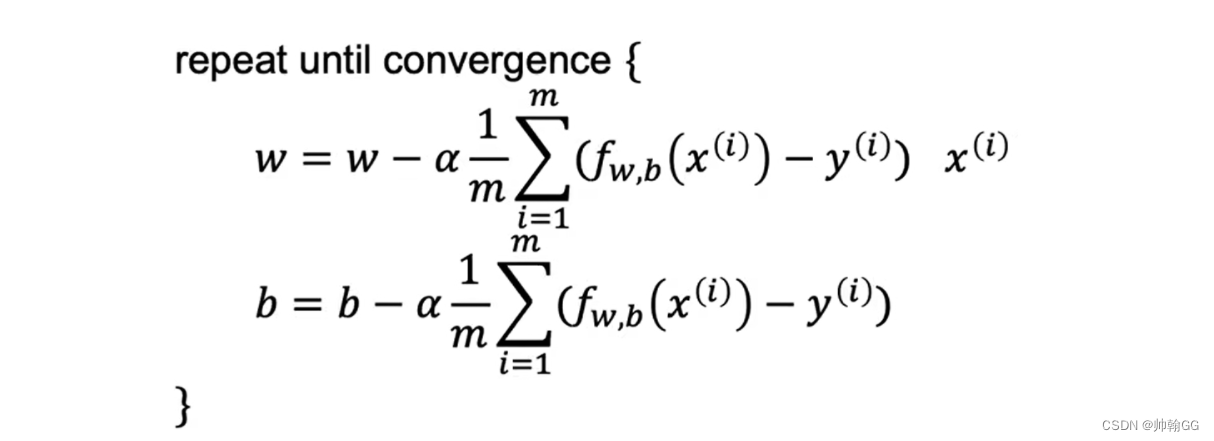
• 当使用线性回归的平方误差损失函数时，全局只有一个最低点

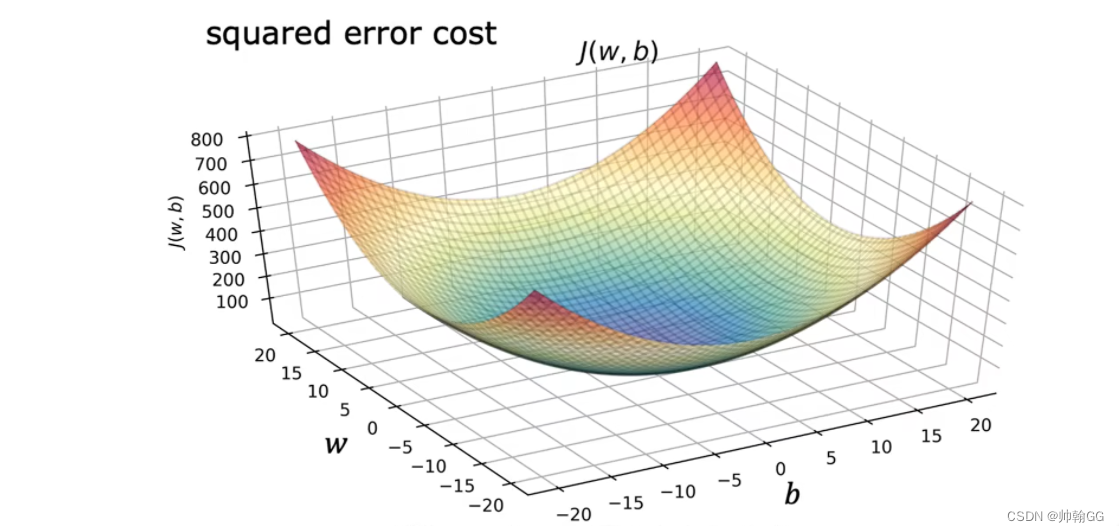
• 当使用非平方误差函数时，就是非线性回归梯度下降的时候就会出现 >=1 的局部最优解

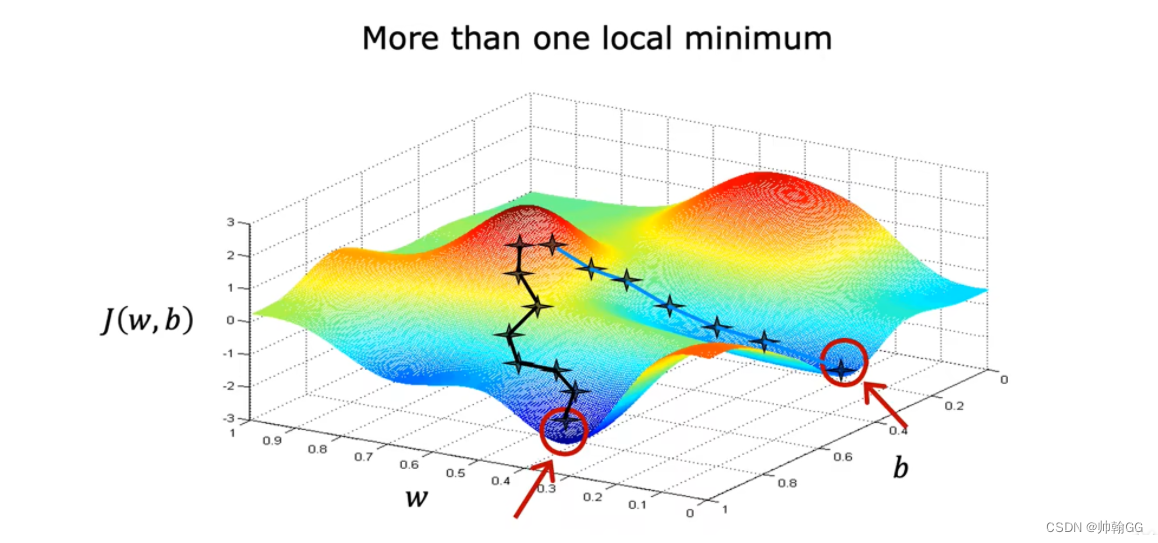
1.4.4 线性回归的梯度下降的应用

• 等高线最中心那个圈是 损失函数值最小的点，Cost值越小，说明线性回归的拟合越好，直到我们达到全局最小值
• 比如当 Size in feet 是1250 ，对应的回归预测值是 250 K

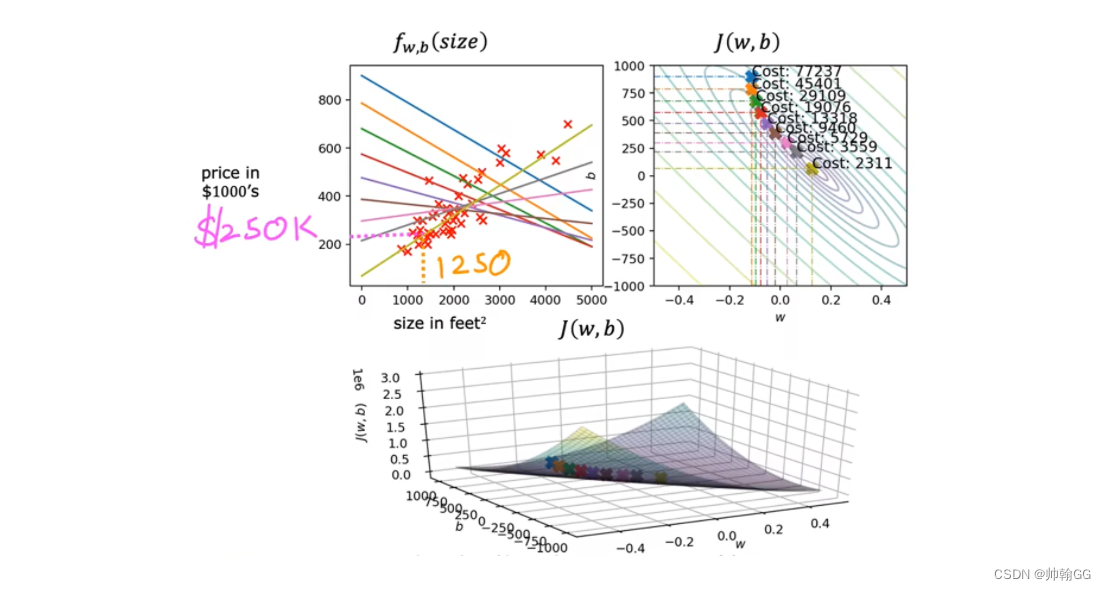
• “批量梯度下降”：每一次的梯度下降使用的是全部的训练的数据：
• 当计算 w 和 b 的偏导时，我们从 1 ~ m 所有的数据都计算上，然后相加求平均

※1.4.5 线性回归的梯度下降函数的代码实现

1、求损失函数

求损失函数代码如下：

def compute_cost(x, y, w, b): """Computes the cost function for linear regression.Args:x (ndarray (m,)): Data, m examples y (ndarray (m,)): target valuesw,b (scalar)    : model parameters  Returnstotal_cost (float): The cost of using w,b as the parameters for linear regressionto fit the data points in x and y"""# number of training examplesm = x.shape[0] cost_sum = 0 for i in range(m): f_wb = w * x[i] + b   cost = (f_wb - y[i]) ** 2  cost_sum = cost_sum + cost  total_cost = (1 / (2 * m)) * cost_sum  return total_cost

2、求偏导 / 梯度

※求偏导代码如下：

def compute_gradient(x, y, w, b): """Computes the gradient for linear regression Args:x (ndarray (m,)): Data, m examples y (ndarray (m,)): target valuesw,b (scalar)    : model parameters  Returnsdj_dw (scalar): The gradient of the cost w.r.t. the parameters wdj_db (scalar): The gradient of the cost w.r.t. the parameter b     """# Number of training examplesm = x.shape[0]    dj_dw = 0dj_db = 0for i in range(m):  f_wb = w * x[i] + b dj_dw_i = (f_wb - y[i]) * x[i] dj_db_i = f_wb - y[i] dj_db += dj_db_idj_dw += dj_dw_i dj_dw = dj_dw / m dj_db = dj_db / m return dj_dw, dj_db

3、梯度下降函数

def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function): """Performs gradient descent to fit w,b. Updates w,b by taking num_iters gradient steps with learning rate alphaArgs:x (ndarray (m,))  : Data, m examples y (ndarray (m,))  : target valuesw_in,b_in (scalar): initial values of model parameters  alpha (float):     Learning ratenum_iters (int):   number of iterations to run gradient descentcost_function:     function to call to produce costgradient_function: function to call to produce gradientReturns:w (scalar): Updated value of parameter after running gradient descentb (scalar): Updated value of parameter after running gradient descentJ_history (List): History of cost valuesp_history (list): History of parameters [w,b] """w = copy.deepcopy(w_in) # avoid modifying global w_in# An array to store cost J and w's at each iteration primarily for graphing laterJ_history = []p_history = []b = b_inw = w_infor i in range(num_iters):# Calculate the gradient and update the parameters using gradient_functiondj_dw, dj_db = gradient_function(x, y, w , b)     # Update Parameters using equation (3) aboveb = b - alpha * dj_db                            w = w - alpha * dj_dw                            # Save cost J at each iterationif i<100000:      # prevent resource exhaustion J_history.append( cost_function(x, y, w , b))p_history.append([w,b])# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters/10) == 0:print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e}  ",f"w: {w: 0.3e}, b:{b: 0.5e}")return w, b, J_history, p_history #return w and J,w history for graphing

※※关于α选择以及判定的 详细内容看: 2.2.3机器学习—— 判定梯度下降是否收敛 + α学习率的选择