有不会的题可以后台问我的哦,看见了就会回。祝大家期末心想事成。
数据库大题显而易见就只有几类,大家可以根据老师平时讲解的例题对应去解决一类型的题目。
前提知识;
候选码==候选键==关键字==键==码
关系代数:(1)传统:交、并、差、笛卡尔积(2)专门:选择、投影、连接、除
关系演算:并、差、选择、投影、笛卡尔积
SQL:select */列名/表达式/函数/常量 from 表名/视图 where 条件
insert、update、delete
E-R图:实体型、属性、关系
一:关系代数和关系演算的转换
这个题型变化大,举个例子
查询信息系(IS系)全体学生
关系代数:
关系演算:
t[5]中5的含义是IS在表中是第几个属性
二:SQL语句
现有关系数据库如下:
学生(学号,姓名,性别,专业)
课程(课程号,课程名,学分)
学习(学号,课程号,分数)
用SQL语句实现下列1—5小题
1. 检索所有选修了课程号为“C112”的课程的学生的学号和分数;
2. 检索“英语”专业学生所学课程的信息,包括学号、姓名、课程名和分数;
3. 检索“数据库原理”课程成绩高于90分的所有学生的学号、姓名、专业和分数;
4. 检索没学课程号为“C135”课程的学生信息,包括学号,姓名和专业;
5. 检索至少学过课程号为“C135”和“C219”的课程的学生的信息,包括学号、姓名和专业。
答案:
1.
SELECT 学号,分数 FROM 学习 WHERE 课程号=’C112’
2.
SELECT 学生.学号,姓名,课程名,分数
FROM 学生,学习,课程
WHERE 学习.学号=学生.学号 AND 学习.课程号=课程.课程号 AND 专业=’英语’
3.
SELECT 学生.学号,姓名,专业,分数
FROM 学生,学习,课程
WHERE 学生.学号=学习.学号 AND 学习.课程号=课程.课程号 AND分数>90 AND 课程名=‘数据库原理’
4.
SELECT 学号,姓名,专业
FROM 学生
WHERE 学号 NOT IN (1分)
(SELECT 学号 FROM 学习 WHERE 课程号=‘C135’)
5.
SELECT 学号,姓名,专业 FROM 学生 WHERE 学号 IN
(SELECT X1.学号 FROM 学习 X1,学习 X2 WHERE X1.学号=X2.学号 AND X1.课程号=‘C135’AND X2.课程号=‘C219’)
三:E-R图与关系模式的转换
设有如下教学环境,一个班级有多名学生,一个学生只属于一个班级。一个学生可以选修若干门课程,每门课若干学生选修,学生选修每门课有一个成绩。一门课程只有一位教师讲授,一名教师可以讲投多门课,每位教师属于一个教研室,一个数研室有若干教师。(前面是描述的实体和联系,后面描述的是属性)其中班级由班级编号、班级名称等属性描述;学生由学号、姓名等属性描述;课程由课程编号、课程名称等属性描述;教师由教师编号、教师姓名、教师地址等属性描述;教研室由教研室编号、教研室名称等属性描述。
1、根据上述语义画出ER图,要求在图中画出属性并注明联系的类型。
2、将ER模型转换成关系模式,并指出每个关系模式的主键和外键。(1)
(2)主键红色,外键蓝色
学生(学号,姓名,班级编号)学生与班级多对一
班级(班级编号,班级名称)
课程(课程编号,课程名称,教师编号)课程与教师多对一
教师(教师编号,教师姓名,教师地址,教研室编号)教师与教研室多对一
教研室(教研室编号,教研室名称)
选修(学号,课程号(既是主键,又是外键),成绩)学生和课程是多对多的关系,所以需要介入选修表
四:候选码、函数依赖、范式
现有如下关系模式:借阅(图书编号,书名,作者名,出版社,读者编号,读者姓名,借阅日期,归还日期),基本函数依赖集F={图书编号→(书名,作者名,出版社),读者编号→读者姓名,(图书编号,读者编号,借阅日期)→归还日期}
(1)读者编号是候选码吗?(2分)
(2)写出该关系模式的主码。(2分)
(3)该关系模式中是否存在非主属性对码的部分函数依赖?如果存在,请写出一个。(2分)
(4)该关系模式满足第几范式?并说明理由。(4分)
答案:
(1)不是(2分)。
(2)(图书编号,读者编号,借阅日期)(2分)
(3)存在(1分)。(图书编号,读者编号,借阅日期)→书名、(图书编号,读者编号,借阅日期)→作者名、(图书编号,读者编号,借阅日期)→出版社、(图书编号,读者编号,借阅日期)→读者姓名(1分,四个函数依赖任选一个即可)
(4)1NF。因为存在非主属性对码的部分函数依赖。
五:求闭包、函数依赖
设关系模式R(ABCD),F是R上成立的FD集,F{A→B,B→C}
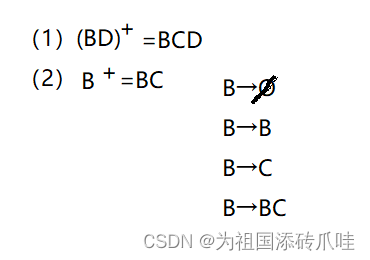
(1)试写出属性集BD的闭包(BD)+
(2)是写出所有左部是B的函数依赖
六:求候选码和关系分解
设有关系模式R(运动员编号、比赛项目、成绩、比赛类别、比赛主管),如果规定:每个运动员每参加一个比赛项目,只有一个成绩;每个比赛项目只属于一个比赛类别;每个比赛类别只有一个比赛主管。试回答下列问题:
①根据上述规定,写出模式R的基本FD和码;
②说明R不是2NF的理由,并把R分解成2NF关系模式集;
③进而分解成3NF关系模式集。
七:无损分解、范式级别
设关系模式R(ABCD),在R上有5个相应的FD集及分解:
(1)F=(B→C,D→A,p=(BC,AD)
(2)F=(AB→C,C→A,C→D),p=(ACD,BC)
(3)F=(A-BC, C→AD),p=(ABC,AD)
(4)F=(A→B,B→C,C-D,p=(AB,ACD)
(5)F=(A→B,B→C,C→D,p=(AB,AD,CD)
试对上述5种情况分别回答下列问题:
a、确定R的关键码。
b、是否是无损分解?
c、是否保持FD集?
d、确定p中每一模式的范式级别。解:(1)
a、R的关键码为BD。
b、p不是无损分解。
c、p保持FD集F。
d、p中每一模式已达到BCNF级别。
(2)a、R有两个关键码:AB和BC。
b、p是无损分解。
c、因为acD(F)=(C→A,C→D),Tgc(F)=中(没有非平凡的FD),所以p不保持FD,丢失了AB→C。
d、p中两模式均已达到BCNF级别。
(3)a、R有两个关键码:A和C。
b、p是无损分解。
c、因为TABc(F)=(A→BC,C→A),TD(F)=(A→D),所以p保持FD。
d、在模式ABC中,关键码是A或BC,属性全是主属性,但有传递依赖(A→BC,BC→A),因此模式ABC是3NF,但不是BCNF,而模式AD显然已是BCNF。
(4)a、R的关键码为A。
b、p是无损分解。
c、因为Tab(F)=(A→B,TacD(F)=(A→C,C→D),从这两个依赖集推不出原来的B→C,因此,不保持FD,丢失了B→C。
d、模式AB是BCNF,模式ACD不是3NF,只达到2NF级别。
(5)a、R的关键码为A。
b、p不是无损分解。
c、因为TaB(F)=(A→B,tap(F)=(A→D),Tco(F)=(C→D),从这3个依赖集不能推理得到原来的B→C,因此p不保持FD,丢失了B→C。
d、p中每个模式均是BCNF级别。













![LeetCode[27]移除元素](http://pic.xiahunao.cn/LeetCode[27]移除元素)








)
