写论文的时候需要做一些激活函数的图像，为此将常见的激活函数进行整理汇总了一下，方便后续的复习

激活函数的作用是为让模型处理非线性问题，故次激活函数都是非线性的
生活中，非线性问题占大多数，而模型的训练通常都是线性可分的函数，通过非线性激活函数可以使得模型刚好的处理非线性问题

一、导包

from matplotlib import pyplot as plt
import numpy as np
import mpl_toolkits.axisartist as axisartist

二、sigmoid

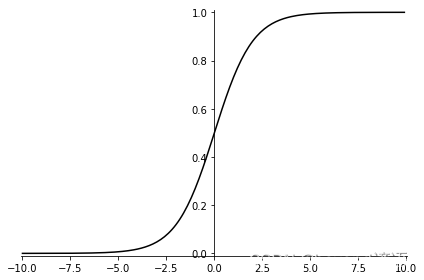
简而言之：通过sigmoid函数可以将函数值转换为0-1之间，从而变成了概率问题，实现不同类别的分类
详细的函数推到可参考博文：四、逻辑回归

大概讲解下代码：
函数 sigmoid(x) 为sigmoid的表达式

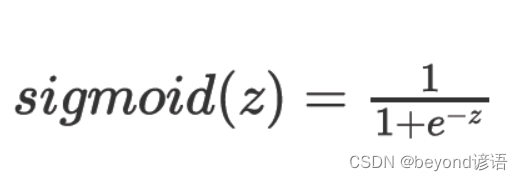
函数 plot_sigmoid() 根据函数表达式进行绘图

x = np.arange(-10, 10, 0.1)
X轴从 [-10,10) 中每隔0.1选取一个点，X轴最终为200个数据点

y = sigmoid(x)
把x这些点带入sigmoid函数中得到对应的y值

fig = plt.figure()
生成一个图框，这个图框目前还不能画图，需要在其子图(subplot)或者轴域(Axes)中作图

ax = fig.add_subplot(111)
第一个参数表示行数、第二个参数表示列数、第三个参数表示第几个子图
这里就是一行、一列、第一个子图

ax.spines['top'].set_color('none')
去掉顶部的边框线，这里的none表示啥也没，相当于去掉顶端边框
ax.spines['right'].set_color('none')
同样的道理，去掉右侧的边框
左侧：left、底部：bottom

ax.spines['left'].set_position(('data', 0))
这里的data表示通过 给定的值(这里是0) 来进行设置坐标轴的位置
这里的0可以理解为：平移y轴到x轴的什么位置，这里就是平移y轴到x轴的0刻度处
当然参数也可以设置为axes，表示按百分比进行偏移y轴，也就相当于按多少进行平分x轴；后一个参数为0.5，相当于平分x轴
ax.spines['left'].set_position(('axes', 0.5))和ax.spines['left'].set_position(('data', 0))是等价的关系

ax.plot(x, y, 'k-')
根据之前得到的x和y值进行绘制，前提x和y的个数是一致的，得一一对应才行
参数k-，表示颜色为black，使用 - 进行连接
也可以设置其他的，例如：红色，通过 + 这个符号进行连接，最后一个参数可以设置为r+，多动手试试就知道了

plt.xlim([-10.05, 10.05])
x轴的取值范围为 [-10.05,10.05]
plt.ylim([-0.01, 1.01])
y轴的取值范围为 [-0.01,1.01]

plt.tight_layout()
有时，轴标签和标题等会出现重叠、超过正常范围而被截断等情况发生，通过调用该函数即可进行解决

plt.savefig("sigmoid.png")
保存生成的图片，参数为字符串，传入要保存的具体路径

plt.show()
展示生成的图片

def sigmoid(x):return 1. / (1 + np.exp(-x))def plot_sigmoid():x = np.arange(-10, 10, 0.1)y = sigmoid(x)fig = plt.figure()ax = fig.add_subplot(111)ax.spines['top'].set_color('none')ax.spines['right'].set_color('none')ax.spines['left'].set_position(('data', 0))ax.plot(x, y, 'k-')plt.xlim([-10.05, 10.05])plt.ylim([-0.01, 1.01])plt.tight_layout()# plt.savefig("sigmoid.png")plt.show()
if __name__ == "__main__":plot_sigmoid()

二、tanh

函数表达式：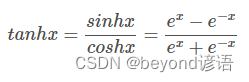
函数 tanh(x) 为tanh的表达式

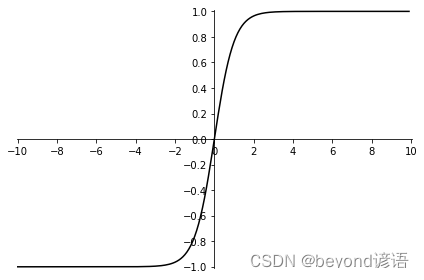
函数 plot_tanh() 绘制tanh函数图像
函数操作都大差不差，根据上面sigmoid激活函数的实现进行类比即可
这里只讲解未出现的函数

ax.set_yticks([-1.0, -0.8, -0.6, -0.4, -0.2, 0, 0.2, 0.4, 0.6, 0.8, 1.0])
设置y轴显示刻度的范围，说白了就是显示y轴的刻度线都有哪几个点
ax.set_xticks([-10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10])
设置x轴显示刻度的范围

def tanh(x):return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))def plot_tanh():x = np.arange(-10.0, 10.0, 0.1)y = tanh(x)fig = plt.figure()ax = fig.add_subplot(111)ax.spines['top'].set_color('none')ax.spines['right'].set_color('none')ax.spines['left'].set_position(('data', 0))ax.spines['bottom'].set_position(('data', 0))ax.plot(x, y, 'k-')plt.xlim([-10.05, 10.05])plt.ylim([-1.01, 1.01])ax.set_yticks([-1.0, -0.8, -0.6, -0.4, -0.2, 0, 0.2, 0.4, 0.6, 0.8, 1.0])ax.set_xticks([-10.0, -8.0, -6.0, -4.0, -2.0, 0.0, 2.0, 4.0, 6.0, 8.0, 10.0])plt.tight_layout()# plt.savefig("tanh.png")plt.show()
if __name__ == "__main__":plot_tanh()

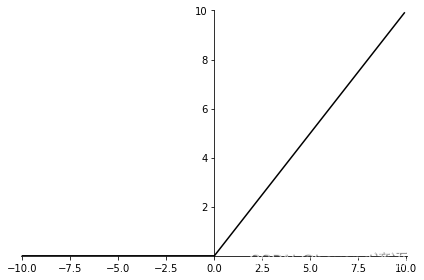
三、relu

函数表达式：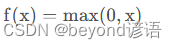
函数操作都大差不差，根据上面sigmoid激活函数的实现进行类比即可

def relu(x):return np.where(x <= 0, 0, x)def plot_relu():x = np.arange(-10, 10, 0.1)y = relu(x)fig = plt.figure()ax = fig.add_subplot(111)ax.spines['top'].set_color('none')ax.spines['right'].set_color('none')ax.spines['left'].set_position(('data', 0))ax.plot(x, y, 'k-')plt.xlim([-10.05, 10.05])plt.ylim([0, 10.01])ax.set_yticks([2, 4, 6, 8, 10])plt.tight_layout()# plt.savefig("relu.png")plt.show()if __name__ == "__main__":plot_relu()

四、elu

函数表达式：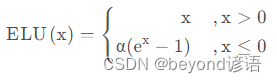
这里α取值为1，当然具体情况具体分析

函数操作都大差不差，根据上面sigmoid激活函数的实现进行类比即可

def elu(x):return np.where(x < 0, 1*(np.exp(x)-1), x)def plot_elu():x = np.arange(-10, 10, 0.1)y = elu(x)fig = plt.figure()ax = fig.add_subplot(111)ax.spines['top'].set_color('none')ax.spines['right'].set_color('none')ax.spines['left'].set_position(('data', 0))ax.spines['bottom'].set_position(('data', 0))ax.plot(x, y, 'k-')#plt.xticks([])ax.set_yticks([-2, 0, 2, 4, 6, 8, 10])plt.tight_layout()# plt.savefig("prelu.png")plt.show()if __name__ == "__main__":plot_elu()

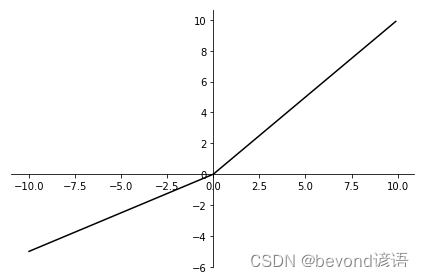
五、prelu

函数表达式：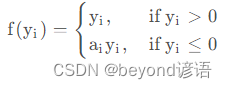
这里的ai取值为0.5，当然具体情况具体分析

函数操作都大差不差，根据上面sigmoid激活函数的实现进行类比即可

def prelu(x):return np.where(x <= 0, 0.5 * x, x)def plot_prelu():x = np.arange(-10, 10, 0.1)y = prelu(x)fig = plt.figure()ax = fig.add_subplot(111)ax.spines['top'].set_color('none')ax.spines['right'].set_color('none')ax.spines['left'].set_position(('data', 0))ax.spines['bottom'].set_position(('data', 0))ax.plot(x, y, 'k-')#plt.xticks([])ax.set_yticks([-6, -4, -2, 0, 2, 4, 6, 8, 10])plt.tight_layout()# plt.savefig("prelu.png")plt.show()if __name__ == "__main__":plot_prelu()