题目

输入一个由0、1组成的矩阵M，请输出一个大小相同的矩阵D，矩阵D中的每个格子是矩阵M中对应格子离最近的0的距离。水平或竖直方向相邻的两个格子的距离为1。假设矩阵M中至少有一个0。
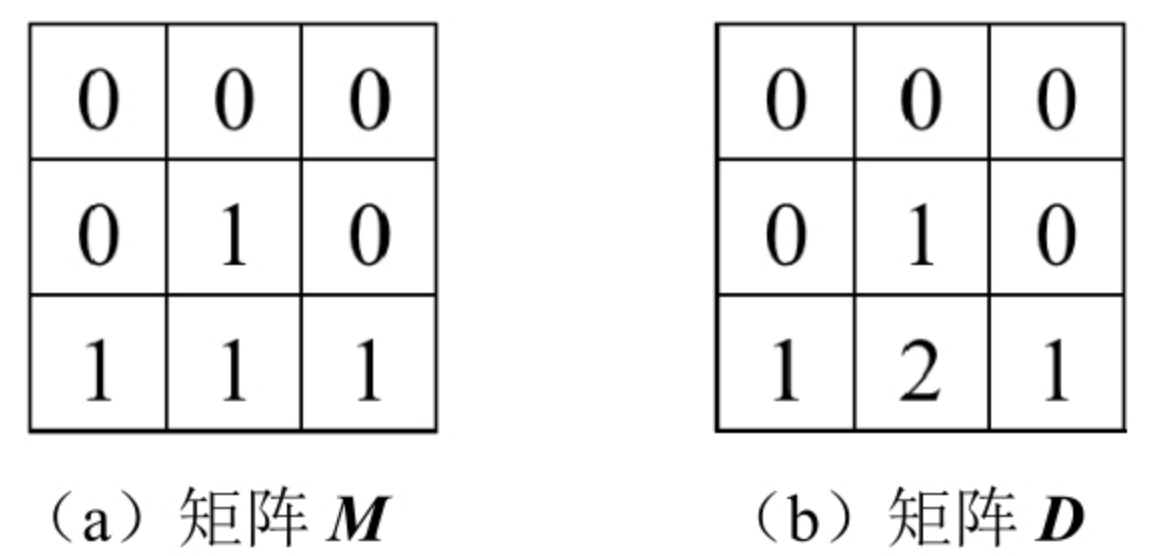
例如，图（a）是一个只包含0、1的矩阵M，它的每个格子离最近的0的距离如（b）的矩阵D所示。M[0][0]等于0，因此它离最近的0的距离是0，所以D[0][0]等于0。M[2][1]等于1，离它最近的0的坐标是（0，1）、（1，0）、（1，2），它们离坐标（2，1）的距离都是2，所以D[2][1]等于2。

分析

这个题目要求计算每个格子离最近的0的距离。根据题目的要求，上、下、左、右相邻的两个格子的距离为1。可以将图看成一个无权图，图中两个节点的距离是连通它们的路径经过的边的数目。由于这个问题与无权图的最近距离相关，因此可以考虑应用广度优先搜索解决。

解

public class Test {public static void main(String[] args) {int[][] matrix = {{0, 0, 0}, {0, 1, 0}, {1, 1, 1}};int[][] result = updateMatrix(matrix);for (int[] item : result) {System.out.println(item[0] + " " + item[1] + " " + item[2]);}}public static int[][] updateMatrix(int[][] matrix) {int rows = matrix.length;int cols = matrix[0].length;int[][] dists = new int[rows][cols];Queue<int[]> queue = new LinkedList<>();for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (matrix[i][j] == 0) {// 先将所有的0当作初始节点添加到队列中queue.add(new int[] {i, j});dists[i][j] = 0;// 离最近的0的距离为0}else {dists[i][j] = Integer.MAX_VALUE;// 先初始化为最大值}}}int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};while (!queue.isEmpty()) {int[] pos = queue.remove();int dist = dists[pos[0]][pos[1]];for (int[] dir : dirs) {int r = pos[0] + dir[0];int c = pos[1] + dir[1];if (r >= 0 && c >= 0 && r < rows && c < cols) {// dists[r][c]初始化为最大值，此处取一个最小值if (dists[r][c] > dist + 1) {dists[r][c] = dist + 1;queue.add(new int[] {r, c});}}}}return dists;}}