对称矩阵是最重要的矩阵之一，其特征值为实数并且拥有一套正交特征向量。正定矩阵的性质则更好。

对称矩阵 Symmetric matrices

包含特殊性质的矩阵，例如 Markov 矩阵，其特征值和特征向量往往拥有一定特性。对称矩阵 $A=A^T$的特征值为实数，具有完全正交的特征向量。这里的“有”，是指可以选出一套完全正交的特征向量（例如在重特征值条件下，可能存在一个平面内向量都可以作为特征向量）。

如果 A 具有 n 个线性无关的特征向量，可以对角化得到 $A=S\Lambda S^{-1}$。而对于对称矩阵，$A=Q\Lambda Q^{-1}=Q\Lambda Q^T$，其中 Q 为正交矩阵，列向量为标准正交基，这个公式本身还显示了矩阵的对称性。矩阵能够进行这种分解，在数学上称为“谱定理”（spectral theorem），将特征值视为“谱”，在物理上称之为“主轴定理”。

实特征值 Real eigenvalues

对于对称矩阵，$A=Q\Lambda Q^{-1}=Q\Lambda Q^T$，可以写作：

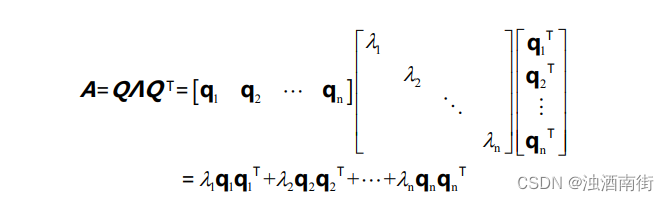
矩阵是 $q_k{q}_k^T=(q_k{q}_k^T/(q_k^T{q}_k))$是朝向向量 $q_k$ 的投影矩阵，所以每一个对称矩阵都是正交投影矩阵的线性组合。这是理解谱定理的另一种方法。

当确认矩阵特征值为实数后，下一个要考虑的问题就是它是正还是负数，因为这影响着微分方程中体系的稳定与否。但是对于大型矩阵，通过计算 $\left|\begin{array}{c}A-\lambda I\end{array}\right|$ 得到特征值进行判定难以实现，即使用 MATLAB 求解，结果也不一定可靠，但 MATLAB可以得到矩阵的主元，而对称阵的主元中正负数的个数与特征值相同，即正主元的数目等于正特征值的数目。

矩阵 A+bI 的特征值比矩阵 A 的特征值大 b，可以通过 A+bI 的主元来了解矩阵 A 的特征值与 b 的大小关系，因此利用这个性质可以估计特征值的状态。

正定矩阵 Positive definite matrices

正定矩阵 A 是特征值都为正数的对称矩阵。它的主元也均为正数。

例如矩阵 A=$\left[\begin{array}{cc}5& 2\\ 2& 3\end{array}\right]$ 。主元为 5 和(detA)/5=11/5。主元都为正数，且本身为对称矩阵，因此 A 是正定矩阵。计算其特征值为：$\left|\begin{array}{c}A-\lambda I\end{array}\right|={\lambda }^2-8\lambda +11=0,\lambda =4\pm \sqrt{5}$ 。

因为主元和特征值都是正的，可以知道正定矩阵的行列式也是正的。但是反之，并不成立。矩阵$\left[\begin{array}{cc}-1& 0\\ 0& -3\end{array}\right]$的行列式也是正的，但不是正定矩阵。

若将行列式作为正定的判据，则要求 n 阶矩阵左上角的所有 k x k（1<= k <= n）子行列式（subdeterminant）数值均为正，矩阵才能确定为正定矩阵。

本讲的内容将之前教授的主元、行列式和特征值的概念结合在了一起，对于正定矩阵这些都是正的，当完全掌握了它们的性质后会推广到非对称矩阵，甚至非方阵。