C#，数值计算，矩阵相乘的源代码与数据可视化

俺玩数学，你玩技巧，俺不如你，佩服佩服！

一、矩阵乘法的基本概念

定义：矩阵 A ∈ Rm×n 和B ∈ Rn×p 的乘积为矩阵C∈ Rm×p 。

限制：矩阵A的列数应该与矩阵B的行数相等。

算法：矩阵A的第一行每个元素分别与B的第一列相乘再求和，得到C矩阵的第一个数；然后A矩阵的第一行再与B矩阵的第二列相乘，得到C矩阵的第二个数；以此类推…

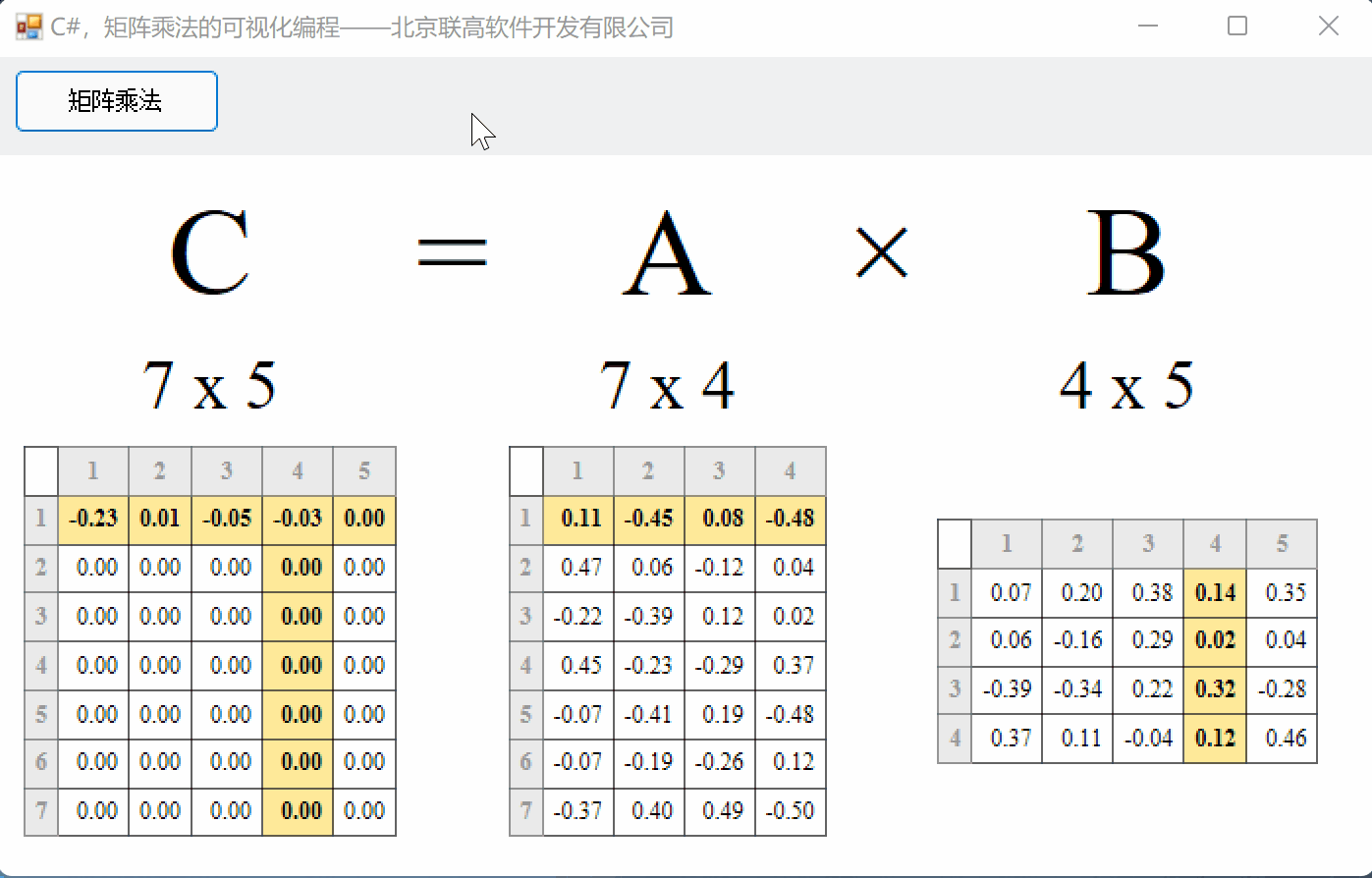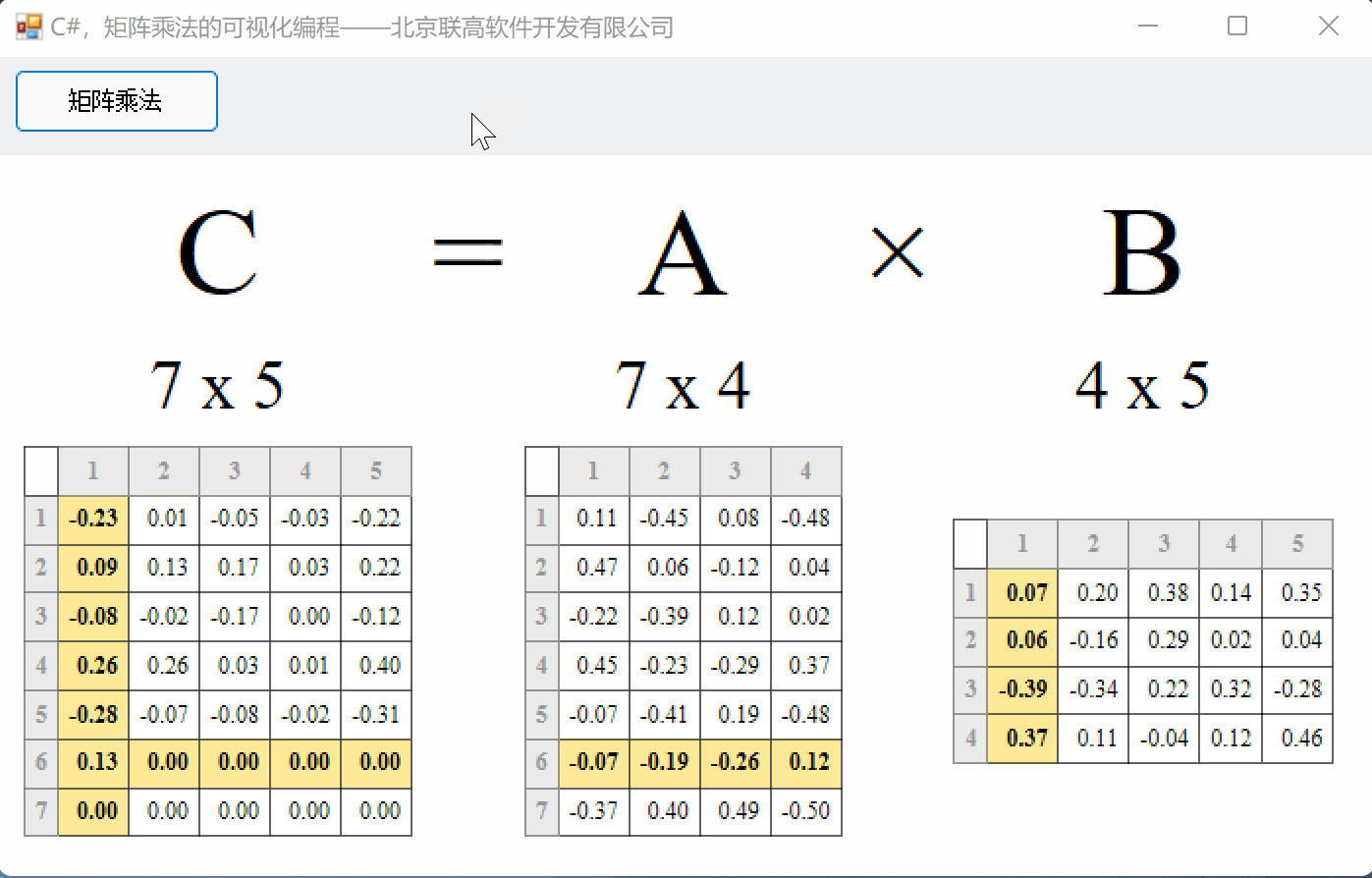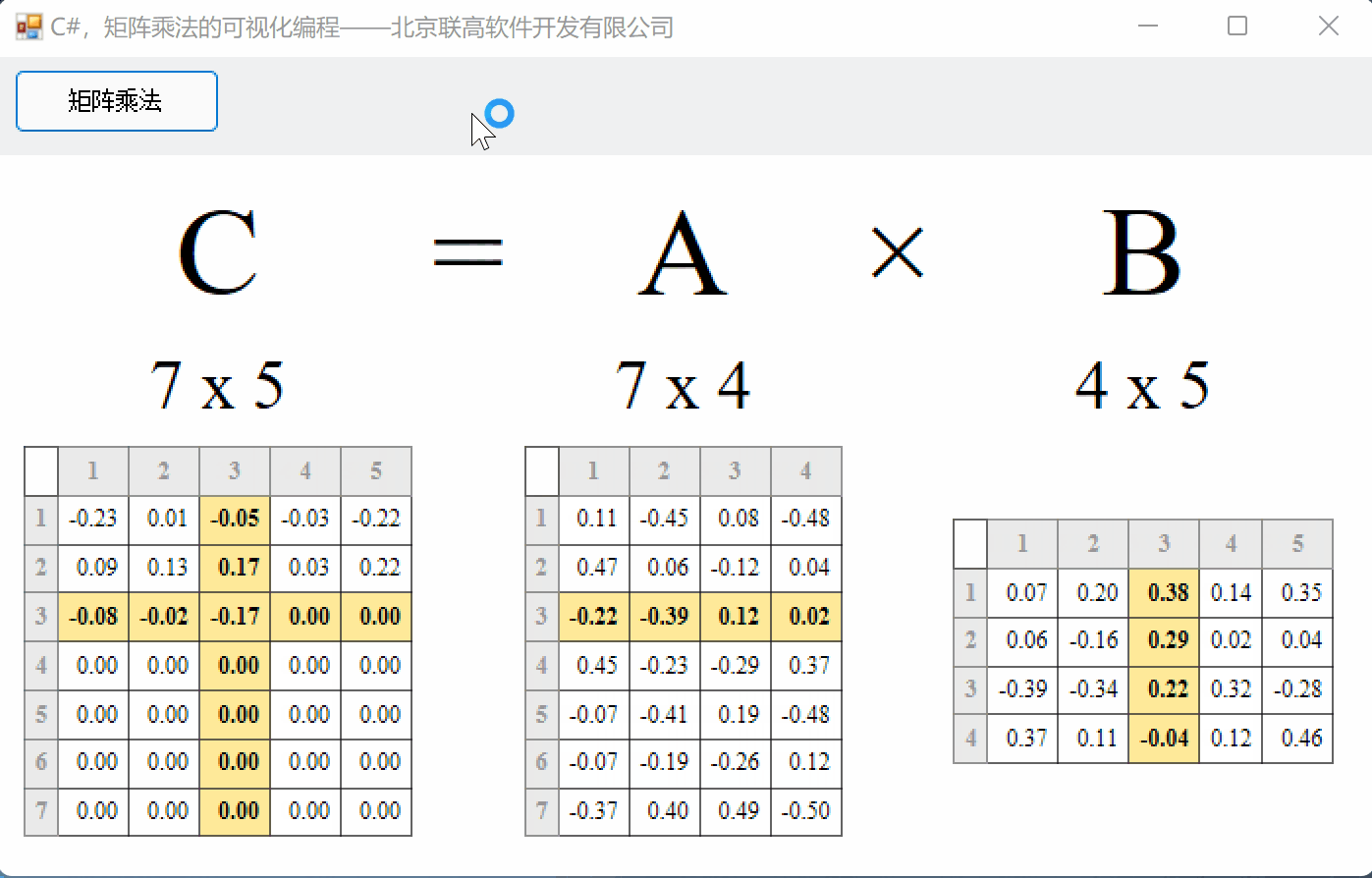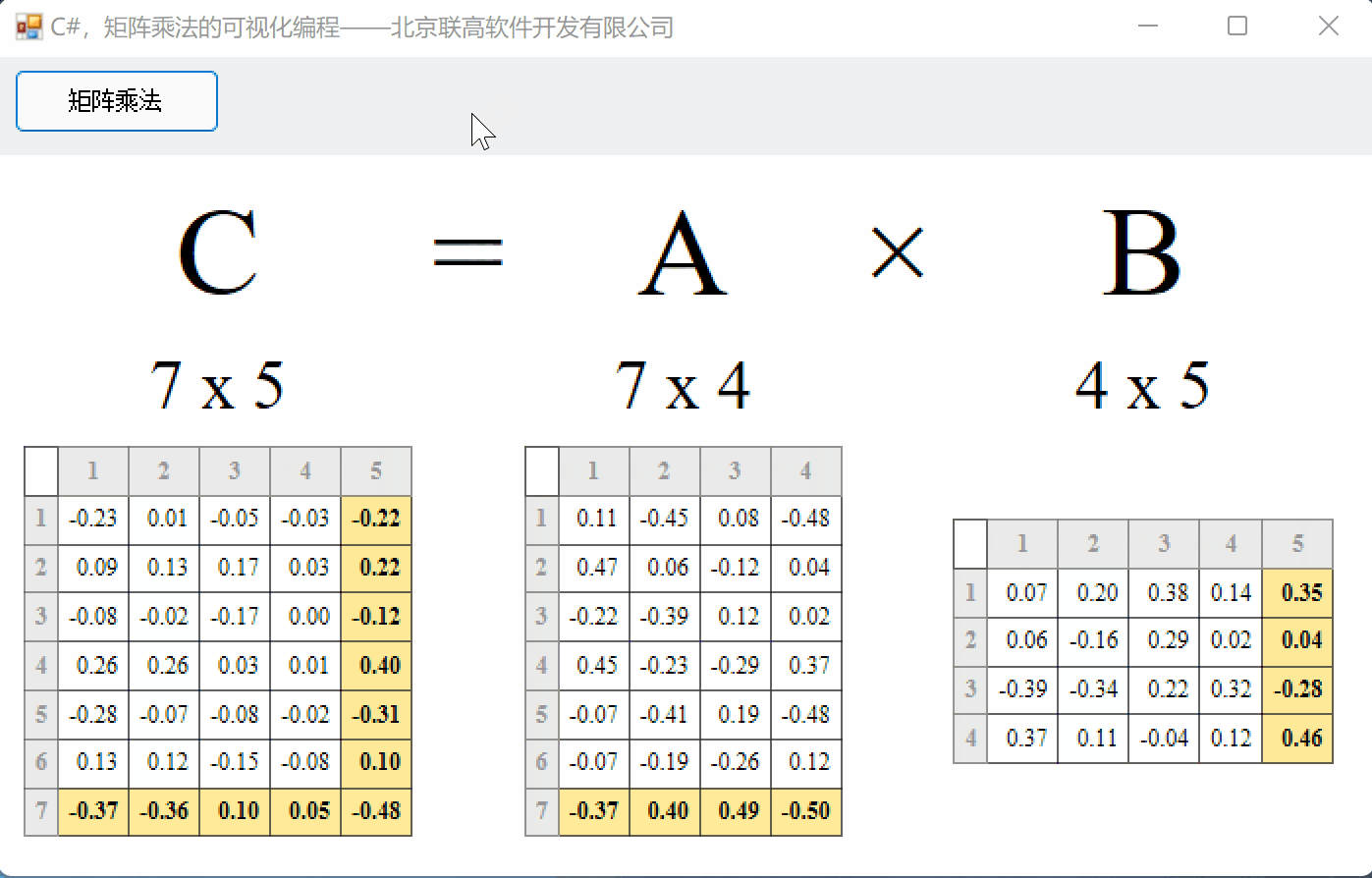
在线性代数中，矩阵在处理不同的概念中扮演着重要的角色。矩阵是数学中按行和列排列的数字、符号或表达式的矩形阵列或表格。我们可以对矩阵执行各种运算，如加法、减法、乘法等。在本文中，您将通过示例详细学习如何将一个矩阵与另一个矩阵相乘，其算法、公式、2×2和3×3矩阵乘法。

矩阵乘法定义

矩阵乘法，也称为矩阵乘积和两个矩阵的乘法，产生一个矩阵。这是一种二进制运算。

如果A和B是两个矩阵，则两个矩阵A和B的乘积表示为：

X=AB

因此，两个矩阵的乘积就是两个矩阵之间的点积。

矩阵乘法算法

近年来，在矩阵乘法算法领域有大量的工作，因为它在许多领域都有应用。有四种类型的算法：

迭代算法

分治算法

亚立方算法

并行和分布式算法

这主要用于各种编程语言，如C、Java等，用于在线乘法。最常见的是2×2、3×3和4×4矩阵乘法。

运算是二进制的，集合中的条目定义了加法、减法、乘法和除法运算。这些运算与实数和有理数的相应运算相同。

虽然矩阵有很多应用，但本质上，矩阵的乘法是线性代数中的一种运算。线性映射包括标量加法和乘法，由矩阵乘法表示。

人们还可以在网格上找到各种各样的算法。这种类型的算法被设计为最小化标准阵列算法的固有效率，其中来自2个不同矩阵的数据的到达可能存在延迟。

矩阵乘法规则

从上面定义的公式和过程中，我们可以写出以下矩阵乘法的规则和属性。

如果A的列数等于B的行数，则定义两个矩阵A和B的乘积。

如果定义了AB，则无需定义BA

如果A和B都是相同阶的方阵，则AB和BA都被定义。

如果AB和BA都定义了，则不必AB=BA。

如果两个矩阵的乘积是零矩阵，则其中一个矩阵不必是零矩阵。

二、矩阵类源代码

#define ANIMATEusing System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Math.Basic
{public partial class Matrix{/// <summary>/// 行数量/// </summary>public int Row { get; set; } = 0;/// <summary>/// 列数量/// </summary>public int Column { get; set; } = 0;/// <summary>/// 数据（二维数值）/// </summary>private double[,] Data { get; set; } = null;/// <summary>/// 取值this的重载/// </summary>/// <param name="y"></param>/// <param name="x"></param>/// <returns></returns>public double this[int row, int column]{set { Data[row, column] = value; }get { return Data[row, column]; }}/// <summary>/// 构造函数（按二维数组）/// </summary>/// <param name="d"></param>public Matrix(double[,] d){Row = d.GetLength(0);Column = d.GetLength(1);Data = new double[Row, Column];for (int y = 0; y < Row; y++){for (int x = 0; x < Column; x++){Data[y, x] = d[y, x];}}}/// <summary>/// 构造函数(方阵)/// </summary>/// <param name="row"></param>/// <param name="column"></param>public Matrix(int row, int column){Row = row;Column = column;Data = new double[row, column];}/// <summary>/// 随机矩阵（用于演示）/// </summary>/// <param name="row"></param>/// <param name="column"></param>/// <param name="rnder"></param>public Matrix(int row, int column, Random rnder){Row = row;Column = column;Data = new double[row, column];for (int y = 0; y < Row; y++){for (int x = 0; x < Column; x++){Data[y, x] = (rnder.NextDouble() - 0.5);}}}/// <summary>/// 乘号的重载（乘法）/// </summary>/// <param name="a"></param>/// <param name="b"></param>/// <returns></returns>public static Matrix operator *(Matrix a, Matrix b){Matrix c = new Matrix(a.Row, b.Column);for (int y = 0; y < c.Row; y++){for (int x = 0; x < c.Column; x++){c[y, x] = 0.0;for (int k = 0; k < a.Column; k++){c[y, x] += a[y, k] * b[k, x];}
#if ANIMATE// 生成演示片段slides.Add(Slide(a, b, c, y, x));
#endif}}return c;}}
}

In linear algebra, matrices play an important role in dealing with different concepts. A matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns in mathematics. We can perform various operations on matrices such as addition, subtraction, multiplication and so on. In this article, you will learn how to multiply a matrix by another matrix, its algorithm, formula, 2×2 and 3×3 matrix multiplication with examples in detail.

Matrix Multiplication Definition
Matrix multiplication, also known as matrix product and the multiplication of two matrices, produces a single matrix. It is a type of binary operation.

If A and B are the two matrices, then the product of the two matrices A and B are denoted by:

X = AB

Hence, the product of two matrices is the dot product of the two matrices.

Algorithm for Matrix Multiplication
There has been a significant amount of work in recent years in the field of matrix multiplication algorithms as it has found its application in many areas. There are four types of algorithms:

Iterative Algorithm
Divide and conquer algorithm
Sub-cubic algorithms
Parallel and distributed algorithms
This is majorly used in various programming languages such as C, Java, etc., for online multiplication. The most common are 2×2, 3×3 and 4×4, multiplication of matrices.

The operation is binary with entries in a set on which the operations of addition, subtraction, multiplication, and division are defined. These operations are the same as the corresponding operations on real and rational numbers.

Although there are many applications of matrices, essentially, multiplication of matrices is an operation in linear algebra. The linear mapping, which includes scalar addition and multiplication, is represented by matrix multiplication.

One can also find a wide range of algorithms on meshes. This type of algorithm is designed to minimize the inherent inefficiency of standard array algorithms where there can be a delay in the arrival of data from 2 different matrices.

Matrix multiplication Rules
From the above defined formula and procedure, we can write the following rules and properties for matrix multiplication.

The product of two matrices A and B is defined if the number of columns of A is equal to the number of rows of B.
If AB is defined, then BA need not be defined
If both A and B are square matrices of the same order, then both AB and BA are defined.
If AB and BA are both defined, it is not necessary that AB = BA.
If the product of two matrices is a zero matrix, it is not necessary that one of the matrices is a zero matrix.