新年坐大牢
A - Wallet Exchange
题意：共有俩钱包，每回合从其中一个钱包中拿走一块钱，谁拿走最后一块钱谁赢。
思路：奇偶讨论即可。
// Problem: A. Wallet Exchange
// Contest: Codeforces - Hello 2024
// URL: https://codeforces.com/contest/1919/problem/0
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{LL a , b;cin >> a >> b;LL t = a + b;if(t & 1){cout <<"Alice\n";} else{cout<<"Bob\n";}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
B - Plus-Minus Split
题意：给定一个"+-"串,其中"+"代表了‘’+1“,"-”代表了“-1”.你需要将整个串分成若干份，每一份的价值为子串所代表的数的绝对值,求整个串的最小价值.
思路：贪心,其实整个串的价值就是最小价值.
// Problem: B. Plus-Minus Split
// Contest: Codeforces - Hello 2024
// URL: https://codeforces.com/contest/1919/problem/B
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;int ans = 0;string s;cin >> s;for(int i = 0 ; i < n ; i ++){if(s[i] == '+'){ans++;}else{ans--;}} cout << abs(ans) << endl;
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
C - Grouping Increases
题意：给定一个数组,要求将其分成两部分,要求每部分中元素在原数组中的相对位置不能改变,每一部分的价值为：这一部分中,前一个数小于后一个数的个数.求两部分价值之和的最小值。
思路:可以想到,由于无法改变相对顺序,我们需要从前往后的插入元素.而每一部分的最后一个元素值应当越大越好。因此我们每次插入元素只需要插入到两个部分中尾数小的那部分即可,然后再算出总共价值就是最小价值.
// Problem: C. Grouping Increases// Contest: Codeforces - Hello 2024// URL: https://codeforces.com/contest/1919/problem/C// Memory Limit: 256 MB// Time Limit: 1000 ms// // Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>using namespace std;#define LL long long#define pb push_back#define x first#define y second #define endl '\n'const LL maxn = 4e05+7;const LL N = 5e05+10;const LL mod = 1e09+7;const int inf = 0x3f3f3f3f;const LL llinf = 5e18;typedef pair<int,int>pl;priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆priority_queue<LL> ma;//大根堆LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;}LL lcm(LL a , LL b){return a / gcd(a , b) * b;}int n , m;vector<int>a(N , 0);void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}}void solve() {int rear[2] = {inf , inf};int n;cin >> n;for(int i = 0 ; i < n ; i ++){cin >> a[i];} int ans = 0;for(int i = 0 ; i < n ; i ++){int cnt = 0;for(int j = 0 ; j < 2 ; j ++){cnt += (rear[j] < a[i]);}if(cnt == 0){if(rear[0] < rear[1]){rear[0] = a[i];}else{rear[1] = a[i];}}else if(cnt == 1){if(rear[0] < a[i]){rear[1] = a[i];}else{rear[0] = a[i];}}else{if(rear[0] < rear[1]){rear[0] = a[i];}else{rear[1] = a[i];}ans++;}}cout << ans << endl;} int main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;}F1 - Wine Factory (Easy Version)
题意：
思路：由于固定了,也就是前一个水塔的水必定能全部流入后一个水塔.
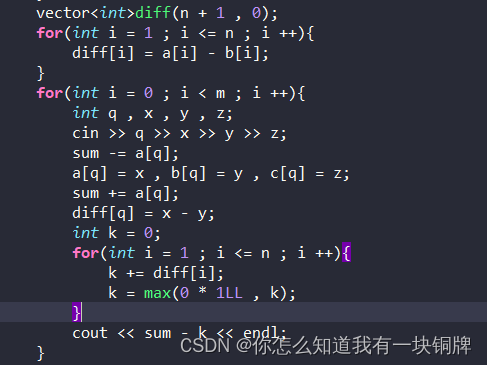
这是一开始的想法，然后发现整个过程其实是一个区间从前往后合并的过程，因此考虑用线段树去解决区间合并问题。
接下来考虑如何合并：若前面区间还有剩余的水,那么可以由后面的魔法师去变为葡萄酒，因此我们需要知道的是，区间中还剩多少水和区间中的魔法师还剩多少能量。同时我们还可以统计转换了多少葡萄酒。
每次只需要单点修改和整个区间查询就行了。
// Problem: F1. Wine Factory (Easy Version)
// Contest: Codeforces - Hello 2024
// URL: https://codeforces.com/contest/1919/problem/F1
// Memory Limit: 512 MB
// Time Limit: 5000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
#define int long long
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}
vector<int>a(N , 0);
vector<int>b(N, 0);
vector<int>c(N, 0);
struct info{LL Res;//剩余多少水LL Res_ma;//魔法师还剩余多少能量LL Value;//价值friend info operator + (info a ,info b){info c;c.Value = a.Value + b.Value;c.Res_ma = b.Res_ma + a.Res_ma;if(a.Res > 0){int d = min(a.Res , b.Res_ma);c.Res_ma -= d;c.Value += d;a.Res -= d;}c.Res = a.Res + b.Res;return c;}
};
struct node{info val;
} seg[N * 4];
struct SegTree{void update(int id){seg[id].val = seg[id * 2].val + seg[id * 2 + 1].val;}void build(int id, int l, int r){if (l == r) {seg[id].val = {max(0 * 1LL ,a[l] - b[l]) , max(0 * 1LL , b[l] - a[l]) , min(a[l] , b[l])};}else{int mid = (l + r) / 2;build(id * 2, l, mid);build(id * 2 + 1, mid + 1, r);update(id);}}void modify(int id, int l, int r, int ql, int qr){if (l == ql && r == qr){seg[id].val = {max(0 * 1LL ,a[l] - b[l]) , max(0 * 1LL , b[l] - a[l]) , min(a[l] , b[l])};return;}if (ql > r || qr < l) // 区间无交集return; // 剪枝int mid = (l + r) / 2;if (qr <= mid) modify(id * 2, l, mid, ql, qr);else if (ql > mid) modify(id * 2 + 1, mid + 1, r, ql, qr);else{modify(id * 2, l, mid, ql, mid);modify(id * 2 + 1, mid + 1, r, mid + 1, qr);}update(id);}info query(int id, int l, int r, int ql, int qr){if (ql == l && qr == r) return seg[id].val;int mid = (l + r) / 2;if (qr <= mid) return query(id * 2, l, mid, ql, qr);else if (ql > mid) return query(id * 2 + 1, mid + 1, r, ql, qr);else{return query(id * 2, l, mid, ql, mid) + query(id * 2 + 1, mid + 1, r, mid + 1, qr);}}
};
LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
void solve()
{cin >> n >> m;for(int i = 1 ; i <= n ; i ++){cin >> a[i];}for(int i = 1 ; i <= n ; i ++){cin >> b[i];}for(int i = 1 ; i < n ; i ++){cin >> c[i];}SegTree segTree;segTree.build(1 , 1 , n);for(int i = 0 ; i < m ; i ++){int q , x , y , z;cin >> q >> x >> y >> z;a[q] = x;b[q] = y;segTree.modify(1 , 1 , n , q , q);cout << segTree.query(1 , 1 , n , 1 , n).Value << endl;}
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;
// cin>>t;while(t--){solve();}return 0;
}
D - 01 Tree
题意：先有一颗未知的完整二叉树,非叶子结点的两条与子节点相连的边权一个为0，另一个为1.如今给出了根据dfs序的叶子结点的权值序列,求能否还原出一颗完整二叉树.定义结点的权值为该节点到根节点的边权之和.
思路：可以发现：同一个父亲的两个叶子结点的权值只差了1，且两个叶子结点中小的那个就是父节点的权值.也就是说，dfs序中若相邻两个数差了1，那么这两个数就是同一个父亲结点的。由此我们可以将同一个父亲的两个叶子结点中大的删除，小的保留，这样就相当于将两个叶子结点给删除了.最后若只剩下一个点没有被删除，且这个点为0，那么就代表了能够通过删除操作只保留一个顶点，反过来也就是说通过这个序列能够形成一个完整二叉树.
// Problem: D. 01 Tree
// Contest: Codeforces - Hello 2024
// URL: https://codeforces.com/contest/1919/problem/D
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 5e05+10;
const LL mod = 1e09+7;
const int inf = 0x3f3f3f3f;
const LL llinf = 5e18;
typedef pair<int,int>pl;
priority_queue<LL , vector<LL>, greater<LL> >mi;//小根堆
priority_queue<LL> ma;//大根堆
LL gcd(LL a, LL b){return b > 0 ? gcd(b , a % b) : a;
}LL lcm(LL a , LL b){return a / gcd(a , b) * b;
}
int n , m;
vector<int>a(N , 0);
void init(int n){for(int i = 0 ; i <= n ; i ++){a[i] = 0;}
}
void solve()
{cin >> n;for(int i = 1; i <= n ; i ++){cin >> a[i];}a[0] = a[n + 1] = -inf;vector<int>nex(n + 5 , 0) , pre(n + 5 , 0);for(int i = 1; i <= n ; i ++){nex[i] = i + 1;pre[i] = i - 1;}auto check = [&](int x){return (a[pre[x]] == a[x] - 1) || (a[nex[x]] == a[x] - 1);};vector<int>in(n + 5 , 0);priority_queue<pair<int,int>>ma;for(int i = 1 ; i <= n ; i ++){if(check(i)){in[i] = 1;ma.push({a[i] , i});}}while(!ma.empty()){auto tmp = ma.top();ma.pop();int pos = tmp.y;nex[pre[pos]] = nex[pos];pre[nex[pos]] = pre[pos];if(!in[nex[pos]] && check(nex[pos])){in[nex[pos]] = 1;ma.push({a[nex[pos]] , nex[pos]});}if(!in[pre[pos]] && check(pre[pos])){in[pre[pos]] = 1;ma.push({a[pre[pos]] , pre[pos]});}}int mi = n , bad = 0;for(int i = 1 ; i <= n ; i ++){bad += (!in[i]);mi = min(mi , a[i]);}if(bad == 1 && mi == 0){cout <<"YES\n";}else{cout <<"NO\n";}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cout.precision(10);int t=1;cin>>t;while(t--){solve();}return 0;
}
![[算法]使用aes进行数据加密](https://img-blog.csdnimg.cn/direct/f3826e5f058246cfb8ab7d8a2c31ca83.png)
![[MySQL] 数据库的主从复制和读写分离](https://img-blog.csdnimg.cn/direct/af2bf56486904d12a1979d0d41fb15ef.png)
