1 数学/线性代数里，其实很多东西的求得都有多种解决办法
很多概念，界定狠清晰，但是不好求
多种方法，拓宽思维
方法1：按定义直接去求解
方法2：按
2 比如求逆矩阵
概念方法，线性变化
增广矩阵
其他方法
分块矩阵
伴随矩阵
|A|=0
3 求矩阵的秩
4 求方程组的解的好方法
直接可以用行列式的方法求解啊
1.2 有没有其他方法呢？有：比如2阶行列式方法
因为二阶行列式的公式求值如下
所以二元方程组的求解也可以用行列式写成
1.3 3阶行列式
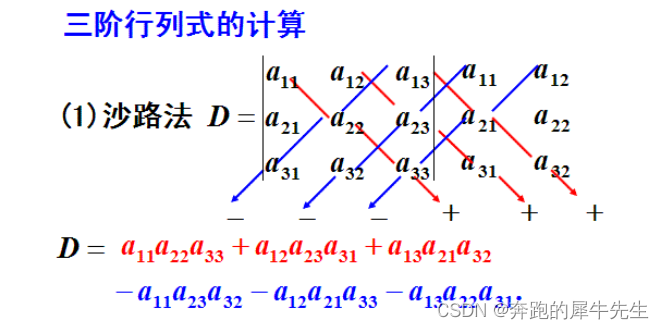
- 如果 |A|≠0 ,则，矩阵A满秩，矩阵A可逆
3.3 行列式的意义和作用呢？
- 作用1：快速解出，多元方程组的解
- 作用2：通过矩阵的余子式的转置等计算，矩阵的逆矩阵
