参考资料:用python动手学统计学
使用matplotlib.pyplot.boxplot()函数绘制箱线图
import numpy as np
import pandas as pd
from matplotlib import pyplot as pltdata_set1=np.array([2,3,3,4,4,4,4,5,5,6])
data_set2=np.array([[2,3,3,4,4,4,4,5,5,6],[5,6,6,7,7,7,7,8,8,9]])
#.T将数组data_set2由原来的2行10列转换为2列10行
data_set2=data_set2.Tplt.boxplot(data_set1)
plt.boxplot(data_set2)代码结果展示如下:


下面介绍plt.boxplot()函数中常用的几个重要参数(参数等号后为默认设置):
(1)x,表示数据源;如果是一维的数组,则直接根据数组的数据产生一个箱线图,如果是二维数组,则按列的方向对数据进行统计,即有几列数据,就做几个箱线图。
(2)notch=None,默认为False,即箱框为矩形;若设置为True的箱框沿中间向内凹陷,代表着中位数的置信区间(结合bootstrap参数学习),如下图所示:

(3)sym=None,表示对异常值的显示标记。默认显示如下。
data_set3=np.array([-5,2,3,3,4,4,4,4,5,5,6])
plt.boxplot(data_set3)
当设置为sym="b+"(b表示颜色blue,+表示标记性状)时,显示如下:

(4)vert=None,默认为True,即箱线图垂直显示;若设置为False,则箱线图水平显示,如下:
plt.boxplot(data_set1,vert=False)
(5)whis=None,设置箱线图线须的位置,默认是1.5,即1.5倍的四分位距。Q1为下四分位数,Q3为上四分位数。箱线图线须的下界值为Q1-1.5*(Q3-Q1),箱线图线须的上界值为Q3+1.5*(Q3-Q1),在上下界范围之外的数据点被认为是异常值,并标注为异常点。当数据中的最小值大于箱线图的线须的下界值时,程序会把最小值当作下界值进行作图;同样当最大值小于线须的上界值时,程序会把最大值当作上界值进行作物。图片可以参照sym参数的图来看。
(6)positions=None,表示箱线图在坐标轴上的位置,默认在坐标轴上的位置为range(1,N+1),N为数据的列数(注意range函数“包左不包右”的原则),下图注意刻度的变化:
plt.boxplot(data_set2,positions=[2,3])
(7)widths=None,表示箱子的宽度。默认设置为0.15倍间距,当设置widths=0.5时,效果如下:

(8)patch_artist=None,默认为False,即线图风格;当设置为True时,为填充风格,效果如下
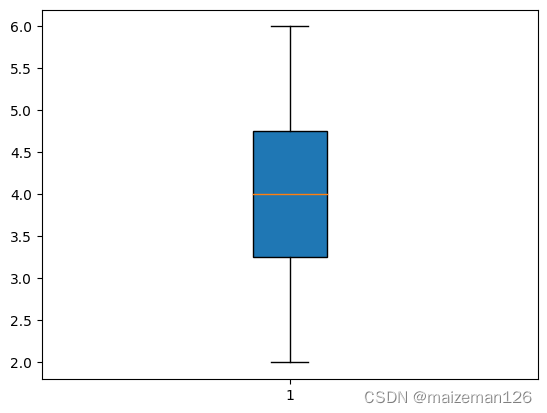
(9)bootstrap=None,当notch设置为True,用于设置对中位数的95%的置信区间的验证次数,若不对其进行设置,则默认用Gaussian-based asymptotic approximation (see McGill, R., Tukey, J.W., and Larsen, W.A., 1978, and Kendall and Stuart, 1967)对notch进行设置。bootstrap的建设设置区间为1000至10000。
plt.boxplot(data_set1,notch=True,bootstrap=1000)
(10)usermedians=None,用于指定作图的中位数,默认为None,即由程序自行计算得到;也可以自行指定中位数,下图设置为:usermedians=[3.5,7.5],展示如下,注意观察中位数所在位置的变化:
plt.boxplot(data_set2,usermedians=[3.5,7.5])
(11)conf_intervals=None,当notch设置为True时,用于设置置信区间;默认为None,即用bootstrap的相关数设置。下图表示将中位数的置信区间设置分别设置在3-5之间和3.5-4.5之间,注意观察区别。
plt.boxplot(data_set1,notch=True,conf_intervals=[(3,5)])
plt.boxplot(data_set1,notch=True,conf_intervals=[(3.5,4.5)])
(12)showmeans=None,表示是否显示均值,默认不显示。当设置为True则显示均值。
data_set3=np.array([1,2,3,3,4,4,4,4,5,9,9,10])
plt.boxplot(data_set3,showmeans=True)
(13)meanline=None,表示是否显示均值线,默认为False。当showmeans设置为True,且meanline=True时,则均值点显示为均值线。
下图为meanline=False,即默认设置的显示图片:
data_set3=np.array([1,2,3,3,4,4,4,4,5,9,9,10])
plt.boxplot(data_set3)
下图为showmeans和meanline均为True的形式
data_set3=np.array([1,2,3,3,4,4,4,4,5,9,9,10])
plt.boxplot(data_set3,showmeans=True,meanline=True)
(14)showcaps=None,默认为True,用于设置须线两头的横杠,下图设置为False注意观察变化。
plt.boxplot(data_set3,showcaps=False)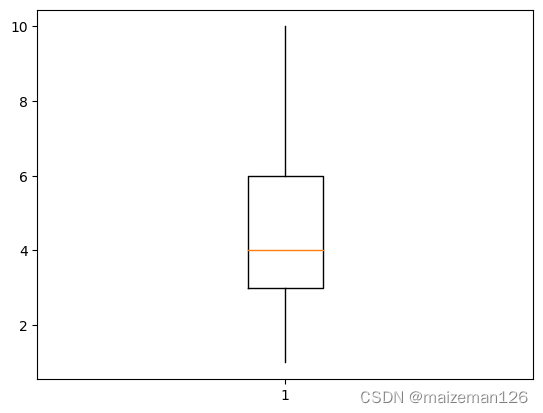
(15)showbox=None,用于设置是否显示箱线图的箱子,默认为True,下图为False时的设置:
plt.boxplot(data_set3,showbox=False)
(16)若要将刻度线处的数字改为名称,需进行如下设置:
plt.boxplot(data_set2)
plt.xticks(ticks=[1,2],labels=["x","y"])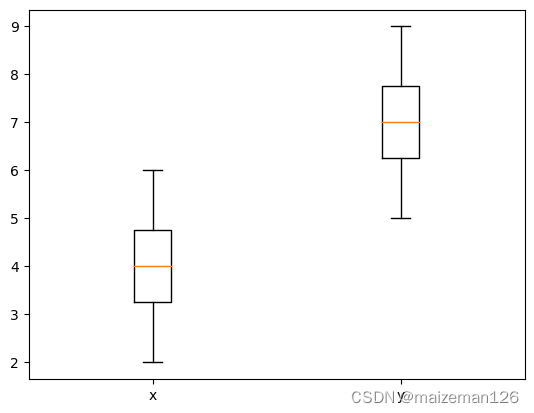


 D. Array Collapse(单调栈+dp))





真题解析)










