状态机dp概述
当一个事件涉及的过程的考虑并且方案数的考虑比较繁琐时，我们可以尝试用状态机的思想去考虑这个问题，将这个问题简化，就是去考虑一个对象他所具有的几种状态。
状态机主要考虑一下两个方面：状态和转移
状态其实也就是正常在dp过程中分析的，不用过多解释了。
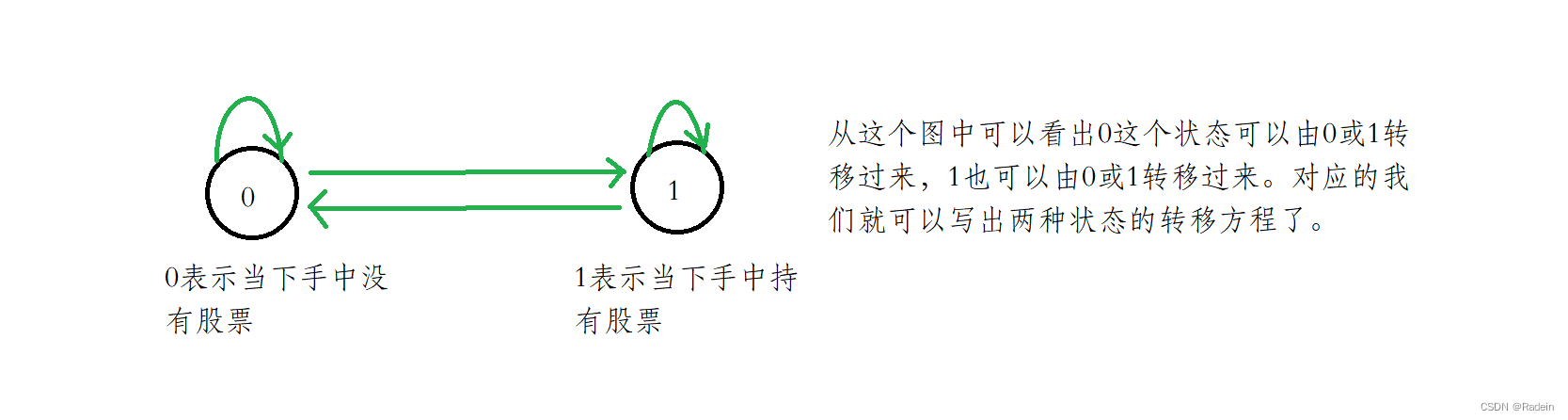
转移：状态与状态之间的转移，根据实际题目，分析状态与状态之间是否能转移，能转移的就画一根箭头。最后会发现其实就是一个有向图。
触发机制
样题：股票买卖IV
状态含义:f[i, j, 0]表示前i个股票，已经进行完j次交易，且手中没有买入时的最大收益；
f[i, j, 1]表示前i个股票，已经进行完 j - 1次交易，且已经买入第j个股票但还没卖出时的最大收益。
关于初始化：因为在最开始，我们任何一笔交易都没有产生，并且手中也没有任何股票，也就不能个进行卖出的操作。所以我们第一次操作就是从0变到1（买入股票）或继续保持0（不买股票）。所以我们直接将f[ i ][ 0 ][ 0 ]初始化为0。这样就完成了每个数据点的初始化，避免了不合法的方案进行转换。
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;
const int N = 100010, M = 110;
int f[N][M][2];
int n, k;
int w[N];int main()
{cin>>n>>k;for(int i = 1; i <=n; i ++) cin>>w[i];memset(f, -0x3f, sizeof f);for(int i = 0; i <= n; i ++) f[i][0][0] = 0;for(int i = 1; i <= n; i ++){for(int j = 1; j <= k; j ++){f[i][j][0] = max(f[i-1][j][1] + w[i], f[i - 1][j][0]);f[i][j][1] = max(f[i - 1][j][1], f[i-1][j-1][0] - w[i]);}}int res = 0;for(int i = 0; i <= k; i ++){res = max(res, f[n][i][0]);}cout<<res;
}样题2：股票买卖V
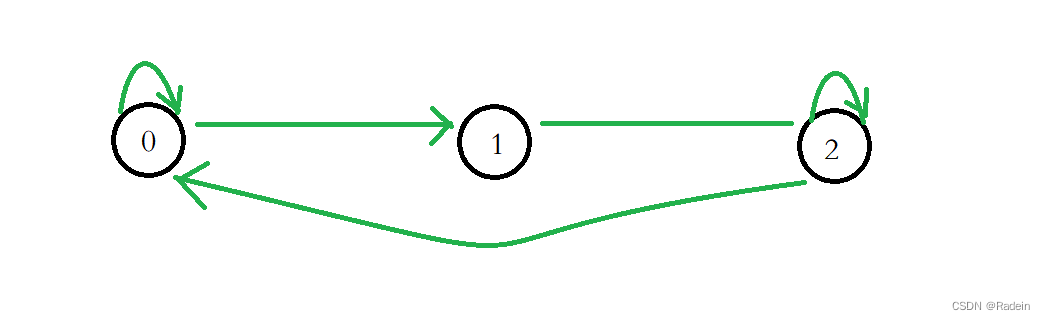
思考：这题和上面那题最大不同就是，这里可以进行无限多次交易，同时多了一个状态。这一题中共有三个状态：手中持有股票，刚刚卖出股票那一天，卖出股票天数大于等于2天。
状态转移的分析过程就和上一题思路类似。照着图把转移方程写出来。
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;
const int N = 100010;
int f[N][3];
int n;
int w[N];int main()
{cin>>n;for(int i = 1; i <= n; i ++) cin>>w[i];memset(f, -0x3f, sizeof f);f[0][2] = 0;for(int i = 1; i <= n; i ++){f[i][0] = max(f[i-1][0], f[i - 1][2] - w[i]);f[i][1] = f[i-1][0] + w[i];f[i][2] = max(f[i-1][1], f[i-1][2]);}cout<<max(f[n][1],f[n][2]);
}
