【算法每日一练]-图论（保姆级教程篇14 ）#会议（模板题） #医院设置 #虫洞 #无序字母对 #旅行计划 #最优贸易

今日知识点：

求数的重心先dfs出d[1]和cnt[i]，然后从1进行dp求解所有d[i]

两两点配对的建图方式，检查是否有环

无向图欧拉路径+路径输出

topo+dp求以i为终点的游览城市数

建立分层图转化盈利问题成求最长路

会议（模板题）

医院设置

虫洞

无序字母对

旅行计划

最优贸易

会议（模板题）

思路：

补充：首先，阅读题目可以看出来，这道题目实际上就是求树的重心。

树的重心：找到一个点，其所有的子树中最大的子树节点数最少，那么这个点就是这棵树的重心，删去重心后，达到的效果是生成的多棵树尽可能平衡。

啊？不是n-1边n点的无向图吗？怎么就一定是棵树了呢？万一是“X”型或者“米”型的无向图呢~~，哈哈我可太聪明了。~~

你直接从任意一个点做根开始，然后把该点其余的分支点都掰到下面去。也就是说把其余的子树都扭动到下面去，这不就是一颗树了吗。明白了吗！

OK，怎么解这道题呢？

举个例子：

我们不妨设置d[i]表示以此点为根的所有点总距离和，cnt[i]表示以此为根的节点数

我们首先知道d[1]=16,cnt[1]=10我们来看d[2]应该怎么求,我们发现相对于d[1]来说，如果设2为最佳点,2,5,6其距离-1，剩下的1,4,3,7,8,9,10到其距离+1。

故：d[2]=d[1] - 3 + 7 =20

其中3是子根2对应的节点数cnt[2]，7是1为子根对应的节点数cnt[1]-cnt[2]

得：d[i]=d[fa]-cnt[i]+(cnt[1]-cnt[i])

那么只需要先dfs求出来d[1]和每个点的cnt[i]。然后就可以进行dp最终求出所有点的d[i]。

#include <bits/stdc++.h>
using namespace std;
const int N=50005;
int minn=0x3f3f3f3f,ans,n,d[N],cnt[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){//一定别走fa回去cnt[u]++;//先加上自己for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;dfs(v,u,len+1);//先求孩子的cnt，之后求自己cntcnt[u]+=cnt[v];}d[1]+=len;//最后求d[1]
}
void dp(int u,int fa){for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;d[v]=d[u]-2*cnt[v]+cnt[1];dp(v,u);//这里对自己进行转移更新，再对孩子的更新}
}
int main(){cin>>n;int a,b;for(int i=1;i<n;i++){cin>>a>>b;ve[a].push_back(b);ve[b].push_back(a);}dfs(1,0,0);dp(1,0);for(int i=1;i<=n;i++){if(d[i]<minn)minn=d[i],ans=i;}cout<<ans<<" "<<minn;
}

上面我打注释的地方一定要理解

医院设置

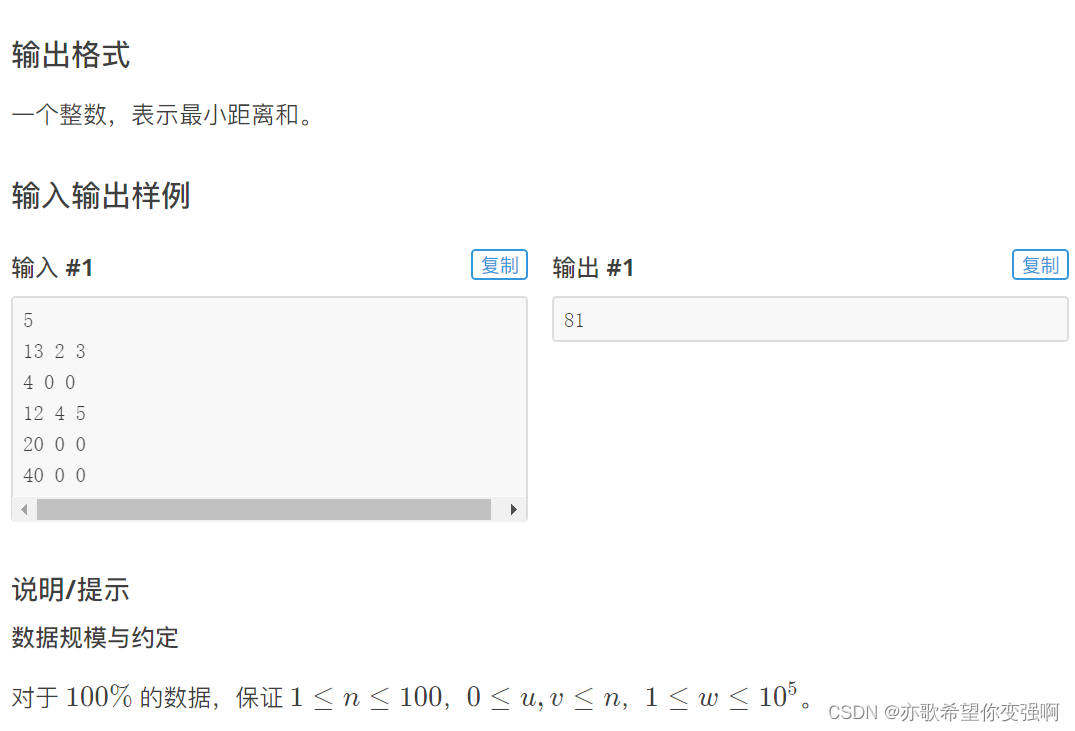
思路：

还是一道求树的重心题。不过是每个点都有一个权值。那么把权值当成“另一个世界的节点数”就好了。然后不断求cnt，之后dp就行。

#include <bits/stdc++.h>
using namespace std;
const int N=500;
int ans=0x3f3f3f3f,n,d[N],cnt[N],w[N];
vector<int>ve[N];
void dfs(int u,int fa,int len){cnt[u]=w[u];//这里还是先加自己for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;dfs(v,u,len+1);cnt[u]+=cnt[v];}d[1]+=len*w[u];//更新d[1]也要变一下
}
void dp(int u,int fa){for(int i=0;i<ve[u].size();i++){int v=ve[u][i];if(v==fa)continue;d[v]=d[u]+cnt[1]-cnt[v]*2;dp(v,u);}ans=min(ans,d[u]);
}
int main(){cin>>n;int c,a,b;for(int i=1;i<=n;i++){cin>>c>>a>>b;w[i]=c;//注意输入方式if(a)ve[i].push_back(a),ve[a].push_back(i);if(b)ve[i].push_back(b),ve[b].push_back(i);}dfs(1,0,0);dp(1,0);cout<<ans;
}

虫洞

思路：
首先分析一下：第一是如何去建图，其次是如何找方案

找方案的话就直接暴力配对吧(题上的数据量不大，肯定要暴力)，然后就是建图要保证即要方便图的还原（因为配对后还要回溯呢），又要方便跑图（每次建好都要跑一次看看是否存在一个循环），最后就是坐标范围非常大啊，所以要巧妙一点。

首先：我们对这些黑洞位置排序，只关注同行的，同行中能从A黑洞走到B黑洞的就标记一下A能到B(使用唯一的ID号映射)。

之后：dfs选择配对方案，然后dfs的for函数也是很巧妙：首先要保证不能和前面重复（相当于1号黑洞可以找2，3，4，但是之后4号一定不能再找1，2，3了，所以要保证递增）然后是g[i]=k;g[k]=i这样建图（因为是两两配对，所以每个起点最多只有一个尾点）。最后是建好图后直接从每个黑洞ID号为起点进行查询即可。

最后是检查函数cycle：从起点一直走，走到走过的就可以停止了

#include <bits/stdc++.h>
using namespace std;
int ans,n,to[20],vis[20],g[20];
struct node{int x,y;}p[20];bool cmp(node a,node b){return (a.y<b.y)||(a.y==b.y&&a.x<b.x);
}int cycle(int x){while(to[x]){//走到下一个黑洞，如果有的话if(vis[x])return 1;vis[x]=1;x=g[to[x]];//终点变成起点（如果有的话）}return 0;
}
void dfs(int k){if(k>n){int f=0;for(int i=1;i<=n;i++){//巧妙3：直接从黑洞号开始就行memset(vis,0,sizeof(vis));f|=cycle(i);//巧妙4：这里之所以这么写，是为了防止被标记过1后又被0覆盖掉}ans+=f;return ;}if(g[k])dfs(k+1);else {for(int i=k+1;i<=n;i++){//巧妙1：去重if(g[i])continue;g[i]=k;g[k]=i;//巧妙2：设置两个黑洞的关系dfs(k+1);g[i]=g[k]=0;//清除两个黑洞之间的关系}}
}
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>p[i].x>>p[i].y;sort(p+1,p+1+n,cmp);for(int i=1;i<=n-1;i++){if(p[i].y==p[i+1].y) to[i]=i+1;//把相邻且在同一航 行的标记在一起}dfs(1);cout<<ans;}

首先是方案配对，然后是建图策略(至多两两配对)，最后到检查循环都是非常精妙的，值得细看

无序字母对

思路：

这里就可以发现实际上就是在找欧拉路，首先每个字符就是代表的图中的某一个点，底下输入的字符串
就代表两点之间有连通，构造字符串就是在找输出一笔画回路，明白这个代码就很简单了

下面是代码：基于无向图得欧拉路径问题+路径输出

无向图得欧拉路径：连通图，且没有度为奇数的节点(欧拉回路) 或只有两个2个度为奇数的节点

#include <bits/stdc++.h>
using namespace std;
const int N=300;
int g[N][N],fa[N],du[N],m;
char ans[N*N],s[N];
int find(int x)
{if(x!=fa[x]) fa[x]=find(fa[x]);return fa[x];//返回祖先 
}void dfs(int x){for(int i=0;i<N;i++)if(g[x][i]){g[x][i]=g[i][x]=0;//取过了这个字母就情空，避免走环 g=0相当于vis=1dfs(i);}ans[m--]=x;
}int main()
{cin>>m;for(int i=0; i<N; i++) fa[i]=i;for(int i=1; i<=m; i++){scanf("%s",s);g[s[0]][s[1]]=g[s[1]][s[0]]=1;du[s[0]]++;du[s[1]]++;int f1=find(s[0]),f2=find(s[1]);//合并建树fa[f1]=f2;}
//判断是否连通int tmp=0;for(int i=0;i<N;i++)if(fa[i]==i&&du[i])tmp++;if(tmp!=1){cout<<"No Solution";return 0;}
//是否存在欧拉路径	int f=0,rt=0;for(int i=0;i<N;i++){if(du[i]&1){f++;	//一边统计多少个奇数度点，一边找奇数的rt做起点if(!rt)rt=i;}}if(f&&f!=2){cout<<"No Solution";return 0;}
//按照字典序最小开始输出路径if(!rt){//rt不能从0开始for(int i=0;i<N;i++){//按照ASCII找最小的起点rtif(du[i]){rt=i;break;}}}dfs(rt);cout<<ans;}

旅行计划

思路：

题上问以i点为终点的最多游览的城市数。非常类似之前说过的“食物链计数”那道题。

设置f[i]表示以i为终点的最多的游览城市数。那么从入度为0的点开始进行正向topo即可。

顺便再补充一个方向：如果设置f[i]表示以i为起点的最多的游览城市数。那么肯定不能正向topo。

这个时候需要用dfs进行回溯式topo处理。

#include<bits/stdc++.h> 
using namespace std;
const int N=100005;
vector <int>ve[N];
queue<int> q;
int n,m,ans,f[N],in[N],out[N];int main(){cin>>n>>m;int x,y;for(int i=1;i<=m;i++){cin>>x>>y;ve[x].push_back(y);in[y]++;out[x]++;}for(int i=1;i<=n;i++){if(in[i]==0){q.push(i);f[i]=1;}}while(q.size()){//进行拓扑排序int cur=q.front();q.pop();for(int i=0,sz=ve[cur].size();i<sz;i++){int v=ve[cur][i];f[v]=f[cur]+1;in[v]--;if(in[v]==0) q.push(v);}		}for(int i=1;i<=n;i++)cout<<f[i]<<'\n';return 0;
}

最优贸易

思路：

每个点都可以不卖不买，买，或卖这3种状态，那么分层图自然最合适。

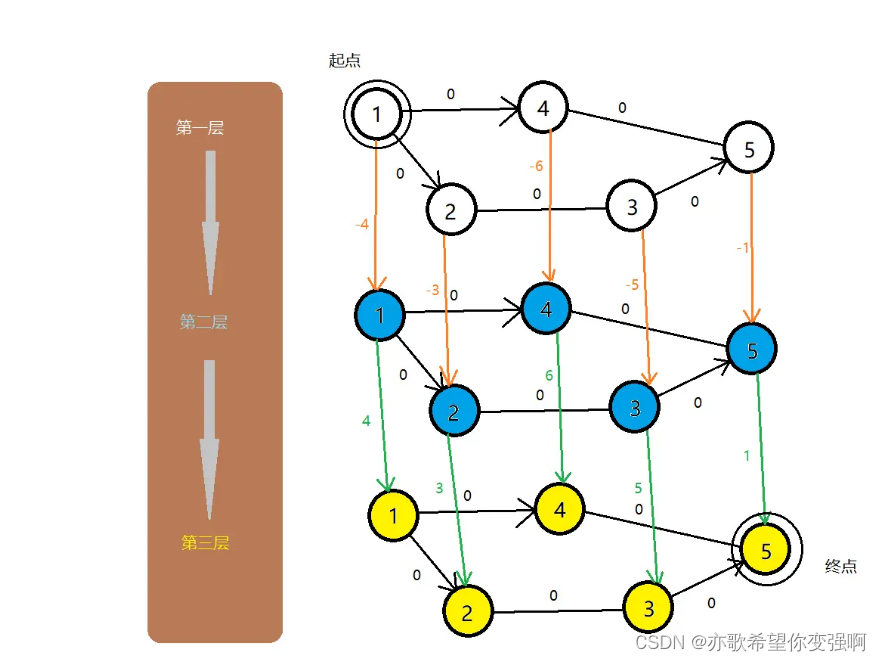
最上面的层之间不论怎么跑动一定不会赚钱或亏钱。只有在层之间移动才能赚钱或亏钱。

也就是层内关系权值为0，层间非0.

然后就转化成spfa求最长路即可。

#include <bits/stdc++.h> 
using namespace std;
const int N=1e5+5;
int cnt,head[N*3];
int dis[N*3];
bool vis[N*3];
struct Edge{ int to,w,next;}e[250000*3];
void add(int u,int v,int w) { e[++cnt]=(Edge){v,w,head[u]}; head[u]=cnt;}
void spfa(int s)
{memset(dis,-0x3f,sizeof(dis));queue<int>Q;dis[s]=0;vis[s]=1;Q.push(s);while(!Q.empty()){int u=Q.front(); Q.pop();vis[u]=0;for(int i=head[u];i;i=e[i].next){int v=e[i].to,w=e[i].w;if(dis[v]<dis[u]+w) {dis[v]=dis[u]+w;if(vis[v])continue;Q.push(v);vis[v]=1;	}}}    
}int main()
{int n,m,price;cin>>n>>m; for(int i=1;i<=n;i++){cin>>price;add(i,i+n,-price);//在层之间建立关系add(i+n,i+n*2,price);}int u,v,c;for(int i=0;i<m;++i){cin>>u>>v>>c;add(u,v,0);add(u+n,v+n,0);add(u+2*n,v+2*n,0);//建立 分层图（层内图）if(c==2){add(v,u,0);add(v+n,u+n,0);add(v+2*n,u+2*n,0);}}spfa(1);printf("%d",dis[n+2*n]);return 0;
}

然后做完这道题，可以很明显发现和之前做过的“飞行路线”一题很像。那道题中是层内关系的权值非0，层间的关系权值为0，最后在最下面的层找答案即可。本题刚好反过来。