3D数学基础

矢量/向量

在笔记中

• 变量使用小写字母表示，a
• 由于笔记中画上箭头表示向量比较麻烦，这里小写字母加粗显示，a
• 矩阵变量使用粗体大写字母表示，A

概述 - 什么是向量

在线性代数中，Vector被称为向量。在几何中，Vector被称为矢量。

向量意义
对数学家来说，向量是一个数字列表(程序员一般称为数组)。

[1,2,3]表示为行向量，垂直过来就是列向量。可以引用向量来表示各个分量，通常使用x,y来代指二维向量中的元素，x,y,z来代指三维向量中的元素。比如a=[1,2,3]中ax=1,ay=2,az=3

矢量意义

矢量是具有大小和方向的有向线段

• 矢量的大小：矢量的长度，非负值。
• 矢量的方向：描述矢量在空间中指向的方向。

图形上每个矢量是位置无关的，比如使用笛卡尔坐标描述矢量时，每个坐标相当于描述对应维度(x、y或其他)中有符号位移。
比如三维矢量[3,-1,2]可以表示为①向+x轴平移3个单位②向+y轴平移-1个单位(或者-y轴平移1个单位)③向+z轴平移2个单位。其实顺序不重要，移动的总量是一样的。

零矢量：矢量中唯一没有方向的，可以理解为无位移(而不是一个点因为矢量不描述一点)

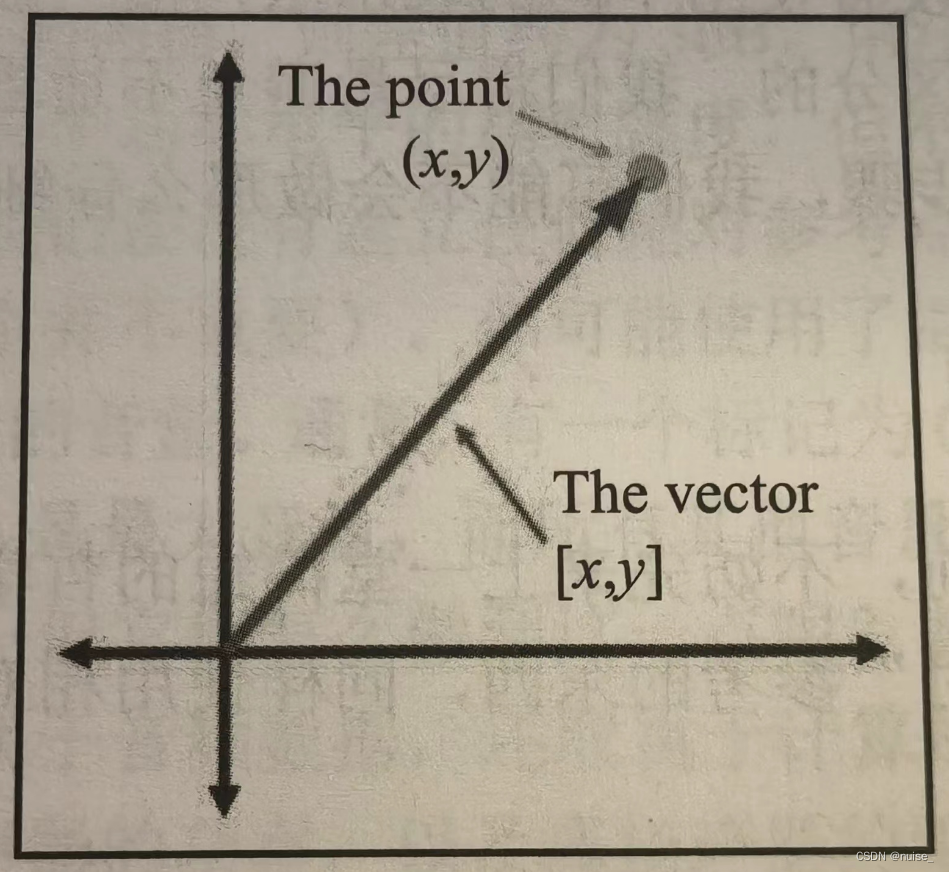
点与矢量的关系
假设有点(x,y)与矢量[x,y]
如果从原点开始按照矢量[x,y]指定的量移动，最终将到达点(x,y)的位置。或者说矢量[x,y]给出了原点到点(x,y)的位移。

单位矢量：只关注方向不关注大小

单位矢量/归一化矢量 表示大小为1(单位长度)的矢量

有时会将单位向量称为法线，法线通常隐含垂直于其他东西的矢量,主要关注点在垂直而不是单位长度。法线往往是单位向量，但是也有例外(所以需要注意例外的情况)

总结

• 归一化矢量是大小为单位长度的矢量
• 法线与某些东西垂直的矢量，通常情况是单位长度

计算公式
v的单位矢量=v/|v|

矢量的长度

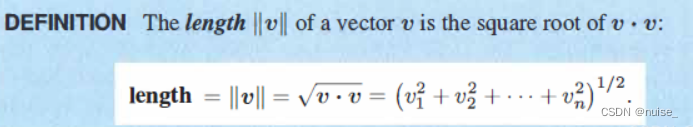
数学运算

标量和矢量的乘法，标量乘以矢量的每个分量
k[x,y,z] = [x,y,z]k = [kx,ky,kz]

矢量的加法与减法

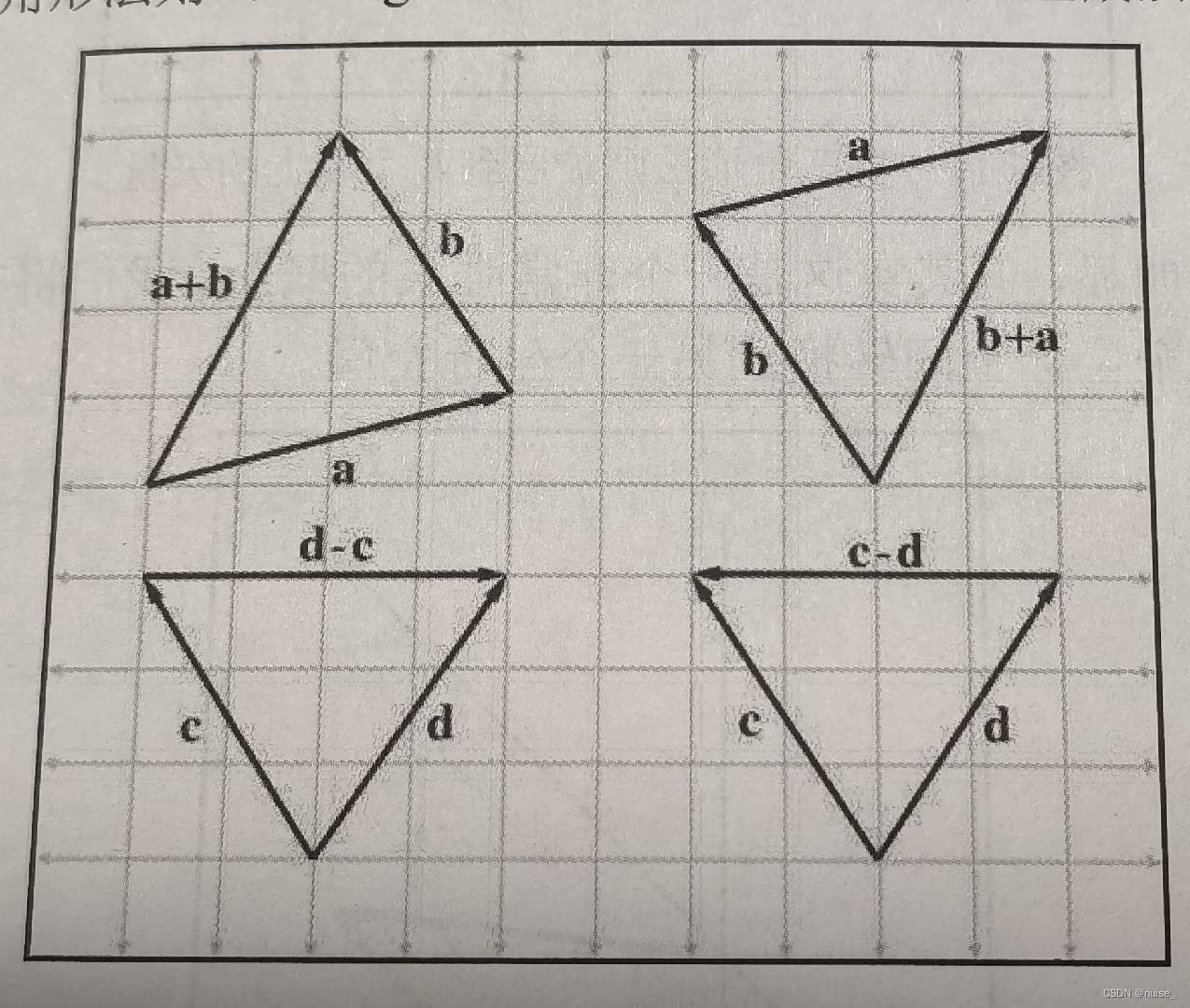
规则：相应分量相加/相减

a+b= b+a
a-b = -(b-a)

比如a+b，三角形法则几何理解为从一个点开始应用由a指定的位移，然后再应用由b指定的位移

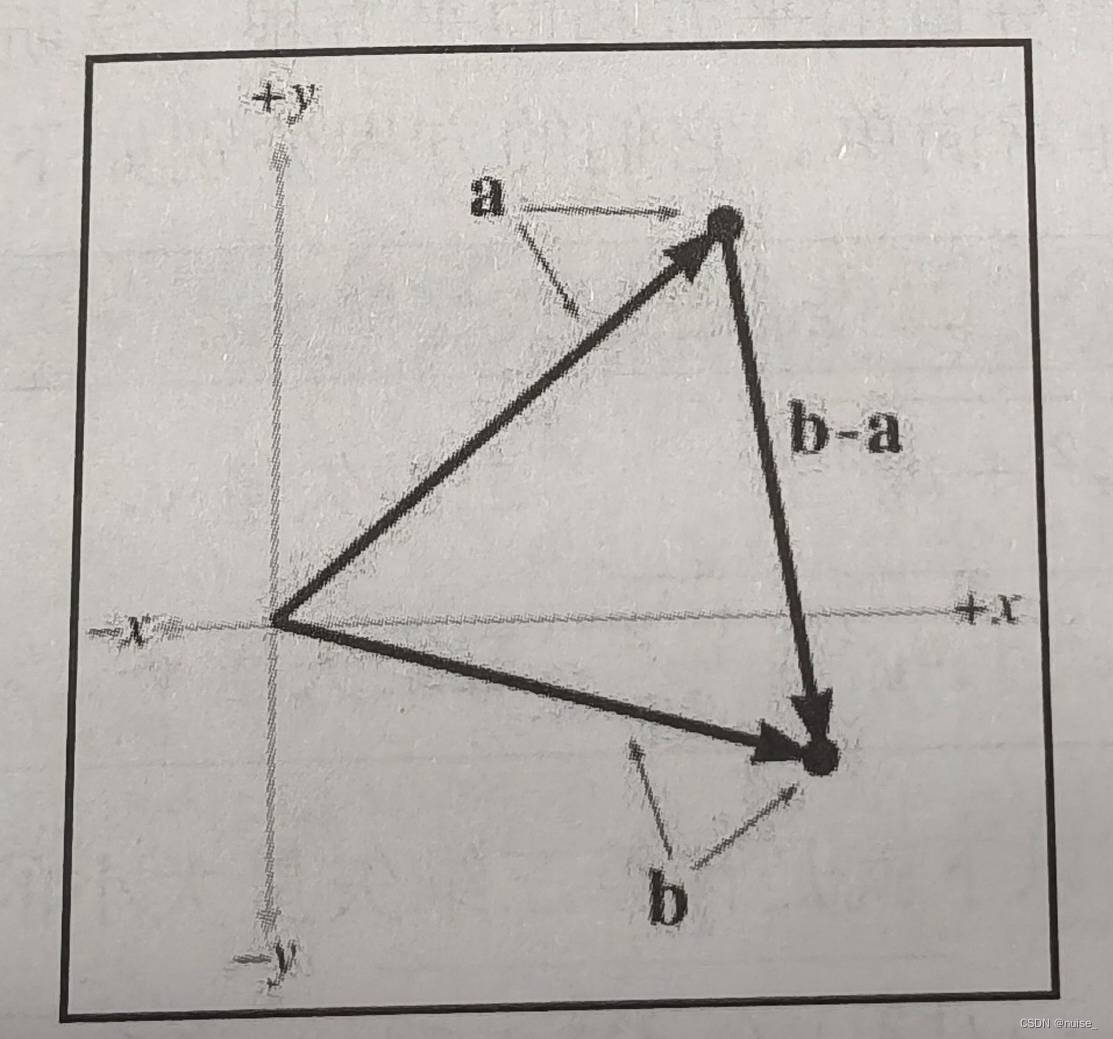
减法的几何意义计算一个点到另一个点的位移

比如a点到b的距离，将ab理解为来自原点的矢量，b-a产生的是从a到b的矢量，矢量b-a的长度就是两点之间的距离。

矢量的点积与叉积

矩阵

方阵几何意义 - 表示空间坐标的变换

• 方阵的行可以理解为坐标空间的基矢量
• 将矢量从原始空间变化到新坐标空间的方法是：矢量 * 矩阵
• 原始坐标空间到由基矢量定义的坐标空间的变化是线性变化(保留直线、平行线也保持平行、原点不移动变化不包含平移)，但角度、长度、面积等可能在变化后发生变化。
• 可通过可视化变化后坐标空间的基矢量来可视化矩阵。

组合变换 矩阵的乘法

AB: 先应用A变换，执行B变换

渲染案例
世界上任何位置和方向都有一个对象，假设希望给定的任意位置和方向上的相机渲染此对象。
前提：取得该对象的顶点很多顶点)
步骤
1.模型变换，将对象的顶点从对象空间变换到世界空间中
2.视图变换，将世界空间顶点变换到相机空间

变换的分类

映射F(a)=b 表示映射F将a映射到b

变换类型	判断标准	描述
线性变换	当F满足线性映射时,F(a+b) = F(a)+F(b) 且 F(ka) = F(kb)	将两个矢量相加然后执行变换 = 单独对两个矢量执行变换 然后将变换后的矢量加载一起。 缩放一个矢量然后执行变换 = 先变换后缩放
仿射变换	v’ =vm+b	任何线性变换都是放射变换，但并非所有仿射变换都是线性变化，仿射变换包含平移
可逆变换	执行的变换是可以撤销的，撤销之后恢复原样	找到线性变换的逆 = 找到矩阵的逆，可逆矩阵的行列式非0
保持角度的变换	两矢量之间的角度在变换后的大小或方向没有变化	平移、旋转、均匀缩放是保持角度的变换
正交变换		正交矩阵保留角度、面积和体积的大小，符合可能不一样 正交矩阵的行列式 = ± 1
刚体变换/合适变换	改变对象的位置和方向但不改变其形状 保留角度、长度、面积和体积。	刚体变换矩阵的行列式 = 1

Y表示始终关联，没有Y表示并不总是关联

矩阵的行列式

矩阵行列式的几何意义

• 在二维中，表示具有基矢量作为两条边的平行四边形或倾斜框的有符号面积。
  • 如果倾斜框相对于原始方向是翻转的，则该区域的面积为负
• 在三维中，表示平行六面体的体积，具有3个变换基矢量作为边。

矩阵的行列式，可以帮助对矩阵表示的变换类型进行分类。